4.3.1. Расчетная схема системы смазки

Упрощенная расчетная система смазки газотурбинного двигателя, которую необходимо рассчитать, показана рис.4.9. Масло из бака 1 подается насосом 12 к узлам опор, расположенных в разных местах двигателя.

К подшипникам масло подводится струйными форсунками 22, 28, 32. Особенностью системы является то, что масло обладает большой вязкостью. Поэтому скорость движения масла в трубопроводах системы смазки обычно меньше, чем в трубопроводах гидравлических систем, где рабочим телом является вода, керосин или бензин.

При расчете этой системы давление в масляном баке можно принять равным атмосферному давлению р_н на высоте полета Н. Температура масла дана в задании. Давление среды, в которой работают подшипники, можно считать равным атмосферному давлению р_н. Форсунка рассчитывается по уже изложенной методике. Масло обладает низким значением давления насыщенных паров, поэтому величина минимально допустимого давления принимается равной величине антикавитационного запаса р_мин=Δр_нп. Расчет участка всасывания маслосистемы проводится аналогично расчету участка всасывания топливной системы.

5. Порядок расчета гидравлической системы

1. Для заданной температуры определяют по справочным данным (см. приложение или работы [5, 14]) теплофизические характеристики рабочей жидкости:

- плотность жидкости ρ (кг/м );

- динамический μ (Па·с) или кинематический v (м²/с) коэффициент вязкости;

- давление насыщенных паров р_нп (Па).

Если для заданной температуры табличное значение величины отсутствует, необходимо построить по табличным значениям график нужной физической величины и по нему найти значение искомой величины для заданной температуры.

2. Для заданной высоты расположения Н гидросистемы вычисляют атмосферное давление р_н по формуле работы (6):

_,

_,

где р_н0 - атмосферное давление при Н=0.

Рис.4.9. Бланк – задание и расчетная схема системы смазки ГТД

Характеристики системы смазки Таблица 3

№ задания	Размеры трубопроводов													№ варианта		Исходные данные
	l3, м	l5, м	l7, м	l9, м	l11, м	l13, м	l15, м	l17, м	l19, l25 м	l23, м		l21, l27, l31, м				H, м м	G, кг/с	Δрф, 10-5 Па
1	0,4	0,6	1,0	1,3	1,1	0,7	1,3	0,5	0,8	1,2		1,1		1		0	0,10	3,0
2	0,5	0,8	1,2	1,0	1,3	0,9	1,1	0,6	0,9	1,3		1,0		2		500	0,11	3,1
3	1,1	1,2	1,5	0,9	1,4	1,0	0,9	0,8	0,6	1,4		1,2		3		1000	0,12	3,2
4	0,8	0,4	1,1	0,8	1,2	0,8	1,2	0,7	0,7	1,5		1,3		4		1500	0,13	3,3
5	0,6	0,7	1,0	1,1	1,4	0,7	1,1	0,4	0,8	1,6		1,1		5		2000	0,14	3,4
6	0,7	0,6	1,3	1,2	1,2	0,6	1,3	0,5	0,8	1,7		1,4		6		2500	0,15	3,5
7	0,5	0,9	0,8	0,7	1,0	1,1	0,9	0,6	'0,7	1,8		0,9		7		3000	0,16	3,6
8	0,9	1,0	0,9	0,8	0,9	1,0	1,2	0,8	0,5	1,9		1,0		8		4500	0,17	3,7
9	1,0	0,7	0,8	0,5	1,2	0,8	1,1	0,7	0,6	2,0		0,8		9		5000	0,18	3,8
10	0,3	0,4	0,7	0,6	0,9	1,2	0,8	0,6	0,7	1,9		1,0		10		5500	0,19	3,9
11	0,6	0,7	1,0	1,1	1,0	0,5	0,9	0,4	0,5	1,8		1,1		11		6000	0,20	4,0
12	0,5	0,5	1,2	0,9	0,8	0,7	1,0	0,6	0,6	1,7		1,1		12		6500	0,19	4,1
13	0,7	0,4	1,3	1,2	0,9	0,6	1,1	0,9	1,0	1,6		0,8		13		7000	0,18	4,2
14	0,3	0,3	1,1	0,7	1,5	0,6	1,2	0,7	0,4	!»5		0,7		14		7500	0,17	4,3
15	0,6	0,5	1,0	0,7	1,1	0,5	1,4	1,0	0,7	1,4		0,3		15		8000	0,16	4,4
16	0,4	0,7	0,9	1,0	1,2	0,7	0,9	1,1	0,9	1,3		1,0		16		9000	0,15	4,5
17	0,8	0,6	1,1	0,5	0,6	0,9	1,1	0,7	1,0	1,2		0,8		17		9500	0,14	4,6
18	1,1	0,9	1,0	0,7	0,5	0,4	1,0	0,9	0,6	1,1		1Д		18		10000	0,13	4,7
19	0,4	0,7	0,9	1,0	0,6	1,1	0,5	1,0	0,7	0,9		0,8		19		10500	0,12	4,8
20	1,0	0,6	0,8	1,1	0,7	1,2	0,9	1,2	0,4	0,5		1,0		20		11000	0,11	4,9
21	0,9	0,7	0,6	0,7	1,4	1,1	0,4	0,9	0,7	0,5		0,7		21		0	0,10	5,0
22	1,1	1,1	1,0	0,9	0,9	1,3	1,1	1,1	0,9	0,6		1,1		22		500	0,12	5,1
23	0,7	1,6	0,9	0,6	1,1	1,2	0,9	1,4	0,6	0,8	1,2		23		1000		0,13	5,2
24	0,8	1,4	0,7	1,2	1,4	0,7	1,0	1,6	1,2	0,6	0,9		24		1500		0,14	5,3
25	0,4	1,1	1,2	1,0	1,2	1,4	0,7	1,2	0,7	0,5		1,1		25		2000	0,15	5,4
26	0,6	0,9	1,1	0,7	0,8	1,2	1,1	0,9	1,4	0,5		1,0		26		2500	0,16	5,5
27	0,9	1,0	0,7	1,1	0,6	1,6	0,7	1,4	0,6	1,1		1,3		27		3000	0,17	5,6-
28	1,1	0,8	0,9	1,0	1,3	09	0,8	1,1	0,5	1,2		0,7		28		4500	0,18	5,7-
29	1,3	1,1	0,4	0,9	0,7	1,4	1,3	1,0	1,2	1,3		0,9		29		5000	0,19	5,8
30	0,9	1,7	1,2	1,1	0,9	1,3	1,1	1,6	0,7	1,4		1,3		30		5500	0,20	5,9
31	0,8	0,8	1,0	1,2	1,4	0,9	1,4	0,9	1,3	1,5		1,0		31		6000	0,19	6,0
32	1,0	1,2	1,1	0,8	0,9	1,3	1,1	1,1	0,8	1,6		0,9		32		6500	0,18	6,1
33	1,2	0,8	0,7	1,3	1,1	1,2	1,0	1,6	1,1	1,7		1,3		33		7000	0,17	6,2
34	0,8	0,6	0,9	1,4	1,6	0,8	0,9	1,1	1,0	1,8		0,6		34		6000	0,16	6,3

Δр_ф = р - р_Н - перепад (разность давлений) на отверстии форсунки

3. Выбирают скорость течения жидкости в трубопроводах всасывающей и_в, и напорной и_н магистралей. Рекомендуются следующие значения:

- топливопитание ВРД и_в = 2...5 м/с; и_н = 5...15 м/с;

- система смазки ВРД и_в = 0,8_...1,5 м/с; и_н = 1,5_...3 м/с;

- система дождевания и_в=2...4 м/c; и_н= 4...6 м/c.

Для ориентировки выбора значения скорости можно руковод-ствоваться требованием, что течение в трубах гидросистемы соответствует течению в гидравлически гладких трубах

4. Используя уравнение расхода (1), рассчитывают внутренний диаметр трубопроводов всасывающей d_в' и напорной d_н' магистралей:

d_в' = (м); d_н' = (м).

5. Определяют ближайший к стандартному внутренний диаметр труб всасывающей d_в и напорной магистралей d_н, выпускаемый промышленностью. Для топливопитания ВРД используются стальные трубы, для системы смазки ВРД - стальные или дюралюминиевые, для системы дождевания - стальные трубы.

Внутренний диаметр труб (в мм) из алюминия и алюминиевых сплавов по ГОСТ 18475-73 и из коррозионно-стойкой стали по ГОСТ 9940-72: от 3 до 10 мм - через 0,5 мм; от 10 до 50 мм - через 1 мм.

6. Используя уравнение расхода (1), уточняют значение скорости жидкости в реальных трубопроводах с выбранным внутренним диаметром.

и_в = (м/с); и_н = (м/с).

7. Определяют расходы жидкости, а затем ее скорости и числа Рейнольдса после разветвления магистрали. Полагаем, что расходы жидкости через каждую форсунку гидросистемы должен быть одинаков.

Так как диаметр всех трубопроводов напорной магистрали одинаков, то, во сколько раз изменился расход жидкости после тройника, во столько же раз изменится скорость течения жидкости, а также и число Рейнольдса

8. Вычисляют значения ρgz и для входа (индекс 1) и выхода (индекс 2) каждого гидравлического элемента и заносят в таблицу.

9. Определяют коэффициенты путевых потерь на всех участках гидравлической системы, считая трубы гидравлически гладкими (при Re≤ 2300 режим считать ламинарным, при Rе > 2300 режим считать турбулентным).

10. Определяют путевые потери в трубопроводах по формуле Дарси. Условимся величину путевых потерь полного давления обозначать с двумя нижними индексами. Первый индекс - это буква l, а второй - номер трубопровода, например, Δр_l1 для системы дождевания, Δр_l4 для топливной системы, Δр_l3 - для первого трубопровода системы смазки.

11. Вычисляют потери полного давления в местных сопротивлениях по формуле Вейсбаха. Коэффициенты гидравлического сопротивления для разных видов местных сопротивлений приведены в Приложении или в задании. (Считать, что все форсунки данной системы имеют одинаковую геометрию). Расчет фильтра сводится к определению потерь при течении через металлическую сетку и потерь давления при внезапном расширении и сужении. Условимся величину местных потерь полного давления обозначать с одним нижним индексом - номером местного сопротивления. Например, для входного фильтра дождевальной системы потери давления будем обозначать Δр₂, для линейных фильтров всех рассмотренных систем - Δр₆, Δр₈, Δр₁₈ соответственно.

15. Рассчитывают распределение статического давления во всасывающей магистрали. Расчет рекомендуется проводить в несколько этапов.

На первом этапе при заданных условиях работы гидросистемы вычисляется давление на входе в насос. Для этого записывается уравнение Бернулли для участка всасывания, ограниченного сечениями 1-1, совпадающим со свободной поверхностью жидкости в баке (бассейне) и 2-2, расположенного в сечении вход в насос:

. (30)

Граничные условия для этого уравнения:

z₁ - высота положения свободной поверхности жидкости относительно нивелирной плоскости. Она определяется в соответствии с заданием. Нивелирную плоскость рекомендуется располагать так, чтобы ни один элемент участка всасывания не располагался ниже нее;

р₁ - давление на свободной поверхности жидкости. Оно равно р₁=р_Н;

u₁ - скорость жидкости на свободной поверхности. Так как размеры бака (бассейна) много больше диаметра трубопровода, то в соответствии с уравнением неразрывности можно принять u₁=0.

z₂ - высота положения сечения входа в насос. Она определяется в соответствии с заданием;

р₂ - давление на входе в насос. Его нужно определить;

u₂ - скорость жидкости на входе в насос. Она определена в п.6 и равна u₂= u_в;

α₂ - коэффициент Кориолиса в магистрали всасывания. Для ламинарного режима течения α₂=2, для турбулентного - α₂=1;

ΣΔр_li - сумма потерь давления на всех i трубопроводах участка всасывания;

∑Δр_мj - сумма потерь давления на всех j местных сопротивлениях участка всасывания.

Подставляя значения граничных условий в уравнение Бернулли (30), получаем уравнение

, (31)

в котором только одна неизвестная величина, подлежащая определению - давление на входе в насос р₂.

Вычислив значение р₂, сравниваем его со значением минимально допустимого давления р_мин=р_нп+Δр_нп с целью выяснения необходимости установки подкачивающего насоса и наддува бака, а также снабжения дождевальной установки промежуточным баком

Если подкачивающий насос установить необходимо, то давление, которое он должен создавать определяется также с помощью уравнения Бернулли (30) с такими граничными условиями. Сечение 1-1 располагаем на выходе подкачивающего насоса, который крепится к баку. Поэтому граничные условия:

z₁ - высота положения выходного сечения подкачивающего насоса. Ввиду малых размеров насоса положение его выходного сечения полагаем совпадающим с положением свободной поверхности жидкости в баке;

р₁ - давление на выходе из подкачивающего насоса. Оно подлежит определению;

u₁ - скорость жидкости на выходе подкачивающего насоса. Она равна скорости жидкости в участке всасывания, т.е. u₁=u_в;

z₂ - высота положения сечения входа в основной насос;

u₂ - скорость жидкости на входе в насос. Она определена в п.6 и равна u₂= u_в;

р₂=р_мин= р_нп+Δр_нп - давление на входе в основной насос;

ΣΔр_li - сумма потерь давления на всех i трубопроводах участка всасывания;

∑Δр_мj - сумма потерь давления на всех j местных сопротивлениях участка всасывания за исключением потерь давления на входе в трубопровод для топливной и масляной систем, а для дождевальной установки - за исключением потерь давления на входном фильтре. Установка подкачивающего (погружного) насоса в дождевальной гидросистеме требует установки промежуточного бака. Поэтому появляются потери на внезапное расширение и внезапное сужение с коэффициентами местных потерь на внезапное расширение ζ_вр=1 и на внезапное сужение ζ_вс=0,5. После подстановки граничных условий в уравнение (30) получаем уравнение

,

позволяющее вычислить требуемое давление на выходе из подкачивающего насоса р₁.

На втором этапе проводится проверка работоспособности подкачивающего насоса в заданных высотных условиях: записывается уравнение Бернулли для участка системы, ограниченного свободной поверхностью жидкости в баке и входным сечением подкачивающего насоса. Для рассматриваемого участка граничные условия таковы.

Сечение 1-1:

z₁ - высота положения свободной поверхности жидкости относительно нивелирной плоскости;

р₁ = р_Н - давление на свободной поверхности жидкости. Оно равно р₁=р_Н;

u₁ - скорость жидкости на свободной поверхности. Так как размеры бака (бассейна) много больше диаметра трубопровода, то в соответствии с уравнением неразрывности можно принять u₁=0.

Сечение 2-2:

z₂ = z₁- высота положения сечения входа в подкачивающий насос;

u₂ = u_в - скорость жидкости на входе в подкачивающий насос;

р₂ - давление на входе в подкачивающий насос - подлежит определению;

ΣΔр_li = 0, т.к. трубопроводы до входа в подкачивающий насос отсутствуют (не устанавливаются);

∑Δр_мj = Δр_вх - т.к. на расчетном участке имеется только одно местное сопротивление - сопротивление входа в трубопровод.

После подстановки граничных условий в уравнение Бернулли (30) получаем:

.

Из этого уравнения следует, что давление на входе подкачивающего насоса меньше давления на свободной поверхности жидкости в баке на величину динамического давления ρu²_в/2 и на величину гидравлических потерь давления на входе в трубопровод, т.е.

.

Если давление р₂ ≥ р_мин, то в заданных условиях подкачивающий насос работает нормально, без кавитации, и ничего для обеспечения его нормальной работы предпринимать не нужно.

Если же р₂ < р_мин, то атмосферное давление не обеспечивает нормальную работу подкачивающего насоса. Для обеспечения безкавитационной работы подкачивающего насоса в бак подается от внешнего источника (компрессора) воздух с давлением

.

Разность давления воздуха, подаваемого в бак, и давления воздуха в атмосфере называется давлением наддува бака:

р_б - р_Н = Δр_нд.

После определения значений давления в начале и конце участка всасывания наступает очередь третьего этапа расчета распределения давления по характерным его сечениям.

Так как местные сопротивления, по их определению, не имеют длины, за номер характерного сечения в системе будем принимать номер местного сопротивления. В местном сопротивлении давление изменяется скачком, а на трубопроводах, разделяющих местные сопротивления - линейно.

Поскольку значения давлений в баке, на входе и на выходе подкачивающего насоса (если он установлен) определены на первых двух этапах, то расчет значений давления в характерных сечениях гидросистемы начинаем с определения давления на выходе первого после подкачивающего насоса трубопровода (давление на входе в этот трубопровод равно давлению на выходе из подкачивающего насоса).

Записав уравнение Бернулли для начального и конечного сечений трубопровода и подставив в него граничные условия (значения высот положения сечений z₁ и z₂, скорости на входе и выходе из трубопровода, давления на входе в трубопровод) и значения путевых потерь в этом трубопроводе, можно вычислить давление в выходном сечении. Значение этого давления будет являться значением давления на входе в местное сопротивление. подсоединенное к трубопроводу

Применив уравнение Бернулли для входного и выходного сечений местного сопротивления, присоединенного к трубопроводу, с подстановкой граничных условий и потерь давления на рассматриваемом сопротивлении, определяем давление на выходе из него. При подстановке граничных условий не следует забывать, что длина местного сопротивления равна нулю.

Рассмотренную процедуру определения давлений на выходе каждого начального элемента гидросистемы (путевого и местного) применяем ко всем остальным элементам участка всасывания. Контролем правильности расчета всех характеристик течения на участке всасывания будет равенство давления на выходе последнего элемента гидросистемы участка всасывания давлению на входе в основной насос.

Обобщая процедуру определения давления в каждом сечении участка всасывания, можно сказать: для произвольного i-го элемента гидравлической системы в предположении, что коэффициенты Кориолиса в сечениях входа и выхода одинаковы, уравнение Бернулли имеет вид:

ρgz_i + р_i + = ρgz_i+1 + р_i+1 + + р_r (Па),

где

i - номер входного сечения i-го элемента гидросистемы;

i+1 - номер следующего по течению сечения (выходного) i-го элемента гидросистемы.

Для горизонтального участка трубопровода или для местного сопротивления z_i= z_i+1. Следовательно, давление на входе в элемент:

р_i = р_i+1 + - + р. (Па).

Если при этом скорости жидкости u_i и u_i+1 одинаковы, то

р_i = р_i+1 + р_r (Па).

Если трубопровод расположен вертикально, то

р_i = р_i+1+ ρg(z_i+1-z_i) + р_r (Па).

Полученные значения давления для входа (индекс 1) и выхода (индекс 2) каждого элемента заносят в таблицу.

16. Рассчитываем участок нагнетания. Для упрощения расчета примем, что участок нагнетания после разветвления в тройниках 8 дождевальной системы, 20 систем топливопитания и смазки расположен горизонтально на высоте указанных тройников. Такое упрощение можно принять, так как изменение энергии положения жидкости на этих участках много меньше потерь давления на путевых и местных сопротивлениях. Определяем давление на выходе напорной магистрали. Для дождевальной установки - это атмосферное давление. Для системы топливопитания ГТД – это давление в камере сгорания: р_кс = π_дв·р_Н ; для системы смазки ГТД – это давление в среде, окружающей узел опоры: р = р_Н.

17. При расчете систем топливопитания и смазки давление перед форсунками получается неодинаковым в результате различных гидравлических потерь и разного расположения элементов. Для нормальной работы двигателя оно должно быть одинаковым. Поэтому рассчитываются перепады давлений между общим для всех форсунок сечением системы и сечением перед каждой форсункой. Общим сечением удобно считать сечение перед первым приточным тройником топливной системы и тройником симметричной формы с резким поворотом на 90˚ для дождевальной системы или системы смазки. При расчете используется, как и для всасывающей магистрали, уравнение Бернулли. В дополнение к предыдущим формулам приведем формулу для определения давления перед разветвлением потока:

р_i = р_i+1+ ρg(z_i+1-z_i) + - +∑ р_r ,

где

и_i+1 – скорость жидкости после бокового ответвления (правого или левого) тройника;

∑Δр_r – суммарные потери давления от общего сечения до расчетного. За расчетное сечение выбирается сечение перед отверстием форсунки, наиболее удаленной от общего сечения - базовой форсунки. Перед отверстием базовой форсунки давление равно

р = р_кс+ р_ф

для топливной системы, а для систем дождевания и смазки

р = р_Н+ р_ф.

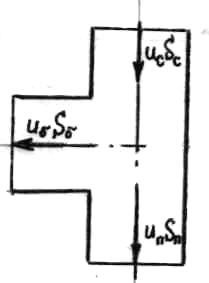
При определении суммарных потерь давления от общего сечения до расчетного в системах топливопитания и смазки необходимо в приточных тройниках 22, 25 и 26 соответственно вычислить потери полного давления на проход. Например, для тройника 22 топливной системы (рис.4.10) потери давления на проход, вычисленные по скорости жидкости в сборном рукаве равны:

. Для каждого тройника скорость в сборном рукаве имеет свое значение, так как происходит отбор расхода в боковое ответвление. Давление в выходном сечении тройника на проходе также определяется с помощью уравнения Бернулли, записанного для сечения входа в тро-

Рис.4.10

йник 1-1 и сечения выхода из тройника на проходе 2-2:

.

Граничные условия для тройника в рассматриваемом случае будут такие:

z₁=z_c= z₂=z_п, так как тройник - местное сопротивление. а потому его длина равна нулю;

р₁=р_с; u₁=u_c=Q_c/S_c; p₂=p_п=? - подлежит определению; u₂=u_п=Q_п/S_п; Q_п=Q_c - Q_ф.

После подстановки граничных условий в уравнение, находим выражение для давления на выходе на проходе:

.

Полученная формула показывает, что давление после прохода тройника может быть больше давления на входе в тройник.

Давление на выходе из тройника на боковом ответвлении находится аналогичным образом - применением уравнения Бернулли для сечения входа в тройник и сечения выхода из тройника в боком ответвлении.

18. После нахождения давления в общем сечении для всех форсунок участка нагнетания (в сборных рукавах тройника 8 дождевальной установки, тройника 22 топливной системы, тройника 20 системы смазки) вычисляем давление, которое дожжен создать основной насос. Для этого опять записываем и решаем уравнение Бернулли для участка нагнетания между выходным сечением основного насоса и сечением, общим для всех форсунок рассчитываемой гидросистемы.

19. При найденном значении давления на выходе из насоса необходимо вычислить давления перед каждой «небазовой» форсункой, чтобы убедиться в том, что перед базовой форсункой давление имеет наименьшее значение. Если окажется, что давление перед какой-либо форсункой меньше давления перед форсункой, принятой за базовую, то необходимо давление на выходе из насоса скорректировать, увеличив его на величину этой разности и на эту же величину повысить давление во всех характерных сечениях участка нагнетания, начиная с сечения, общего для всех форсунок.

20. На этом пункте расчета участка нагнетания производится расчет давлений в характерных сечениях. Расчет давлений производится по тому же алгоритму, который был использован при расчете давлений на участке всасывания

21. Вычисляется перепад давления на насосе р_н = р_нвых – р_нвх и его полезная мощность N=Δp_н·Q. Здесь Q=G/ρ - объемный расход жидкости, подаваемой насосом в участок нагнетания.

Параметры жидкости на участке всасывания Таблица 4

№ по схеме	Элемент	ρgz1	ρgz2	ρg(z1-z2)	р1	рr			-	p2
1	2	3	4	5	6	7	8	9	10	11
		кПа
1	бак	ρgz1	ρgz1	0	рб	0	0	0	0	рб
2	вход в тру- провод	ρgz1= ρg(l4+l6)	ρgz1	0	рб	Δрвх	0		-	p2=рб- - Δрвх
3	насос подкачки	ρgz1	ρgz1	0	p2				0	p3вых
4	трубопровод	ρg(l4+l6)	ρgl6	ρgl4	p3вых	Δрl4			0	p4вых=р3вых+ ρgl4- Δрl4
5	запорный кран

22. Определяются перепады давлений на дополнительных гидравлических сопротивлениях (жиклерах) которые должны обеспечить одинаковость давлений перед отверстиями форсунок, не являющихся базовыми.

23. Результаты расчета сводят в таблицы отдельно для всасывающего и напорного участков. Рекомендуется индекс 1 присваивать входу в рассматриваемый элемент, а индекс 2 - выходу из него. Например, для магистрали всасывания топливной системы (табл.4): в столбце 6 записываются значения давления на входе в элемент гидросистнмы, в столбце 7 - потери давления в элементе, в столбце 10 - разность динамических давлений на элементе, и в последний 11 столбец записываются значения давления на выходе рассматриваемого элемента гидросистемы. Таблица составлена таким образом, что, зная уравнение Бернулли, в соответствии с исходными данными можно вычислить давление на выходе из рассматриваемого элемента участка. Так, для примера, заполнены в буквенном виде первые 4 строки таблицы 4.

Таблица расчетных данных для участка нагнетания имеет особенности, связанные с наличием тройников. Тройники имеют один вход и два выхода - на проход и на боковое ответвление. Поэтому в таблице для участка нагнетания в строке для тройников необходимо приводить два значения параметров жидкости (динамического давления, потерь давления на проход и на боковое ответвление, статического давления) на выходе из тройника, используя соответствующие индексы (_п и _б): на проходе и на ответвлении.

24. На основании табличных данных строят графики (пример на рис.4.11): изменение величин р, , ρgz вдоль всасывающего и напорного участков (пример приведен для магистрали нагнетания топливной системы ВРД). Вертикальные участки линии давления отвечают изменению давления на местных сопротивлениях, наклонные – изменению давления вдоль трубопровода).

l₁₅ l₁₇ l₁₉ l₂₁ l₂₄ l₂₇

Рис.4.11

График рекомендуется строить следующим образом. Ось абсцисс делится на равных отрезков. Концам отрезков присваиваются номера характерных сечений - номера местных сопротивлений. Переменную величину, откладываемую по оси ординат, имеет смысл откладывать от значения, близкого к минимальному, а не от нулевого. Представленный на рис.4.11 график изменения давления воспринимается следующим образом. Давление, создаваемое основным насосом 14, уменьшается вдоль трубопровода l₁₅ на пути к отводу 16 не только за счет гидравлических потерь (путевых), но и за счет увеличения потенциальной энергии положения (увеличения z) - трубопровод l₁₅ расположен вертикально. В отводе 16 давление скачком уменьшается за счет местных потерь. Вдоль трубопровода l₁₇, расположенного горизонтально, давление в жидкости уменьшается только за счет путевых потерь. В фильтре 18 и подсоединенному к нему колену 28 давление изменяется скачкообразно. В трубопроводе 19 давление в жидкости при движении к тройнику 20 с одной стороны, в соответствии с основным законом гидростатики, увеличивается (увеличивается глубина погружения), а с другой стороны - уменьшается из-за линейных гидравлических потерь. До тройника 20 жидкость движется с постоянным динамическим давлением, как показывает его график. В тройнике 20 коллектора поток жидкости разветвляется на две половины. Разветвление потока происходит с потерями давления и уменьшением динамического давления в 4 раза. Так как топливный коллектор симметричен, то график строится только для одной половины коллектора - правой. При движении по коллектору к форсункам энергия положения жидкости не изменяется (это видно из графика ρgz), но давление уменьшается из-за путевых потерь в трубопроводе l₂₁. Разветвление потока в тройнике 22 сопровождается изменением статического и динамического давлений: уменьшение давления на проходе меньше, чем при развороте потока в боковое ответвление. В тройнике 25 изменение давления на проходе отличается от изменения давления в тройнике 22: давление в транзитном потоке (на проходе) увеличивается. При движении жидкости к форсунке 29 (конечной) давление в жидкости уменьшается как за счет путевых потерь в трубопроводе l₂₇ (линейно), так и за счет местных потерь в колене 28 (скачкообразно). Давление перед каждой форсункой коллектора показано на рассматриваемом графике как давление в боковом ответвлении тройников 22 и 26, а также давления на выходе из оконечного колена 28.