77

Курсовая работа

по гидравлике

Министерство образования и науки Российской Федерации

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ

УНИВЕРСИТЕТ им. А.Н.ТУПОЛЕВА

СЫЧЕНКОВ В.А., ЧЕФАНОВ В.М.

РАСЧЕТ ГИДРАВЛИЧЕСКИХ СИСТЕМ

Пособие к курсовой работе

по гидравлике для студентов заочной и очной

форм обучения

Казань 2011

УДК 532 (077)

Сыченков В.А., Чефанов В.М. Расчет гидравлических систем: Пособие к курсовой работе по гидравлике для студентов заочной и очной форм обучения/ Казань: Изд-во Казан. гос. техн. ун-та. 2011. 52с.

ISBN 5-7579-0325-2

Вследствие того, что пособие предназначено и для студентов заочной формы обучения, оно имеет несколько больший объем теоретического материала, позволяющий без предварительного прослушивания теоретического курса выполнить курсовую, контрольную или расчетно-графическую работы. Пособие содержит рекомендации к расчету гидросистем подачи жидкости. Представлены справочные материалы, необходимые для выполнения работы, приведены требования к оформлению работы.

Табл.18. Ил.46. Библиогр.:12 назв.

Рецензенты:

Заведующий кафедрой

«Газотурбинные энергоустановки и двигатели»

Казанского государственного энергетического университета

к.т.н. профессор Титов А.В.

Главный технолог КФ КБ ОАО «Туполев» к.т.н. Найшулер Б.И.

Рекомендовано к изданию Учебно-методическим центром

КГТУ им. А.Н.Туполева

ISBN 5-7579-0325-2 © Изд-во Казан. гос. техн. ун-та, 2011

© Сыченков В.А., Чефанов В.М., 2011

Посвящается

Владимиру Брониславовичу Панфиловичу,

автору прототипа работы

Введение

Курсовая работа должна способствовать приобретению знаний и навыков решения задач по разделу механики жидкости и газа – гидравлике. Для гидравлики типичен упрощенный одномерный подход к рассмотрению явлений движения жидкости. Сложный многомерный характер движения жидкости в одномерном рассмотрении учитывается эмпирическими коэффициентами или теоретическими величинами, позволяющими изучать неодномерное движение в одномерной постановке. Спецификой гидравлики является также широкое применение упрощенных и эмпирических методов решения задач с целью получения результатов и методик, удобных, для использования в инженерной практике.

В гидравлике изучают движение капельных жидкостей, то есть таких жидкостей, которые в малых количествах под действием поверхностного натяжения принимают сферическую форму, а в больших – образуют свободную поверхность раздела с газом. Важным свойством капельных жидкостей является то, что они ничтожно мало изменяют свой объем при изменении давления. Поэтому их считают несжимаемыми.

Широкое использование методов гидравлики во многих отраслях техники обусловлено тем, что большинство решений задач, полученных теоретической гидромеханикой, не может быть использовано в инженерной практике. В настоящее время в связи с широким применением численных методов и ЭВМ современная гидравлика представляет механику жидкости, опирающуюся на теоретический фундамент классической гидромеханики. В то же время гидравлика является прикладной наукой, в которой решение доводится до вида, удобного для инженерного применения.

1. Теоретические основы расчета гидравлических систем.

Несмотря на упрощенный подход к решению задач гидравлики, методика их решения основана на тех же основных законах и уравнениях, которые используются в механике жидкости и газа. Это законы сохранения массы, количества движения и энергии, которые в механике жидкости и газа записываются в виде уравнений неразрывности, движения и энергии. Так как гидравлика рассматривает одномерное движение несжимаемой жидкости, то уравнения движения и энергии становятся зависимыми, и для решения обычно достаточно использовать только два основных уравнений: уравнение неразрывности и уравнение энергии. Все уравнения и зависимости записываются для контрольного объема, представляющего неподвижный в пространстве объем, через который протекает жидкость. Поскольку гидравлическая система представляет в общем случае канал с твердыми стенками, направляющими движение жидкости, в качестве контрольного объема выступает либо вся система в целом, либо ее участок, ограниченный входным 1-1 и выходным 2-2 сечениями (рис.1.1).

Рис.1.1

Уравнение неразрывности в гидравлике называют уравнением расхода. Для участка системы, ограниченного сечениями 1-1 и 2-2 (рис.1.1), оно может быть записано в виде:

ρ₁u₁S₁ = ρ₂u₂S₂ (1.1)

или

G = ρuS = const, (1.1а)

где ρ – плотность жидкости (кг/м³), представляющая массу жидкости, заключенную в единице объема; и - среднерасходная скорость жидкости в сечении (м/с); S - площадь поперечного сечения канала (м²); G - массовый расход жидкости (масса жидкости, протекающая через поперечное сечение канала в единицу времени) (кг/с).

Сформулировать уравнение расхода для установившегося (неизменного во времени) течения можно следующим образом: масса жидкости, протекающая в единицу времени через любое поперечное сечение выделенного участка, постоянна.

Для несжимаемой жидкости плотность постоянна в любой точке потока, ввиду чего уравнение неразрывности (расхода) может быть записано:

u₁S₁ = u₂S₂ (1.2)

или

Q = uS = const, (1.2a)

то есть объем жидкости, протекающий через любое сечение выделенного участка системы в единицу времени, постоянен. Величина Q (м³/с), называется объемным расходом.

Приведенная запись уравнения расхода пригодна для участка, по длине которого нет подвода или отвода жидкости.

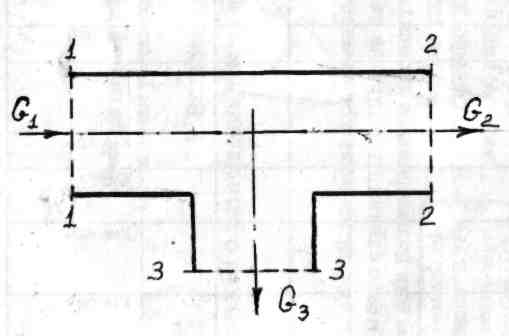
Рис.1.2

Для разветвленного участка, изображенного на рис.1.2, уравнение расхода имеет вид:

G₁ = G₂ + G₃

или

Q₁ = Q₂ + Q₃

Уравнение энергии в гидравлике записывают в форме, которая называется уравнением Бернулли. Применительно к рис.1 это уравнение записывается следующим образом:

ρgz₁ + р₁ + α₁ = ρgz₂ + р₂ + α₂ + р_r (Па). (1.3)

В этом уравнении

ρgz - энергия положения единицы объема жидкости в сечении, находящемся на высоте z от плоскости сравнения 0-0 (Па);

р - энергия давления единицы объема жидкости в сечении (Па);

u - среднерасходная скорость в сечении, вычисляемая по формуле ;

α - кинетическая энергия единицы объема жидкости в сечении (Па);

α - коэффициент Кориолиса, учитывающий неравномерность распределения ки-нетической энергии по сечению;

g = 9,81 м/с² - ускорение свободного падения;

р_r - потери энергии единицы объема жидкости в участке системы, выделенном сечениями 1 - 1 и 2-2 (Па).

Уравнение Бернулли можно представить в таком виде:

ρg ( z₁ – z₂) + (p₁ – p₂) = (α₂ u₂² - α₁ u₁² ) + р_r (Па).

В этом случае уравнение можно прочитать так: работа внешних сил, приложенных к жидкости на выделенном участке (работа сил тяжести - ρg(z₁ – z₂), работа сил давления -(p₁ – p₂), затрачивается на изменение кинетической энергии (α₂ - α₁ ) и работу против сил трения - р_r на выделенном участке. Определяя полное давление (давление торможения) как р^* = р+ρu²/2 , величину р_r называют потерями полного давления на длине выделенного участка системы.

Различают два вида потерь полного давления на гидравлическом сопротивлении.

Местные потери. Они проявляются в местах изменения формы, размеров или изменения направления движения, по отдельности или вместе. Вычисляются местные потери полного давления по формуле Вейсбаха;

р_м = ζ , (1.4)

где

ζ - коэффициент местного сопротивления, значение которого обычно определяется по справочным данным, в которых указывается сечение, определяющее потери;

u - среднерасходная скорость в определяющем сечении.

Рассмотрим основные виды местных гидравлических сопротивлений.

Потери при внезапном расширении трубы

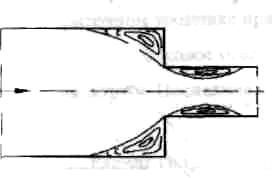
Потери при внезапном расширении канала называют потерями на «удар» Борда-Карно. Внезапное расширение трубы (канала) и схема течения показаны на рис.1.3.

Рис.1.3

Поток, выходя из трубы малого диаметра, расширяется не внезапно, как расширяется канал, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы большого диаметра образуется зона обратного течения с вихрями, которые и являются причиной потерь энергии в данном случае. При этом, как показывают наблюдения, происходит непрерывный обмен ча-

стицами жидкости между основным потоком и завихренной его частью.

Возьмем два сечения потока: 1 - 1 — в плоскости расширения трубы и 2 - 2-—в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то, следовательно, скорость его уменьшается, а давление возрастает. Поэтому второй пьезометр показывает высоту, на ΔH большую, чем первый; но, если бы потерь энергии в данном месте не было, то второй пьезометр показал бы еще большую высоту. Та высота h, которую мы здесь как бы недополучаем, и есть местная потеря напора на расширение.

Для потока жидкости в выбранных сечениях запишем уравнения неразрывности, Бернулли и движения. Полученную систему уравнений разрешим относительно местных потерь, полагая, что в сечении 1 -1 давление р₁ действует по всей площади S₂ и пренебрегая потерями на трение. Результатом решения является формула Борда-Карно для потерь напора при внезапном расширении

,

а после применения уравнения неразрывности

Следовательно, для случая внезапного расширения канала коэффициент сопротивления равен:

Когда площадь S₂ значительно больше площади S₁ и, следовательно, скорость u₂ можно считать равной нулю, потеря напора на расширение будет равна

,

т.е. теряется весь скоростной напор, а коэффициент потерь в этом случае ζ=1. Такому случаю соответствует подвод жидкости по трубе к баку большой емкости.

Постепенное расширение трубы

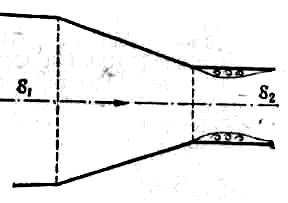
Рис.1.4.

Постепенно расширяющаяся труба назы-вается диффузором. Течение жидкости в диффу-зоре сопровождается уменьшением скорости и увеличением давления. Частицы движущейся жи-дкости преодолевают нарастающее давление за счет своей кинетической энергии, но последняя

уменьшается вдоль диффузора из-за увеличения площади канала, а также в направлении от оси к стенке из-за трения о стенки канала. Слои жидкости, прилежащие к стенкам, обладают столь малой кинетической энергией, что подчас они оказываются не в состоянии преодолевать повышенное давление, они останавливаются или даже начинают двигаться обратно. Основной поток наталкивается на эти противотоки, возникают вихреобразования и отрыв потока от стенки (рис.1.4). Интенсивность этих явлений возрастает с увеличением угла расширения диффузора, а вместе с этим растут и потери на вихреобразования в диффузоре.

Кроме того, в диффузоре имеются обычные потери на трение, подобные тем, которые возникают в трубах постоянного сечения.

Коэффициент сопротивления диффузора при расширении без учета трения /1/

,

где k зависит от угла конусности и может быть для α=5 - 20˚определен по приближенной формуле

k=sinα.

С учетом сопротивления трения коэффициент сопротивления диффузора вычисляется по формуле/1/:

,

где n=S₂/S₁ - степень расширения диффузора, λ - коэффициент путевых потерь (см. ниже).

Зависимость ζ=f(α), указана на рис.1.5. При угле α = 70° коэффициент потерь максимума, причем при угле α > 40 - 60° потери напора превосходят

α Рис.1.5.

потери при внезапном расширении потока (α= 180°). Поэтому вместо переходов в виде диффузоров с углом α > 40° нужно применять внезапное расширение как переход, дающий меньшие потери напора. При λ=0,015 - 0,025 и n=2 - 4 значе-ние угла раствора диффузора, при кото-

ром потери напора в нем будут минимальны, равно α_опт = 6. На практике для сокращения длины диффузора при заданном n обычно берут несколько большие углы, а именно, α = 7 - 9˚.Эти же значения угла α рекомендуется и для труб квадратного сечения. Для прямоугольных диффузоров (плоских диффузоров) оптимальный угол раствора больше, чем для круглых и квадратных, и составляет 10 –12^о.

Потери при сужении канала

Рис.1.6.

Рис.1.7.

Внезапное сужение (рис.1.6) вызывает меньшую потерю энергии, нежели внезапное расширение с таким же соотношением площадей. Основную долю потерь составляют

потери на вихреобразование при входе в трубу меньшего диаметра. Площадь поперечного сечения потока из-за образования области возвратного течения уменьшается. В расширяющейся части потока в малой трубе течение аналогично течению при внезапном расширении. Коэффициент потерь при внезапном сужении вычисляется по эмпирической формуле, предложенной И.Е.Идельчиком:

.

Из формулы следует, что в том частном случае, когда можно считать S₂/S₁ = 0, т. е. при входе в трубу из резервуара достаточно больших размеров и при отсутствии закругления входного угла, коэффициент сопротивления равен

ζ = ζ_вх = 0,5.

Закруглением входной кромки можно значительно снизить потери напора на входе в трубу.

Постепенное сужение трубы, т. е. коническая сходящаяся труба, называется конфузором (рис.1.7). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления; жидкость движется от большего давления к меньшему, поэтому причин к возникновению вихреобразований и отрыва потока (как это имеется в диффузоре) здесь нет. В конфузоре имеются лишь потери на трение. В связи с этим сопротивление конфузора всегда меньше, чем сопротивление такого же диффузора.

С учетом потерь на трение потери напора в конфузоре можно подсчитать по следующей формуле:

,

где п=S₁/S₂ —степень сужения конфузора.

Небольшие вихреобразования и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической частью. Для ликвидации этих вихреобра-

Рис.1.8.

зований и связанных с ними потерь рекомендуется коническую часть плавно сопрягать с цилиндрической или коническую часть заменять криволинейной, плавно переходящей в цилиндрическую (рис.1.8). При этом можно иметь весьма зна-чительную степень сужения при небольшой длине вдоль оси

и при весьма небольших потерях. Коэффициент сопротивления такого плавного сужения, называемого соплом, меняется примерно в пределах ζ = 0,03 - 0,10, в зависимости от степени сужения, плавности и числа Re (большим числам Re соответствуют малые значения ζ и наоборот),

Потери в поворотах

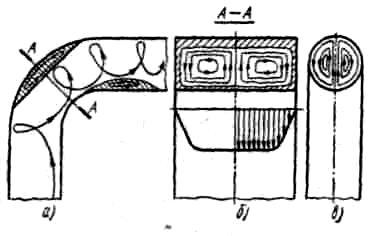
Рис.1.9. а - продольный разрез; б - поперечное сечение прямоугольного канала; в - поперечное сечение канала круглого сечения

Рис.1.10. Изменение профилей скоростей и давлений в колене и в трубе за ним

Плавный поворот трубы называется отводом. Схема течения представлена на рис.1.9. Появление радиального градиента давления в повороте приводит к возникновению так называемого парного вихря (см. поперечные сечения каналов), который, налагаясь на основной поток, придает линиям тока винтообразный характер. Кроме парного вихря, радиальный градиент давления в повороте служит причиной появления возвратных течений, как на внешней стороне поворота, так и на внутренней. Потери вызваны трением и вихреобразованием, в которой коэффициент потерь зависит от относительного радиуса R/d (R -средний радиус поворота, d - диаметр трубы) угла поворота δ и формы поперечного сечения канала и рассчитываются по формуле, предложенной Г.Н.Абрамовичем

,

где коэффициенты А, В и С учитывают влияние угла изогнутости отвода, относительного радиуса закругления отвода и относительной вытянутости поперечного сечения отвода Значения этих коэффициентов находятся в справочниках, например, в /5/.

Внезапный поворот трубы, или колено, вызывает значительные потери энергии, так как в нем происходят отрыв потока с вихреобразованиями (рис.1.10). Потери энергии тем больше, чем больше угол δ. Коэффициент потерь колена круглого сечения при δ=90˚ достигает значения 1,0. Поэтому применение колен не рекомендуется.

Потери при слиянии и разделении потоков.

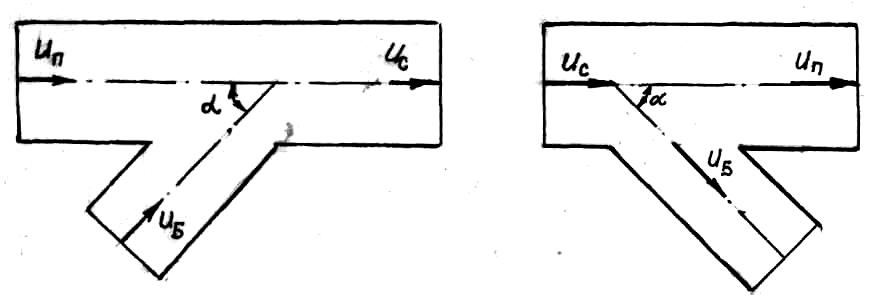
Слияние и разделение потоков происходит в тройниках (рис.1.11). Тройники разделяются на вытяжные и приточные. В вытяжном тройнике происходит слияние потоков (рис.1.11,а), а в приточном - разделение потоков (рис.1.11,б). Геометрически тройники характеризуются углом ответвления α и

а) б) Рис.1.11

отношениями площадей сечений обоих ответвлений SБ/SC, SП/SС и SБ/SП. В каждом тройнике могут изменяться отношения расходов QБ/QC и QП/QС. В гидросистеме с тройниками необходимо учитывать потери энергии и на боковое ответ-

вление и на проход, в зависимости от рассматриваемой ветви системы, при этом необходимо понимать, что в месте слияния или разветвления потоков давления одинаковы как в транзитном потоке, так и боковом. Для характеристики потерь в тройниках пользуются обычно коэффициентами местных потерь на боковое ответвление ζ_БС и коэффициентом местных потерь на проход ζ_ПС, вычисляемых в приведенном случае по скорости в сборном рукаве u_C. В вытяжном тройнике потери энергии обусловлены смешением потоков и потерями на поворот, иногда вызывающим местный отрыв потока.

В приточном тройнике при разделении потоков потери обусловлены потерями на поворот в боковое ответвление, а при проходе - потерями на внезапное расширение в месте разветвления потока. Последние резко растут при увеличении площади отвода, где потери вычисляются по скорости жидкости в сечении сборного рукава тройника.

Путевые потери. Это потери полного давления по длине трубы с прямой осью. Они вычисляются по формуле Дарси:

, (1.5)

где

λ - коэффициент путевых потерь (коэффициент Дарси);

l - длина трубы (м);

d - диаметр трубы (м).

Значение коэффициента путевых потерь λ зависят от режима течения жидкости на рассматриваемом участке системы. Различают ламинарный и турбулентный режимы течения. При ламинарном режиме частицы жидкости движутся по параллельным траекториям, без перемешивания, слоями. В турбулентном течении, наряду с главным, направленным движением, частицы жидкости совершают беспорядочные, хаотичные перемещения в продольном и поперечных направлениях. Поэтому турбулентное течение почти всегда сопровождается интенсивным перемешиванием жидкости и пульсациями скорости и давления.

Выявить режим течения жидкости в круглой трубе можно по значению числа Рейнольдса:

Re = = (1.6)

где ρ - плотность жидкости, (кг/м³); и - средняя скорость жидкости в трубе, (м/с); d - диаметр трубы, (м); μ - динамический коэффициент вязкости, (Па·с); v - кинематический коэффициент вязкости, (м²/с).

Значения ρ и μ определяются по справочным данным в зависимости от температуры и давления жидкости. В большинстве случаев зависимостью их от давления можно пренебречь. Могут применяться другие единицы измерения. Например, для динамического коэффициента вязкости используют: 1 кгс·с/м² = 9,81 Па·с или 1 П (пуаз) = 0,1 Па·с; для кинематического коэффициента вязкости: 1 Ст (стокс) = 100 сСт (сантистокс) = 10^-4 м²/с.

Ламинарный режим течения существует устойчиво при числах Рейнольдса Re ≤ 2300. При Rе > 2300 ламинарное течение теряет устойчивость. При Rе > 4000 течение является турбулентным. В диапазоне 2300 < Rе < 4000 течение является неустойчивым, такой режим течения называют переходным.

При ламинарном течении в круглой трубе распределение скорости по сечению трубы (профиль скорости) представляет параболу, а коэффициент Кориолиса α равен 2. При турбулентном течении профиль скорости близок к равномерному, поэтому α принимают равным 1.

При ламинарном течении коэффициент путевых потерь определяют по формуле Пуазейля:

(1.7)

Видно, что при ламинарном течении значение коэффициента путевых потерь не зависит от состояния омываемой жидкостью поверхности, не зависит от шероховатости стенки трубы.

Рис.1.12.

На переходном режиме течения Re =2000 ...4000 коэффициент путевых потерь определяется по графику на рис.1.12. Видно, что в указанном диапазоне коэффициент сопротивления быстро растет с увеличением Re.

При турбулентном течении на величину потерь влияет не только число Рейнольдса, но и шероховатость внутренней поверхности трубы. Среднюю высоту Δ бугорков шероховатости (рис.1.13а) называют абсолютной геометрической шероховатостью. Отношение средней высоты бугорков к диаметру трубы называют относительной шероховатостью. При турбулентном режиме течения в шероховатых трубах следует различать три режима. При умеренных числах Рейнольдса вблизи стенки трубы течение ламинарное, так как стенка подавляет пульсации скорости. Эта ламинарная пленка на стенке называется

	а)	ламинарным пограничным подслоем. Пока лами-нарный подслой покрывает бугорки шероховатости (рис.13,б), гидравлические потери обусловлены только внутренним трением в жидкости. Трубы при таком течении называются гидравлически гладкими, а коэффициент путевых потерь вычисляется по формуле Блазиуса:
	б)
Рис.1.13	в)	для 4000 < Re ≤ 105 (1.8) или по формуле П.К.Конакова:

λ = (1,8·lg Re - 1,64)^-2 для любых Re > 4000. (1.9)

Трубы с неравномерной шероховатостью (технические трубы) могут считаться гидравлически гладкими, если

.

С увеличением числа Рейнольдса ламинарная пленка становится тоньше, высокие бугорки шероховатости выступают из нее и увеличивают сопротивление движению жидкости (рис.1.13,в). Гидравлические потери в этом случае зависят от числа Рейнольдса и относительной шероховатости трубы. Дальнейшее увеличение числа Рейнольдса приводит к разрушению ламинарной пленки и потому величина гидравлических потерь перестает зависеть от числа Рейнольдса и определяется только относительной шероховатостью поверхности трубы. Таким образом, одна и та же труба в зависимости от режима течения жидкости может быть гидравлически гладкой или шероховатой. В большинстве технических задач можно полагать трубы гидравлически гладкими.

Третий режим, режим с полным проявлением шероховатости, часто называют еще автомодельным относительно числа Re или режимом квадратичной зависимости сопротивления от скорости. На этом режиме течения все элементы шероховатости выступают из ламинарного подслоя. Для вычисления коэффициента путевых потерь на этом режиме можно пользоваться формулой Шифринсона

(1.10)

Для всех турбулентных режимов А.Д. Альтшуль предложил приближенную формулу

. (1.11)

При малых значениях числа Рейнольдса (Re < 20/ ) формула (1.11) практически совпадает с формулой Блазиуса (1.8), а при Re→∞ с – формулой (1.10). Таким образом, путем сравнения численного значения отношения d/Δ с числом Рейнольдса можно установить границы режимов турбулентного течения в шероховатых трубах.

Если труба не круглая, то в качестве размера, определяющего число Рейнольдса, вместо диаметра используют величину d_Г = 4S/П, называемую гидравлическим диаметром. Здесь S - площадь поперечного сечения потока в трубе; П - смоченный периметр, то есть участок периметра сечения трубы, на котором жидкость соприкасается со стенками трубы. Нетрудно показать, что для круглой трубы d_Г = d; для полностью заполненной потоком жидкости трубы прямоугольного сечения d_Г = 2аb/(а+b), где а и b - стороны сечения; если труба прямоугольного сечения заполнена потоком жидкости на высоту с, то d_Г = 2аb/(а+2с); для кольцевого канала d_Г = 2∙δ, где δ - ширина кольца.

В строительстве и гидротехнике для расчета путевых (линейных) потерь давления (напора) используют иную формулу Дарси (1.5).

Записав формулу (1.5) для определения потерь напора по длине трубопровода l диаметром d (первую водопроводную формулу)

,

выразим из нее скорость, используя определение гидравлического радиуса R=d/4 и пьезометрического уклона i_p=h/l:

,

В полученной формуле называют коэффициентом Шези.

Объемный расход равен

.

Величину называют модулем расхода. Он равен расходу жидкости, при пьезометрическом уклоне, равном единице, i_p=1, и имеет размерность расхода.

Заменив в первой водопроводной формуле скорость через расход, получим вторую водопроводную формулу:

,

где величина K=l/q² называется удельным сопротивлением трубопровода; представляет собой потери напора при расходе, равном единице.