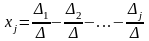- •5В070400 - «Есептеу техникасы және бағдарламалық қамтамасыз ету»
- •21. Матрицаның анықтауышын тап
- •84. Матрицаның анықтауышын тап
- •85. Матрицаның анықтауышын тап
- •86. Матрицаның анықтауышын тап
- •Вычислить косинус угла между векторами
- •Компланар емес - не компланарны
- •433. Матрицаның анықтауышын тап
- •437. Матрицаның анықтауышын тап
84. Матрицаның анықтауышын тап
Найти
определитель
матрицы К=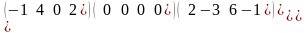
det K=0
det K=9
det K=3
det K= -21
det K= 21
85. Матрицаның анықтауышын тап
Найти
определитель матрицы К=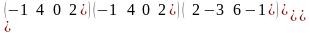
det K=0
det K=9
det K=3
det K= -21
det K= 21
86. Матрицаның анықтауышын тап
Найти
определитель матрицы К=
det K=0
det K=9
det K=3
det K= -21
det K= 21
87.Қандай шарт орындалса А-1 матрицасы А матрицасының (n-ші ретті квадратты) кері матрицасы деп аталады
Матрица А-1 называется обратной для матрицы А (квадратная порядка n), если выполняется условие
АА-1= А-1А= Е
А+А-1=Е
А-А-1=Е
АА-1=АТ
АТА-1=АТ=E
88. Берілгені: / Дано: К=М2х4В4х2
Матрицаның өлшемi неге тең
Чему равен размер матрицы
К2х2
К2х4
К4х2
К4х4
К4х1
89. Берілгені: / Дано: К=М3х4В4х2
Матрицаның өлшемi неге тең
Чему равен размер матрицы
К3х2
К2х3
К4х2
К4х4
К4х3
90. Берілгені: / Дано: К=М2х1В1х3
Матрицаның өлшемi неге тең
Чему равен размер матрицы
К2х3
К1х1
К1х3
К3х1
К3х2
91. Берілгені: / Дано: К=М5х4В4х1
Матрицаның өлшемi неге тең
Чему равен размер матрицы
К5х1
К5х4
К4х5
К1х5
К4х
92.
Берілгені: / Дано:
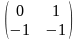
Матрицаның А12 алгебралық толықтауышын тап
Найти алгебраическое дополнение А12 матрицы
1
-1
0
2
-2
93. m қатардан n бағанадан тұратын mxn сандардын кесте түрiнде жазылуы
Совокупность mxn действительных чисел, расположенных в виде прямоугольной таблицы, где m – число строк, n – число столбцов таблицы называется
Тiк бұрышты матрица - Прямоугольной матрицей
Бiрлiк матрица - Единичной матрицей
Үшбүрышты матрица - Треугольной матрицей
Квадрат матрица - Квадратной матрицей
Нольдiк матрица - Нулевой матрицей
94. Берілгені: / Дано: А= ,
Транспонирленген матрицаны тап
Найти транспонированную матрицу
АТ=
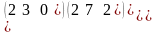
АТ=

АТ=

АТ=

Дұрыс жауабы жоқ - Нет правильного ответа
95. Егер матрицаның тiк жолы мен жатық жолы тең болса матрица қалай аталады
Если в матрице число строк равно числу ее столбцов, то такая матрица называется
Квадратты - Квадратной
Тiкбұрышты - Прямоугольной
Үшбұрышты - Треугольной
Бiрлiк - Единичной
Диогоналдық - Диагональной
96.
Егер теңдеулер жүйесiнiң b1 , b2 ,…,bm бiреуi нөлге тең болмаса қалай аталады
Если в системе уравнений хотя бы одно из чисел b1 , b2 ,…,bm не равно нулю, то система называется
Бiртексiз - Неоднородной
Бiртектi - Однородной
Үйлесiмсiз - Несовместной
Нөлдiк - Нулевой
Анықталған - Определенной
97.
Берілгені:
/
Дано: А=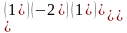 ,
В=
,
В= ,
,
Табу керек АВ
Найти АВ
АВ=
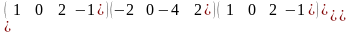
АВ=0
АВ=
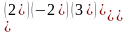
АВ=
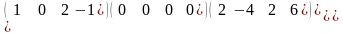
Дұрыс жауабы жоқ - Нет правильного ответа
98. Матрицасының анықтауышын есепте
Вычислить
определитель матрицы М=
–2
0
10
1
20
99. Матрицасының анықтауышын есепте
Вычислить
определитель матрицы М=
7
0
-2
-7
2
100. Матрицасының анықтауышын есепте
Вычислить
определитель матрицы М=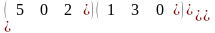
11
10
-11
-10
0
101. Крамер формуласын көрсет
Формулы Крамера имеют вид
102. Диогоналдан басқа элементтерiн нөлге айналдырып теңдеулер жүйесiн шешу әдiсi
Метод решения системы путем последовательного исключения переменных называется методом
Гаусс - Гаусса
Крамер - Крамера
Керi матрица - Обратной матрицы
Қосу - Сложения
Чебыш - Чебышева
103.
Берілгені:
/
Дано:
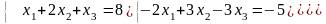
Теңдеу жүйесiн шеш
Решить систему уравнений
1;2;3
4;3;1
2;2;1
0;1;1
3;1;0
104.
Берілгені:
/
Дано:
 ,
,

Қай кезде векторлар параллель болады?
Когда векторы будут параллельны?
 ;
;
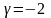
 ;
;

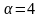 ;
;
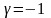
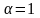 ;
;

 ;
;

105.
Берілгені:
/
Дано:
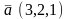 ,
,
 .
.
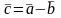 векторының
ұзындығын
тап
векторының
ұзындығын
тап
Найти длину вектора

1
13
3

106. Берілгені: / Дано: , .
 векторының
ұзындығын
тап
векторының
ұзындығын
тап
Найти длину вектора

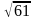
61
(5,3,0)
34
107. Берілгені: / Дано: , .
векторының координаттарын тап
Найти координаты вектора
(5,3,0)
(1,1,2)
(0,3,4)
34
108.
Берілгені:
/
Дано:
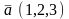 ,
,

векторының координаттарын тап
Найти координаты вектора
(1,3,0)
(1,1,6)
(1,-2,9)
(3,1,4)
(0,1,6)
109.
Берілгені:
/
Дано:
 ,
,

векторының координаттарын тап
Найти координаты вектора
(4,7,-2)
(-4,-9,8)
(-4,7,-2)
(4,9,-8)
(4,7,8)
110. Берілгені: / Дано: 3х+у+4=0 түзуге перпендикуляр болып, (-2,0) нүктесі арқылы өтетiн түзудiң теңдеуiн көрсет
Уравнение прямой, проходящей через точку (-2,0), перпендикулярно прямой 3х+у+4=0, имеет вид
у=х/3+2/3
у=х/3-2/3
у=х/3
у=-3х-6
у=-х/3-2/3
111.
Берілгені:
/
Дано:
 ,
,
 .
.
Векторлардың арасындағы бұрыштың косинусын тап
Найти косинус угла между векторами
16/25
1/25
4/25
8/25
16/5
112.
Берілгені:
/
Дано:
 ,
,
 .
.
векторының ұзындын тап
Найти длину вектора
3

1
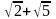
0
113.
Берілгені:
/
Дано:
 ,
.
,
.
векторпының координаттарын тап
Найти координаты вектора
(0,0,8)
(1,1,6)
(3,1,4)
(1,3,0)
(0,1,6)
114.
Берілгені:
/
Дано:
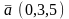 ,
,
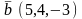 .
.
Векторлардың
 скаляр
көбейтiндiсi
тең
скаляр
көбейтiндiсi
тең
Скалярное произведение равно
-3
(0,7,2)
3
10
0
115. Берiлген түзулердiң қайсылары перпендикуляр
Из перечисленных прямых перпендикулярными являются
1) у=4х+1; 2) у=2х-3; 3) у=-х/2+4;
4) у=-4х-5
2,3
3,4
1,4
2,4
1,2
116.
Берілгені:
/
Дано:
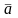 {1,-1,0}
{1,-1,0}
Векторлардың ұзындығы
Длина вектора равна

–1
2
0
-2
117. Берiлген түзулердiң қайсылары паралель
Из перечисленных уравнений прямых параллельными являются
1) 3х-4у+5=0; 2) 2х+5у-4=0;
3) 6х-8у-3=0; 4) у=3х/4+2; 5) 3х-5у+5=0
1,3,4
2,3,4
1,3,4,5
1,2,5,
2,4,5
118.
Берілгені:
/
Дано:
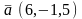 ,
,
 .
.
Скаляр көбейтiндiсi тең
Скалярное произведение равно
–19
(0,-4,-15)
19
10
0
119.
Берілгені:
/
Дано:
 ,
.
,
.
Векторлардың арасындағы бұрыштың косинусы тең
Косинус угла между ними равен
4/5
1/25
4/25
8/25
16/5
120.
Берілгені:
/
Дано:
 ,
,
 .
.
Берiлген векторлар перпендикуляр болады егер
Эти векторы будут перпендикулярны, если
121.
Берілгені:
/
Дано:
 ,
,
 .
.
Берiлген векторлар паралель болады,егер
Эти векторы будут параллельны, если
122.
Берілгені:
/
Дано:
 ,
.
,
.
векторының кординатасы тең
Координаты вектора равны
(5,1,0)
(0,-2,-9)
(5,3,-6)
(1,3,0)
(0,1,6)
123. (2,3) жґне (-1,0) нүктелерi арқылы өтетiн түзудiң теңдеуi
Уравнение прямой, проходящей через точки (2,3) и (-1,0) имеет вид
у=х+1
2у=3х-1
у=х/2+3
у=х-7
у=5х+1
124. Түзулердiң паралелдiк шарты қай түрде жазылады
Условие параллельности прямых записывается в виде
k1=k2
k1k2=-1
k1=-k2
k1k2=1
k1/k2=-1
125. Түзулердiң перпендикулярлық шарты қай түрде жазылады
Условие перпендикулярности прямых записывается в виде
k1k2=-1
k1=-k2
k1k2=1
k1/k2=-1
k1=k2
126.Бұрыштық коэффициент арқылы
берiлген және ордината осьiн қиятын теңдеу қайсы?
Каков вид уравнения прямой с данным угловым коэффициентом и отсекающей на оси ординат данный отрезок?
y=kx +b
y-y0=k(x-x0)
 =
=
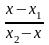
Ax+By+C=0
x cos +y sin -p =0
127.Бұрыштық коэффициент арқылы
берiлген және жазықтықта берiлген нүкте М(х0,у0) арөылы өтетiн түзудiң теңдеуi?
Каков вид уравнения прямой с данным угловым коэффициентом и проходящей через данную точку М(х0,у0) на плоскости?
y-y0=k(x-x0)
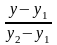 =
=
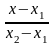
Ax+By+C=0
x cos +y sin -p =0
y=kx+b
128.Жазықтықта берiлген 2 нүкте арқылы өтетiн түзудiң теңдеуi.
Каков вид уравнения прямой, проходящей через две данные точки на плоскости?
=
Ax+By+C=0
x cos +y sin -p =0
y=kx+b
y-y0=k(x-x0)
129.Жазықтықтағы түзудiң жалпы теңдеуi қайсы?
Каков вид общего уравнения прямой на плоскости?
Ax+By+C=0
x cos +y sin -p =0
y=kx+b
y-y0=k(x-x0)
=
130.Жазықтықтағы түзудiң нормаль теңдеуi қайсы?
Каков вид нормального уравнения прямой на плоскости?
xcos +ysin - p =0
y=kx+b
y-y0=k(x-x0)
=
Ax+By+C=0
131.Кесiндiлiк түрде берiлген түзу теңдеуi.
Каков вид уравнения прямой в отрезках на осях на плоскости?

х=а
y =b
y=0
x=0
132.Ордината осьiне параллель болатын түзудiң теңдеуi.
Каков вид уравнения прямой, параллельной оси ординат на плоскости?
х=а
y =b
y=0
x=0
133.Абсцисса осьiне параллель болатын түзудiң теңдеуi.
Каков вид уравнения прямой, параллельной оси абсцисс на плоскости?
y =b
y=0
x=0
х=а
134.Абсцисса осьiнiң теңдеуi қайсы?
Каков вид уравнения оси абсцисс?
y =0
x=0
х=а
y =b
135.Ордината осьiнiң теңдеуi қайсы?
Каков вид уравнения оси ординат
x=0
х=а
y =b
y =0
136.
Берілгені:
/ Дано:
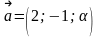 ,
,

векторлар
коллинеар болатындай
 мен
мен
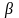 -ның
мәндерін табыңыздар.
-ның
мәндерін табыңыздар.
Определить, при каком значениях и векторы коллинеарны
А)
В)

С)
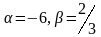
Д)

Е)

137.
Берілгені:
/
Дано:
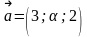 ,
,

векторлар коллинеар болатындай мен -ның мәндерін табыңыздар.
Определить, при каком значениях и векторы коллинеарны
А)

В)
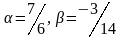
С)
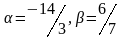
Д)

Е)

138.
Берілгені:
/ Дано:
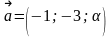 ,
,
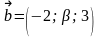
векторлар коллинеар болатындай мен -ның мәндерін табыңыздар.
Определить, при каком значениях и векторы коллинеарны.
А)
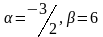
В)
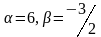
С)

Д)
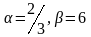
Е)
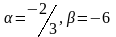
139.
Берілгені:
/ Дано:
,

векторлар коллинеар болатындай мен -ның мәндерін табыңыздар.
Определить, при каком значениях и векторы коллинеарны
.
А)

В)

С)
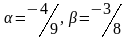
Д)

Е)

140.
Берілгені:
/ Дано:
 ,
,
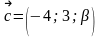
векторлар коллинеар болатындай мен -ның мәндерін табыңыздар.
Определить, при каком значениях и векторы коллинеарны.
А)

В)

С)
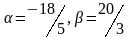
Д)

Е)

141.
Центрі
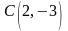 нүктесінде жататын, радиусы
нүктесінде жататын, радиусы
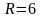 болатын шеңбердің теңдеуін жаз.
болатын шеңбердің теңдеуін жаз.
Составить уравнение окружности с центром в точке и с радиусом .
А)
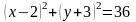
В)

С)

Д)

Е)

142. Центрі координаттың бас нүктесінде жататын, радиусы болатын шеңбердің теңдеуін жазыңыз.
Составить уравнение окружности с центром в начале координат и с радиусом .
А)
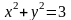
В)

С)
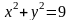
Д)

Е)

143.
Центрі
 нүктесінде жататын радиусы
нүктесінде жататын радиусы
 болатын шеңбердің теңдеуін жазыңыз.
болатын шеңбердің теңдеуін жазыңыз.
Составить уравнение окружности с центром в и с радиусом .
А)
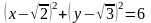
В)

С)
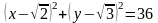
Д)

Е)

144.
Центрі
 нүктесінде жататын, радиусы
нүктесінде жататын, радиусы
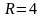 болатын шеңбердің теңдеуін жазыңыз.
болатын шеңбердің теңдеуін жазыңыз.
Составить уравнение окружности с центром в точке и с радиусом .
А)

В)

С)

Д)

Е)

145.
Центрі
 нүктесінде жататын радиусы
нүктесінде жататын радиусы
 болатын шеңбердің теңдеуін жазыңыз.
болатын шеңбердің теңдеуін жазыңыз.
Составить уравнение окружности с центром в точке и с радиусом .
А)
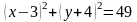
В)

С)
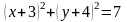
Д)
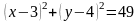
Е)
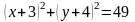
146.
Берілгені:
/
Дано:
 -
эллипс
-
эллипс
Табу керек оның жарты өстерін.
Найдите его полу оси.
А)
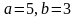
В)

С)
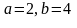
Д)

Е)
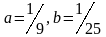
147.
Берілгені:
/ Дано:
 - эллипс.
- эллипс.
Табу керек оның жарты өстерін.
Найдите его полу оси.
А)

В)

С)

Д)
Е)
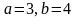
147.
Берілгені:
/ Дано:
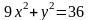 - эллипс.
- эллипс.
Табу керек оның жарты өстерін.
Найдите его полу оси
А)

В)

С)

Д)
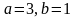
Е)
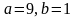
148.
Берілгені:
/ Дано:
 - эллипс.
- эллипс.
Табу керек оның жарты өстерін.
Найдите его полу оси.
А)
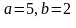
В)

С)

Д)

Е)

149.
Берілгені: / Дано:
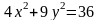 - эллипс.
- эллипс.
Табу керек оның жарты өстерін.
Найдите его полу оси.
А)
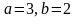
В)
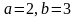
С)
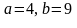
Д)

Е)
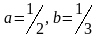
150.
Берілгені: / Дано:
 - гипербола.
- гипербола.
Табу керек оның жарты өстерін.
Найдите его полу оси.
А)
В)

С)

Д)
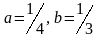
Е)
151.
Берілгені: / Дано:
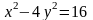 - гипербола.
- гипербола.
Табу керек оның жарты өстерін.
Дана гипербола . Найдите его полу оси.
А)
В)
С)
Д)
Е)

152.
Берілгені: / Дано:
 - гипербола.
- гипербола.
Оның жарты өстерін табыңыз.
Найдите его полу оси.
А)

В)
С)

Д)
Е)

153.
Берілгені: / Дано:
 - гипербола.
- гипербола.
Оның жарты өстерін табыңыз.
Найдите его полу оси.
А)
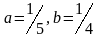
В)

С)

Д)
Е)

154.
Берілгені:
/
Дано:
 -
гипербола.
-
гипербола.
Оның жарты өстерін табыңыз.
Найдите его полу оси.
А)
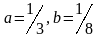
В)

С)

Д)

Е)

155. -нің қандай мәнінде қандай төмендегі екі жазықтықтың біріне-бірі перпендикуляр болады:
Определить,
при каком значении
следуюшие
пары уравнений будуть определить
перпендикулярные плоскости:

А) 6
В) 5
С) 4
Д) 3
Е) 1
156. -нің қандай мәнінде төмендегі екі жазықтықтың біріне-бірі перпендикуляр болады:
Определить, при каком значении следуюшие пары уравнений будуть определить перпендикулярные плоскости:

А) -19
В) -18
С) -15
Д) -16
Е) -13
157. -нің қандай мәнінде төмендегі екі жазықтықтың біріне-бірі перпендикуляр болады:
Определить, при каком значении следуюшие пары уравнений будуть определить перпендикулярные плоскости:
 ,
,
 .
.
А)

В)

С)

Д)
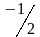
Е)

158. -нің қандай мәнінде төмендегі екі жазықтықтың біріне-бірі перпендикуляр болады:
Определить, при каком значении следуюшие пары уравнений будуть определить перпендикулярные плоскости:
 ,
,
 .
.
А) 5
В) 4
С) 3
Д) 2
Е) 1
159. -нің қандай мәнінде төмендегі екі жазықтықтың біріне-бірі перпендикуляр болады:
Определить, при каком значении следуюшие пары уравнений будуть определить перпендикулярные плоскости:
 ,
,
 .
.
А)
В)
С)

Д)

Е)
160. Координаталардың бас нүктесінен
 жазықтығына
дейінгі қашықтықты табыңыз.
жазықтығына
дейінгі қашықтықты табыңыз.
Вычислить расстояние от начала координат до .
А) 25
В) 24
С) 24
Д) 16
Е) 35
161.
 және
және
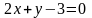 түзулерін арасындағы бұрышты табыңыз.
түзулерін арасындағы бұрышты табыңыз.
Вычислить
угол
 между
прямыми
и
.
между
прямыми
и
.
А)
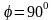
В)

С)

Д)
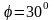
Е)
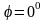
162.
Берілгені:
/ Дано:
 ,
,

-нің қандай мәнінде векторлар перпендикуляр болады.
При каком значении векторы перпендикулярны
А)

В)

С)
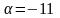
Д)


Е)

163.
Берілгені:
/
Дано:
 ,
,

векторлары арасындағы бұрыш косинусын есептеңіз.