Лабораторна робота № 3 «Теорія двоїстості. Стійкість оптимального плану»
3.1. Мета роботи – ознайомлення з особливостями побудови математичної моделі пари спряжених задач на прикладі задачі про оптимальне використання ресурсів, визначення двоїстих оцінок та дослідження стійкості оптимального плану.
3.2. Змістовна постановка задачі та її математична модель
Повернемося
до задачі про оптимальне використання
ресурсів. Припустимо, що підприємство
може не тільки використовувати наявні
ресурси для виробництва продукції, але
і реалізовувати сировину, якщо останнє
є більш вигідним. Позначимо через
(
)
умовну,
або маргінальну
(тіньову)
ціну
одиниці сировини
-го
виду, запаси якої на підприємстві
дорівнюють
(
).
Умовна ціна залежить від прибутків, які
підприємство очікує отримати від
реалізації готової продукції, що
вироблена з цієї сировини: чим вище ці
прибутки, тим більшу ціну можна отримати
від реалізації ресурсів, якщо реалізовувати
сировину більш вигідно, ніж продукцію,
яка вироблена з цієї сировини.
Задача про визначення граничних значень умовних цін, при перевищенні яких виробництво стає менш вигідним, ніж реалізація сировини, є двоїстою до задачі про оптимальне використання ресурсів. Обидві задачі утворюють симетричну пару спряжених взаємно двоїстих задач, і математична модель двоїстої задачі може бути побудованою за математичною моделлю вихідної згідно з їх властивостями. У тому випадку, коли математична модель вихідної задачі задана у стандартній формі, математичні моделі спряжених задач є симетричними. Тоді у матричній формі співвідношення між математичними моделями вихідної та двоїстої задач має вигляд:
-
Вихідна задача
Двоїста задача
(3.1)
,
,
.
.
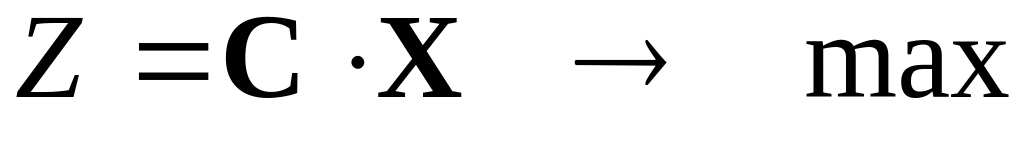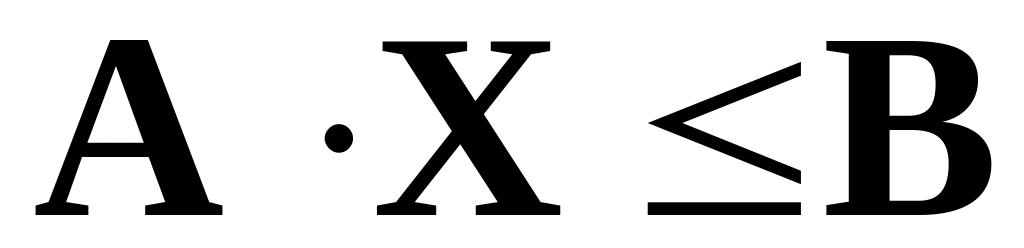Побудуємо модель двоїстої задачі за її економічним тлумаченням.
Оскільки покупець прагне придбати сировину якомога дешевше, критерієм ефективності двоїстої задачі буде загальна вартість усіх видів ресурсів, яка досліджується на мінімум. Тобто маємо цільову функцію:
. (3.2)
Зрозуміло,
що підприємство продаватиме наявні
ресурси лише за умов, що кошти, які воно
може отримає від реалізації сировини,
не будуть нижчі, ніж очікувані прибутки
від реалізації готової продукції. Цю
умову можна записати як рівність
екстремальних значень цільових функцій
спряжених задач:
,
що відповідає 1-й
теоремі двоїстості.
Як
і в задачі про оптимальне використання
сировини, матриця
–
це матриця технологічних коефіцієнтів,
а елементи
матриці-рядка
,
визначають прибуток підприємства від
реалізації одиниці продукції
-го
типу. Розглянувши умову беззбитковості
за кожним видом готової продукції,
отримаємо систему нерівностей:
(3.3)
Система нерівностей (3.3) є основною системою обмежень задачі, що є двоїстою до задачі про оптимальне використання сировини. Отже, коефіцієнтами при невідомих у цій системі є елементи транспонованої матриці технологічних коефіцієнтів, а її правою частиною – елементи транспонованої матриці прибутку від реалізації.
Оскільки ціни, навіть умовні, не можуть бути від’ємними, то для змінних двоїстої задачі маємо обмеження на знак:
. (3.4)
Отже, математична модель двоїстої задачі (3.2 – 3.4) відповідає співвідношенням (3.1), які випливають з теорем двоїстості.
Розв’язком
двоїстої задачі буде матриця-рядок
,
елементами якої є тіньові ціни. Вони
задовольняють системі обмежень (3.3) та
(3.4), і цільова функція
досягає мінімуму. Якщо ціни на сировину
перевищуватимуть тіньові ціни,
підприємству стає більш вигідним продати
сировину, ніж виробляти з неї продукцію.