4. Розрахунок за допустимими навантаженнями

Метод розрахунку за допустимим напруженням не дає змоги пов­ністю використати несівну здатність матеріалу конструкції. Це пов'язано з тим, що вичерпання несівної здатності пластичних мате­ріалів зумовлене досягненням ст_т, а крихких матеріалів — з досяг­ненням за . Втім можна задати умову, щоб дійсне на­вантаження на конструкцію не перевищувало деякого допустимого

де , тобто за допустиме навантаження вибирати лише частину граничного руйнівного.

Отже, граничне навантаження для стрижня із пластичного ма­теріалу знаходять за формулою

для крихкого – за формулою

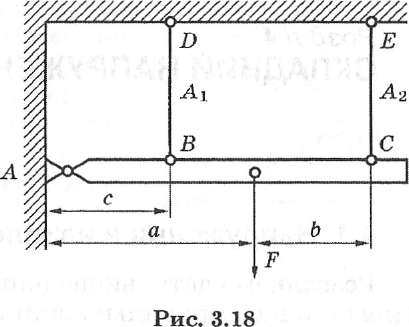
Знайдемо граничне наванта­ження для системи, яка показана на рис. 7.

Рис. 7

Брус передбачається абсо­лютно жорстким, а стрижні і виготовлені відповідно із м'якої сталі і крихкого матеріалу з площинами поперечного перерізу , . Із рівняння статики знахо­димо

Звідки

Умова міцності

Контрольні запитання

1. Як визначити напруження у перпендикулярному до осі розтягу перерізі?

2. Визначте абсолютну і відносну деформації призматичного стрижня.

3. Сформу­люйте закон Гука.

4. Вкажіть фізичний зміст модуля Юнга, його розмірність та середнє значення для деяких матеріалів.

5. Напишіть коефіцієнт Пуассона та вкажіть його середнє значення для металів.

6. Нарисуйте діаграму розтягу і назвіть основні її характеристики.

7. Яка різниця в характері руйнування за стиску крихких і пластич­них матеріалів?

8. Дайте визначення допустимого напруження. Від чого залежить величина коефіцієнта міцності?

9. Дайте визначення сталого опору.

10. Які задачі є статично невизначними? Назвіть методи їх визначення.

11. Як розраховують міц­ність сферичної або циліндричної оболонки?

Приклад.

Дано: , , , , .

Визначити: Напруження в перерізах колони

Розв'язок

1. Статична сторона задачі:

(1)

2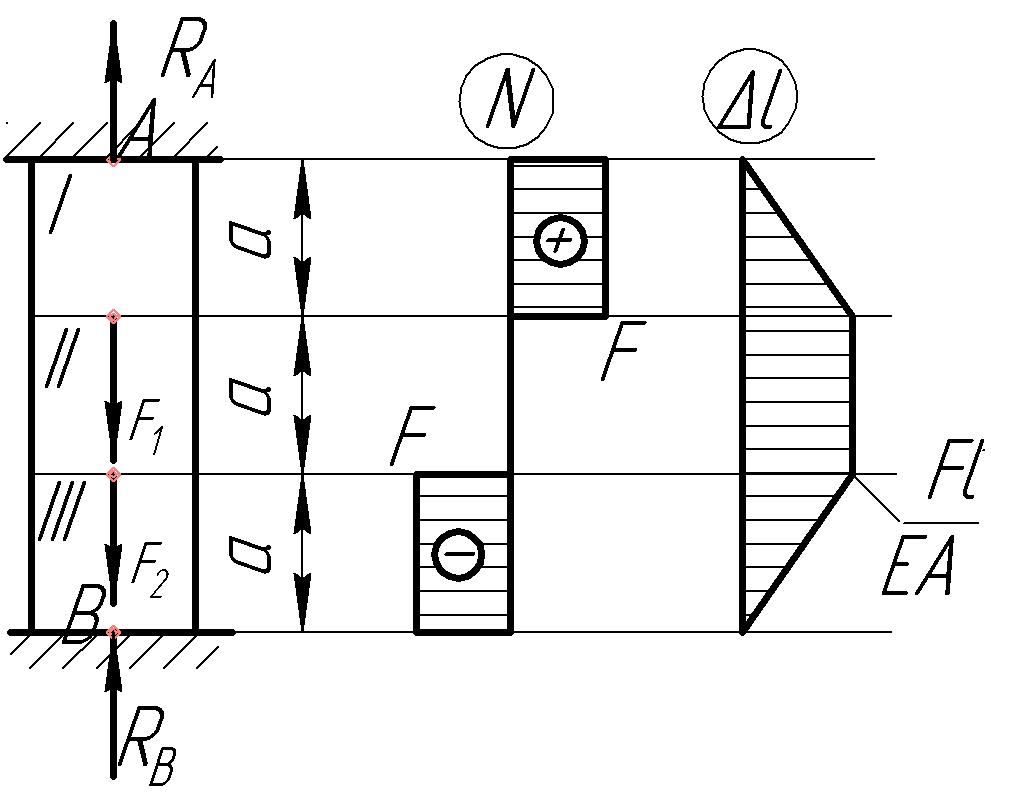 . Геометрична сторона задачі:

. (2)

3. Фізична сторона задачі:

. (3)

4. Синтез.

Так як і , а то:

.

Підставивши це значення в (1) будемо мати; що ; Таким чином:

; ;

58