Лекція №4 Статично невизначні конструкції

План лекції:

1. Статично невизначні стержневі системи.

2. Розрахунок гнучких ниток

3. Розрахунок тонкостінних посудин (оболонок)

4. Розрахунок за допустимими навантаженнями

Література : [1] – с. 130-140, с. 386-412; [2] – с. 72-91, с. 433-447.

1. Статично невизначні стержневі системи.

Н а практиці окрім статично визначних систем досить часто приходиться мати справу з конструкційними системами зусилля в яких визначити одними рівняннями статики неможливо. Такі системи називаються статично невизначними.

Прикладом таких систем може служити стержнева підвіска, кронштейн, опорна колонка і ін.

В статично невизначних системах (СНС) кількість невідомих зусиль, що визначається більша числа рівнянь рівноваги. І, чим ця різниця вища, тим більше статично невизначною буде система.

Статична невизначність системи позначається буквою , тобто буква показує скільки "зайвих" зв'язків накладено на дану конструкцію.

1.1 Існує декілька методик розв'язання статично невизначних задач. Так один з шляхів розв'язку пов'язаний з розглядом чотириєдиної задачі опору матеріалів:

1) Статична сторона – в якій складаються всі необхідні рівняння рівноваги.

2) Геометрична сторона – де оцінюються деформації системи. Рівняння, що описують деформацію, називаються рівняннями сумісності деформацій, їх кількість завжди дорівнює ступеню статичної невизначності системи.

3) Фізична сторона – в якій встановлюється зв'язок між деформаціями і зовнішніми зусиллями чи деформаціями і напруженнями.

4) Синтез – тобто сумісний розв'язок трьох попередніх залежностей.

П p и к л а д 1. Знайти реакції бруса (R_A, R_B) сталого перерізу (рис. 2) із закріпленими жорстко кінцями і навантаженого в перерізі m - n силою F. Із рівняння статики одержимо одне рівняння з двома невідомими:

Рис. 3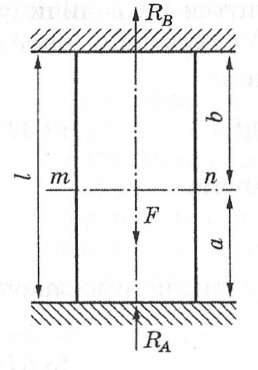

Геометричний бік задачі виражає умову сумісності деформації бруса — видовження всього стрижня дорівнює нулю, оскільки кінці стрижня жорстко закріплені: Рис. 2

;

Отже, скорочення нижньої частини під дією реакції R_A дорівнює видовженню верхньої частини під дією реакції R_B:

Розв'язавши рівняння, одержимо

;

П p и к л а д 2. Вплив температури. B деталях машин і елементах конструкції виникають напруження не тільки від дії зовнішніх навантажень, а й зі зміною температури всієї системи або двох окремих частин.

Досить значні температурні напруження відбуваються під час зварювання металевих елементів конструкції в одну безперервну лінію. Зі зміною температури в цих елементах діють напруження розтягу або стиску. Цю задачу схематизують як стрижень, закріплений нерухомо за температури (рис. 3). Знайти напруження, які виникають за зміни температури від до . Довжина стрижня , площа поперечного перерізу А, модуль пружності E. У разі підвищення температури від до стрижень намагається видовжитись і тисне на опори A і В, з боку яких діятимуть реакції.

Задача є статично невизначною, тому використаємо додаткову умову, що довжина стрижня залишається незмінною: температурне розширення дорівнює скороченню , яке спричинене дією навантажень.