Задача дт.6. Динаміка відносного руху точки

Диск обертається навколо осі, яка проходить через центр перпендикулярно його площині за законом (рад). Матеріальна точка М масою (кг) рухається вздовж радіуса диска за законом (м).

Записати рівняння відносного руху точки та визначити сили інерції, які діють на матеріальну точку на заданий момент часу t₁ (c). Вектори всіх сил інерції зобразити на рисунках у двох проекціях: вигляд згори і збоку. Дані приведені у таблиці.

Таблиця 6

Вихідні дані для задачі ДТ.6

№	m	a	b	c	d	e	f	t1	№	m	a	b	c	d	e	f	t1
1	4,4	1	-1	-2	-1	2	1	2	16	2	-1	2	-2	-1	3	1	2
2	3	-2	5	8	1	-1	-1	2	17	4,2	1	-3	1	-1	-2	5	2
3	3,1	1	-4	3	-1	2	3	2	18	2,9	1	-3	-5	1	-1	-4	2
4	3,6	-1	2	-4	2	1	-6	1	19	2,2	-1	2	6	1	-2	3	1
5	1,6	2	-1	-2	2	1	-5	1	20	1,9	1	-4	1	0	-2	5	2
6	3,5	1	-2	6	3	-3	-3	2	21	4,4	1	-3	-1	0	-2	1	2
7	4,5	0	1	-5	1	-3	-2	2	22	5,1	-1	4	-3	-1	2	3	2
8	1	-1	-2	6	-2	0	4	1	23	2,4	2	-6	-3	2	-5	1	2
9	3	1	0	-2	-2	4	-3	2	24	1,1	-1	5	-2	-1	3	2	3
10	2,4	-2	3	3	-3	1	4	1	25	2,5	-2	3	-2	-2	2	-3	1
11	1,5	1	-2	2	2	-2	-7	2	26	5,7	1	-2	1	-1	-1	2	2
12	2,6	-3	-2	1	2	-1	-2	1	27	3,3	1	-3	-4	-1	0	5	2
13	4,8	0	-2	1	-1	3	1	3	28	4,8	1	-5	-3	1	-4	2	3
14	2,5	1	-3	-3	1	-3	1	2	29	3,8	2	-5	1	-6	2	-3	1
15	5,1	1	-2	-4	-2	-1	1	1	30	5,5	-1	6	2	1	-5	3	4

Приклад. Диск обертається навколо осі, яка проходить крізь центр перпендикулярно його площині за законом (рад). Матеріальна точка М масою = 2 кг рухається вздовж радіуса диска за законом S = ОМ = (м). (O – центр диска, положення точки М на малюнку відносно центра визначає додатній напрям руху точки – дивись рис. 15).

Визначити сили інерції, які діють на матеріальну точку на момент часу t₁ = 2 c.

Розв’язок. В даному випадку сили інерції зумовлені як обертальним рухом системи (диска), так і відносним рухом точки по ньому. Таким чином, при визначенні сил інерції треба враховувати сили інерції, пов’язані з нерівномірним рухом диску та силу інерції Коріолиса:

,

.

Ц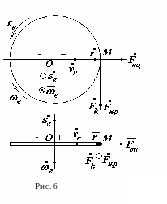 е значить, що для розв’язку задачі нам треба визначити положення матеріальної точки (тобто ), відносно осі обертання, її відносну швидкість , кутову швидкість диску та його кутове прискорення .

Знайдемо положення точки М на диску в даний момент часу, підставляючи цей час в рівняння відносного руху точки

S = ОМ = -2³ + 2·2² + 2 = 2 (м).

Таким чином, вектор відносного положення точки М лежить в площині диску, спрямований по радіусу у додатному напрямі та має модуль 2 м (рис. 6).

Знайдемо відносну швидкість точки М як першу похідну рівняння відносного руху за часом

v_r = = .

Для моменту часу t₁ = 2 с отримаємо v_r = - 3 (м/с). Від’ємне значення швидкості означає, що точка М рухається від точки до осі обертання.

Кутову швидкість обертального руху диску ω_е знайдемо як першу похідну кута повороту диска за часом

= ,

і, підставляючи t₁ = 2 с, отримуємо

= 6·2² – 2·8 – 11 = - 3 (рад/с).

Від’ємне значення кутової швидкості означає, що обертання диску здійснюється за стрілкою годинника і вектор кутової швидкості напрямлений від нас перпендикулярно площині рисунка (рис. 15).

Кутове прискорення обертального (переносного) руху ε_е знайдемо як похідну по часу від кутової швидкості

= ,

що, після підстановки на відповідного часу, дає

= 16 (рад/с² ).

Додатне значення кутового прискорення вказує, що вектор кутового прискорення обертання диску напрямлений до нас перпендикулярно площині рисунка, тобто швидкість обертання на даний момент часу сповільнюється.

Визначаємо модулі всіх сил інерції. Оскільки , , та , послідовно знайдемо модуль сили інерції нерівномірного обертання

= 2·16·2 = 64 (Н),

модуль відцентрової сили

= 2·3²·2 = 36 (Н),

та модуль сили інерції Коріолиса

= 2·2·3·3 = 36 (Н).

Напрями всіх сил інерції визначимо за правилами визначення напряму векторного добутку (дивись рис. 12).

Відповідь: = 64 Н, = 36 Н, = 36 Н.