Тема 4. Інтегрування диференціального рівнянь руху матеріальної точки, на яку діє сила, що залежить від координати

Диференціальне рівняння руху точки в цьому випадку має вигляд

. (1)

з початковими умовами: при = 0: , .

Якщо сила залежить лише від положення точки, то кожна декартова проекція сили залежить лише від відповідної проекції радіус-вектора, і рівняння (1) розкладається на три скалярні. В випадку одномірного руху точки диференціальне рівняння, наприклад, для - компоненти має вигляд

. (2)

Далі для спрощення записів будемо опускати індекси. Безпосередньо розділити змінні в такому рівнянні не вдається, тому виконаємо наступні перетворення

. (3)

Тоді, після розділу змінних, диференціальне рівняння приймає вигляд

, (4)

звідки, після інтегрування, отримуємо , або

. (5)

Враховуючи що , з (5) отримуємо

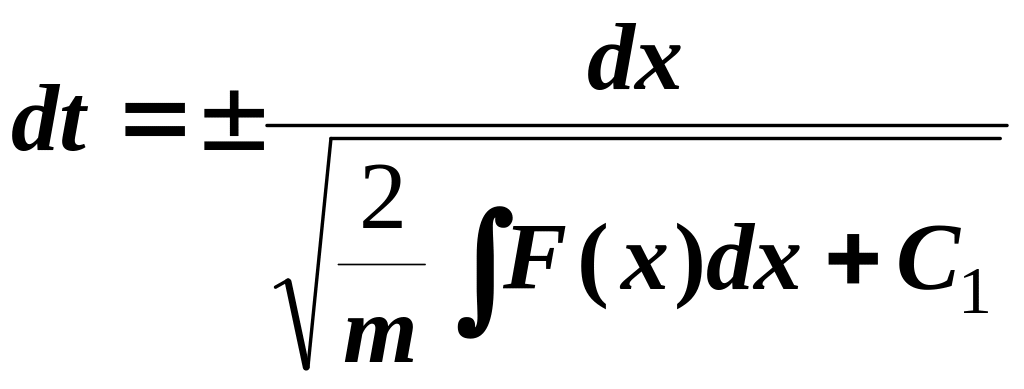. (6)

Проводячи повторне інтегрування, знаходимо

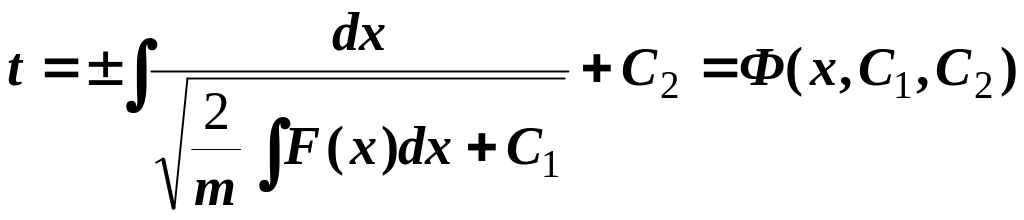. (7)

(Зауважимо, що в загальному випадку в рівнянні (7) виникають складні інтеграли, але в випадках, коли = 0, інтегрування не викликає труднощів.)

Розв’язуючи рівняння (7) відносно координати , знайдемо її залежність від часу та постійних інтегрування

. (8)

Задача дт.5. Інтегрування диференціального рівнянь руху матеріальної точки, на яку діє сила, що залежить від координати

Знайти закон руху тіла масою кг, за заданою силою Н та відповідними початковими умовами, які приведені у таблиці 5.

Таблиця 5

Вихідні дані для задачі ДТ.5

№	, кг	, Н	, м	, м/с	№	, кг	, Н	, м	, м/с
1	4		1	0,5	16	7		2	1
2	5		2		17	1		2	4
3	3		4	4	18	4		1	2
4	2		1	1	19	4		1	1
5	2		1	1	20	5		7	7
6	1		1	1	21	4		1	1
7	4		1	1	22	2		1	1
8	1		2	4	23	3		2	4
9	2/3			3	24	2		2	4
10	8		2	1	25	5		1	2
11	2		3	3	26	2		1	2
12	2		1	0,5	27	2		1
13	3		1	1	28	3		4	4
14	2		2	4	29	3		1
15	3		1	1	30	2		1