Задача дт.3. Інтегрування диференціального рівняння руху матеріальної точки, на яку діють сталі сили
В
аріанти
1, 4, 7, 10, 13, 16, 19, 22, 25, 28:
Мотоцикл під дією сталої сили
піднімається
с по ділянці
довжиною
,
яка складає з горизонтом кут
(рис. 1). Мотоцикл має в точці
швидкість
.
В точці
він досягає швидкості
,
перелітає через рів шириною
і через
с приземляється в точці
,
маючи швидкість
.
Маса мотоцикла з мотоциклістом
.
При розв’язку задачі мотоцикл з
мотоциклістом вважати матеріальною
точкою, нехтувати тертям кочення та
силою опору повітря.
Варіант
№ 1.
Дано:
= 30°;
= 400 кг,
= 2,2 кН;
= 0;
= 40 м;
= 5 м. Знайти
та
.
Варіант
№ 4.
Дано:
= 30°;
0;
= 40 м;
= 0;
= 4,5 м/с;
= 3 м. Знайти
та
.
Варіант № 7. Дано: = 30°; = 0; = 2 кН; = 50 м; = 2 м; = 4 м. Знайти та .
Варіант № 10. Дано: = 30°; = 0; = 40 м; = 4,5 м/с; = 2,5 м. Знайти та .
Варіант № 13. Дано: = 30°; = 400 кг, = 0; = 20 с; =3 м; = 1,5 м. Знайти та .
Варіант № 16. Дано: = 30°; 0; = 40 м; = 0; = 4,5 м/с; = 3 м. Знайти та .
Варіант № 19. Дано: = 30°; = 0; = 45 м; = 5,5 м/с; = 2,0 м. Знайти та .
Варіант № 22. Дано: = 30°; = 400 кг, = 0; = 20 с; = 3 м; = 1,5 м. Знайти та .
Варіант № 25. Дано: = 30°; = 350 кг, = 2,0 кН; = 0; = 45 м; = 7 м. Знайти та .
Варіант № 28. Дано: = 30°; = 0; = 2,4 кН; = 50 м; =3 м; = 5 м. Знайти та .
Варіанти
2, 5, 8, 11, 14, 17, 20, 23, 26, 29:
Тіло рухається з точки
по ділянці
довжиною
,
яка складає з горизонтом кут
.
Його початкова швидкість
,
а коефіцієнт тертя ковзання на ділянці
дорівнює
(рис. 2). Через
с в точці
воно покидає похилу площину зі швидкістю
і падає на горизонтальну площину в точці
,
маючи швидкість
,
перебуваючи в повітрі
с.
При розв’язку задачі тіло вважати матеріальною точкою масою та нехтувати силою опору повітря.
Варіант № 2. Дано: = 0; = 30°; = 0,2; = 6 м; = 4,5 м. Знайти та .
Варіант № 5. Дано: = 30°; = 0,1; = 1 м/с; = 1,5 с; = 10 м. Знайти та .
Варіант № 8. Дано: = 0; = 0; = 9,81 м; = 2 с; = 20 м. Знайти та .
Варіант
№ 11.
Дано:
= 0;
= 45°;
= 10 м;
= 2 с. Знайти
та рівняння траєкторії на ділянці
.
Варіант № 14. Дано: = 0; = 30°; = 0,2; = 10 м; = 12 м. Знайти та
Варіант № 17. Дано: = 30°; = 0,15; = 1,5 м/с; = 2,0 с; = 12 м. Знайти та .
Варіант № 20. Дано: = 0; = 45°; = 10 м; = 2 с. Знайти та рівняння траєкторії на ділянці .
Варіант № 23. Дано: = 0; = 0; = 5,5 м; = 1,5 с; = 20 м. Знайти та .
Варіант № 26. Дано: = 0; = 30°; = 0,2; = 10 м; = 12 м. Знайти та
Варіант № 29. Дано: = 0; = 30°; = 0,15; = 6 м; = 5,5 м. Знайти та .
Варіанти 3, 6, 9, 12, 15, 18, 21, 24, 27, 30: Лижник підходить до точки трампліна довжиною , який складає з горизонтом кут , зі швидкістю (рис. 3). Коефіцієнт тертя ковзання на ділянці дорівнює . Лижник від до рухається с і в точці зі швидкістю він покидає трамплін. Через с лижник приземляється зі швидкість в точці гори, яка складає кут з горизонтом.
В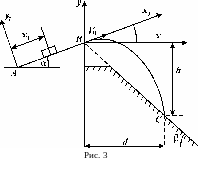
аріант
№ 3.
Дано:
= 20°;
= 0,1;
= 16 м/с;
= 5 м;
= 60°. Знайти
та
Варіант № 6. Дано: = 15°; = 0,15; = 0,2 с; = 40 м; = 30°. Знайти та .
Варіант № 9. Дано: = 18 м/с; = 0; = 0,3 с; = 15 м/с; = 60°. Знайти та .
Варіант № 12. Дано: = 15°; = 0; = 12 м/с; = 50 м; = 60°. Знайти та рівняння траєкторії лижника на ділянці .
Варіант
№ 15.
Дано:
= 15°;
= т0,3 с;
= 0,1;
42 м;
=45°. Знайти
та
.
Варіант № 18. Дано: = 20°; = 0,1; = 0,2 с; = 40 м; = 30°. Знайти та .
Варіант № 21. Дано: = 15°; = 0,1; = 16 м/с; = 5 м; = 45°. Знайти та .
Варіант № 24. Дано: = 21 м/с; = 0; = 0,3 с; = 20 м/с; = 60°. Знайти та .
Варіант
№ 27.
Дано:
= 15°;
= 0,3 с;
= 0,1;
м;
= 30°. Знайти
та
.
Варіант № 30. Дано: =15°; = 0; = 12 м/с; = 50 м; = 60°. Знайти та рівняння траєкторії лижника на ділянці .
Приклад.
Тіло рухається з точки
похилої площини маючи початкову швидкість
12 м/с. Коефіцієнт тертя ковзання
0,1, кут нахилу площини до горизонту
. Через
0,5 с тіло покидає похилу площину і падає
на горизонтальну площину в точці
(рис.
4).
Визначити
довжину
похилої площини, швидкість точки
в кінці похилої площини, а також координати
(
)
точки падіння, швидкість тіла в момент
падіння
тіла на горизонтальну площину, та кут
падіння.
Розв’язок.
Розглянемо рух тіла по похилій площині.
Приймаємо тіло за матеріальну точку,
на яку діють сили: вага
,
нормальна
реакція
N
та
сила тертя ковзання
.
Рівняння руху точки має вид
. (1)
Р
озташуємо
початок декартової системи координат
в точці
,
спрямувавши вісь
вздовж площини
(рис. 4), і отримуємо відповідні скалярні
рівняння для сил, що діють вздовж цих
напрямів:
, (2)
, (3)
отже
.
Оскільки
,
перепишемо (2) в наступному вигляді
,
де
м/с.
Інтегруючи двічі останнє диференційне рівняння, отримуємо:
,
.
Для
визначення сталих інтегрування
,
та
скористаємося
початковими умовами:
0,
,
і отримуємо:
,
= 0,
Тоді,
остаточно, для координати тіла
та його швидкості
на першому етапі руху маємо:
, (4)
. (5)
Ці рівняння дозволяють визначити швидкість тіла в момент часу , коли тіло покидає похилу площину та довжину похилої площини:
(м/с), (6)
(м). (7)
Далі розглянемо рух тіла від точки до точки падіння . На цій ділянці діє лише сила тяжіння тому диференціальне рівняння руху має вид
.
Розташуємо
початок нової декартової системи
координат
в точці
(рис. 4), спрямувавши вісі відповідно
горизонтально та вертикально вгору, і
тоді отримуємо наступні диференціальні
рівняння руху на другій ділянці руху:
,
. (8)
Початкові умови на цій ділянці наступні:
,
7,8 (м/с),
4,5 (м/с).
Двічі інтегруємо диференціальні рівняння (8) і послідовно отримаємо:
,
,
,
.
Запишемо отримані рівняння для моменту часу = 0:
,
,
,
,
і знайдемо з них сталі інтегрування:
,
(м/с),
(м/с).
Таким чином, рівняння для визначення координат та компонент швидкості на другої ділянці руху набувають вигляду:
(м/с),
(м/с),
(м),
(м).
Точка падіння тіла на площину (дивись рис. 1) має координату
(м),
що дозволяє записати рівняння для визначення часу руху тіла та ділянці
,
розв’язок
якого дає
с.
Цей час дозволяє визначити - координату точці падіння тіла
(м),
компоненти швидкості:
(м/с),
(м/с),
і також модуль швидкості в точці падіння
(м/с).
Кут з горизонтом (під яким тіло падає на площину) знайдемо з геометричних міркувань (дивись рис. 4)
,
що дає
.
Відповідь:
= 5,25 м,
м/с,
м,
м,
м/с,