
- •Подільський державний аграрно - технічний університет
- •Кафедра загальнотехнічних дисциплін і фізики методичні вказівки
- •Динаміка
- •Розділ 1. Динаміка точки Тема 1. Пряма задача динаміки
- •Контрольні запитання
- •Задача дт.1. Визначення сили за відомим законом руху точки
- •Тема 2. Інтегрування диференціального рівнянь руху матеріальної точки, яка знаходиться під дією сталих сил
- •Задача дт.2. Інтегрування диференціального рівняння руху матеріальної точки, на яку діє сила тяжіння
- •Задача дт.3. Інтегрування диференціального рівняння руху матеріальної точки, на яку діють сталі сили
- •Тема 3. Інтегрування диференціального рівнянь руху матеріальної точки, на яку діє сила, що залежить від часу
- •Задача дт.4. Інтегрування диференціального рівнянь руху матеріальної точки, на яку діє сила, що залежить від часу
- •Тема 4. Інтегрування диференціального рівнянь руху матеріальної точки, на яку діє сила, що залежить від координати
- •Задача дт.5. Інтегрування диференціального рівнянь руху матеріальної точки, на яку діє сила, що залежить від координати
- •Тема 5. Відносний рух точки. Сили інерції
- •Контрольні запитання
- •Задача дт.6. Динаміка відносного руху точки
- •Тема 6. Механічні коливання а) Вільні (власні) коливання з одним ступенем свободи
- •Контрольні запитання
- •Б) Вільні згасаючі коливання з одним ступенем свободи
- •Контрольні запитання
- •В) Змушені коливання з одним ступенем свободи
- •Контрольні запитання
- •Задача дт.7. Дослідження одномірних вільних, згасаючих та змушених коливань
- •Розділ 2. Динаміка механічної системи
- •Тема 1. Рух центра мас механічної системи
- •Контрольні запитання
- •Задача дс.1. Дослідження руху центру мас механічної системи
- •Тема 2. Теорема про зміну та збереження імпульсу механічної системи
- •Контрольні запитання
- •Задача дс.2. Застосування теореми про зміну імпульсу для дослідження руху механічної системи
- •Тема 3. Теорема про зміну та збереження моменту імпульсу механічної системи
- •Контрольні запитання
- •Задача дс.3. Застосування теореми про зміну моменту імпульсу для визначення кутової швидкості механічної системи
- •Тема 4. Теорема про зміну кінетичної енергії механічної системи
- •Контрольні запитання
- •Задача дс.4. Застосування теореми про зміну кінетичної енергії механічної системи
- •Тема 5. Динаміка поступального, обертального та плоского рухів системи тіл
- •Контрольні запитання
- •Задача дс.5. Динаміка поступального, обертального та плоского рухів системи тіл
- •Тема 6. Фізичний маятник
- •Контрольні запитання
- •Задача дс.6. Визначення періоду коливань фізичного маятника
- •Література
Тема 6. Фізичний маятник
Ф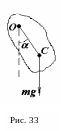 ізичний
маятник – це будь-яке тіло, яке закріплене
(підвішене) у точці, яка не співпадає з
центром його маси, та має можливість
здійснювати коливання навколо цієї
точки.
ізичний
маятник – це будь-яке тіло, яке закріплене
(підвішене) у точці, яка не співпадає з
центром його маси, та має можливість
здійснювати коливання навколо цієї
точки.
Розглянемо
таке тіло, яке закріплено в точці О,
та відхилене від положення рівноваги
на кут
![]() (рис. 33). В цьому випадку сила тяжіння
(рис. 33). В цьому випадку сила тяжіння
![]() ,
яка прикладена до центру маси тіла
(точка С)
створює момент сили відносно точки
закріплення О
,
яка прикладена до центру маси тіла
(точка С)
створює момент сили відносно точки
закріплення О
![]() .
(1)
.
(1)
Цей момент намагається повернути тіло навколо точки підвісу до положення рівноваги (проти кута відхилення ). Таким чином, основне рівняння обертального руху може бути записано в вигляді:
![]() ,
(2)
,
(2)
де
![]() - момент інерції тіла відносно точки
підвісу.
- момент інерції тіла відносно точки
підвісу.
Отримали
нелінійне диференціальне рівняння,
розв’язок якого є окремою математичною
задачею. Одначе для малих кутів відхилення
![]() ,
тоді рівняння (2) зводиться до відомого
рівняння гармонічних коливань
,
тоді рівняння (2) зводиться до відомого
рівняння гармонічних коливань
![]() . (3)
. (3)
в якому
![]() , (4)
, (4)
- кругова частота коливань, з якою зв’язаний період коливань
![]() . (5)
. (5)
Таким
чином, щоб знайти частоту (чи період)
коливань фізичного маятника, треба
знайти масу тіла
,
відстань
![]() між точкою закріплення та центром маси
тіла, та момент інерції тіла
між точкою закріплення та центром маси
тіла, та момент інерції тіла
![]() відносно точки закріплення.
відносно точки закріплення.
Контрольні запитання
1. За якої умови фізичний маятник здійснює гармонічні коливання?
2. Запишіть рівняння гармонічних коливань фізичного маятника.
3. Запишіть розв’язок рівняння гармонічних коливань фізичного маятника.
4. Від яких величин залежить амплітуда коливань, частота коливань?
Задача дс.6. Визначення періоду коливань фізичного маятника
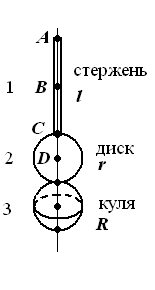
Визначити період коливань фізичного маятника (рис. 34 - 42). Маси (в кг) та геометричні розміри елементів маятника (в м) наведені в таблиці 6.
Таблиця 6
Вихідні дані для задачі ДС.6
№ |
m1 |
R,r,l, |
m2, |
R,r,l, |
m3, |
R,r,l, |
рис |
підвіс |
|
№ |
m1 |
R,r,l, |
m2, |
R,r,l, |
m3, |
R,r,l, |
Рис |
підвіс |
1 |
1 |
0,18 |
1 |
0,19 |
4 |
0,75 |
34 |
A |
|
16 |
1 |
0,85 |
2 |
0,13 |
4 |
0,14 |
40 |
A |
2 |
2 |
0,11 |
3 |
0,14 |
6 |
0,65 |
35 |
B |
|
17 |
3 |
0,6 |
3 |
0,16 |
7 |
0,11 |
41 |
B |
3 |
2 |
0,13 |
5 |
0,13 |
12 |
0,65 |
36 |
C |
|
18 |
4 |
0,7 |
4 |
0,13 |
11 |
0,18 |
42 |
C |
4 |
2 |
0,2 |
5 |
0,15 |
11 |
0,9 |
37 |
D |
|
19 |
3 |
0,65 |
3 |
0,19 |
7 |
0,15 |
34 |
D |
5 |
4 |
0,2 |
1 |
0,23 |
9 |
0,6 |
38 |
A |
|
20 |
4 |
0,8 |
4 |
0,18 |
9 |
0,2 |
35 |
A |
6 |
2 |
0,23 |
3 |
0,11 |
6 |
0,65 |
39 |
B |
|
21 |
2 |
0,8 |
1 |
0,19 |
4 |
0,23 |
36 |
B |
7 |
4 |
0,13 |
5 |
0,14 |
14 |
0,9 |
40 |
C |
|
22 |
1 |
0,75 |
3 |
0,14 |
6 |
0,15 |
37 |
D |
8 |
3 |
0,21 |
5 |
0,14 |
9 |
0,7 |
41 |
D |
|
23 |
3 |
0,11 |
2 |
0,95 |
7 |
0,18 |
38 |
A |
9 |
5 |
0,65 |
3 |
0,6 |
13 |
0,85 |
42 |
A |
|
24 |
3 |
0,11 |
3 |
0,75 |
7 |
0,13 |
39 |
B |
10 |
4 |
0,8 |
1 |
0,4 |
7 |
0,85 |
34 |
B |
|
25 |
1 |
0,15 |
4 |
1 |
8 |
0,2 |
40 |
C |
11 |
1 |
0,8 |
4 |
0,4 |
6 |
0,95 |
35 |
C |
|
26 |
3 |
0,19 |
3 |
0,9 |
7 |
0,2 |
41 |
D |
12 |
4 |
0,7 |
3 |
0,1 |
9 |
0,85 |
36 |
D |
|
27 |
4 |
0,23 |
5 |
0,7 |
10 |
0,19 |
42 |
A |
13 |
4 |
1 |
1 |
0,1 |
9 |
0,75 |
37 |
A |
|
28 |
2 |
0,23 |
2 |
0,55 |
8 |
0,14 |
34 |
B |
14 |
1 |
0,85 |
3 |
0,8 |
7 |
0,55 |
38 |
B |
|
29 |
5 |
0,13 |
1 |
0,9 |
10 |
0,14 |
35 |
C |
15 |
5 |
0,65 |
4 |
0,1 |
12 |
0,75 |
39 |
C |
|
30 |
3 |
0,19 |
1 |
0,9 |
6 |
0,23 |
36 |
D |
Рис. |
Рис.
|
Рис.
|
Рис. |
Рис. |
Рис. |
Рис. |
Рис. |
Рис.
|
П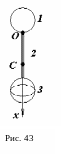 риклад.
риклад.
Фізичний маятник здійснює коливання відносно осі, яка проходить перпендикулярно рисунку через точку О (рис. 43). Записати рівняння вільних коливань цього маятника та визначити період цих коливань. Тіло 1 є однорідний диск масою = 4 кг та радіуса = 0,4 м, тіло 2 – однорідний стрижень масою = 3 кг та довжиною = 0,8 м, тіло 3 – однорідна куля масою = 4 кг та радіуса = 0,4 м.
Розв’язок.
Диференціальне рівняння коливань фізичного маятника може бути записано без будь-яких труднощів згідно (3):
![]() ,
,
де
.
Визначимо необхідні дані для розрахунків кругової частоти (періоду) коливань: масу маятника m; відстань ОС між віссю обертання (точкою закріплення) та центром маси і момент інерції тіла J відносно осі обертання.
Маса фізичного маятника є сума мас його елементів
![]() =
4 + 3 + 4 = 11 (кг).
=
4 + 3 + 4 = 11 (кг).
Щоб підрахувати відстань ОС скористуємось визначенням центру мас
![]() ,
,
та розмістимо початок відліку координатної осі х в точці закріплення, а вісь х спрямуємо вниз, як це зроблено на рис. 43. Тоді
![]() (м).
(м).
Момент інерції маятника відносно осі обертання є сума моментів інерції його елементів відносно цієї осі
![]() ,
,
де
![]() - моменти інерції диску, стрижня та кулі
відносно осі обертання. Ці моменти
інерції знайдемо скориставшись теоремою
Гюйгенса-Штейнера
- моменти інерції диску, стрижня та кулі
відносно осі обертання. Ці моменти
інерції знайдемо скориставшись теоремою
Гюйгенса-Штейнера
![]() ,
,
де
![]() - момент інерції тіла відносно осі, яка
проходить через центр маси відповідного
тіла паралельно осі обертання, а
- момент інерції тіла відносно осі, яка
проходить через центр маси відповідного
тіла паралельно осі обертання, а
![]() - відстань між центром маси тіла та віссю
обертання. Моменти інерції більшості
тіл правильної форми можна знайти у
довідниках з фізики чи математики, а
також у додатку.
- відстань між центром маси тіла та віссю
обертання. Моменти інерції більшості
тіл правильної форми можна знайти у
довідниках з фізики чи математики, а
також у додатку.
Отож, для диску маємо
![]() =
=
![]() = 0,96 (кг·м2),
= 0,96 (кг·м2),
для стрижня
![]() =
=
![]() = 0,64 (кг·м2),
= 0,64 (кг·м2),
для кулі
![]() =
=
![]() = 6,016 (кг·м2).
= 6,016 (кг·м2).
Таким чином момент інерції маятника
![]() = 0,96 + 0,64 + 6,016 = 7,616 (кг·м2).
= 0,96 + 0,64 + 6,016 = 7,616 (кг·м2).
Отримані дані дозволяють визначити період коливань маятника:
![]() = 2,64
с
= 2,64
с
Відповідь: Т = 2,64 с.

 34
34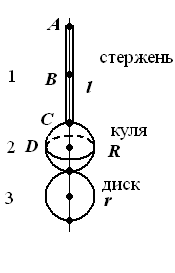 35
35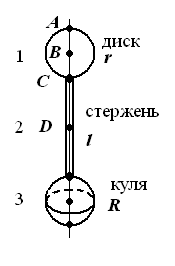 36
36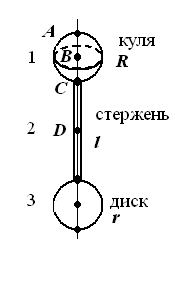 37
37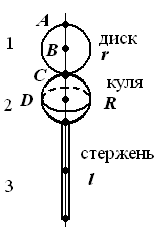 38
38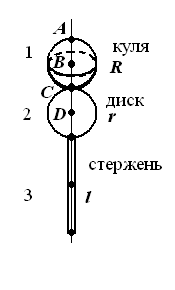 39
39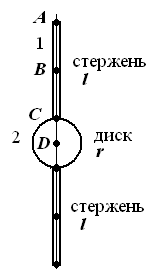 40
40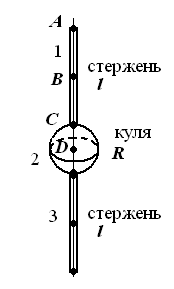 41
41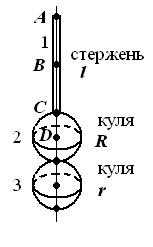 42
42