Контрольні запитання

1. Чому дорівнює кінетична енергія матеріальної точки?

2. Якою швидкістю (абсолютною, переносною чи відносною) визначається кінетична енергія матеріальної точки?

3. Як залежить від часу кінетична енергія точки, яка здійснює рівнозмінний рух з нульової початковою швидкістю?

4. Запишіть вираз для кінетичної енергії твердого тіла, яке здійснює:

а) поступальний рух,

б) обертальний рух,

в) плоский рух.

5. Як підрахувати кінетичну енергію механічної системи?

6. Два тіла обертається навколо нерухомих осей так, що їх моменти імпульсу відносно цих осей однакові. Чи є рівними кінетичні енергії тіл, якщо їх моменти інерції різні ( )?

7. Як визначити елементарну роботу сили? В яких випадках вона додатна, від’ємна, дорівнює нулю?

8. Вкажіть сили, для яких робота сили при кінцевому переміщенні точки не залежить від траєкторії. Як такі сили називаються?

9. Вкажіть сили, для яких робота сили при кінцевому переміщенні точки залежить від траєкторії. Як такі сили називаються?

10. Як повинна рухатись система матеріальних точок, щоб сума робіт сил тяжіння для цієї системи дорівнювала нулю?

11. Як визначається робота пружної сили?

12. В яких випадках робота сили, яка прикладена до тіла що здійснює обертальний рух дорівнює нулю?

13. В яких механічних системах сума робіт внутрішніх сил дорівнює нулю?

Задача дс.4. Застосування теореми про зміну кінетичної енергії механічної системи

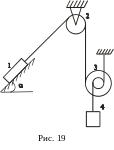
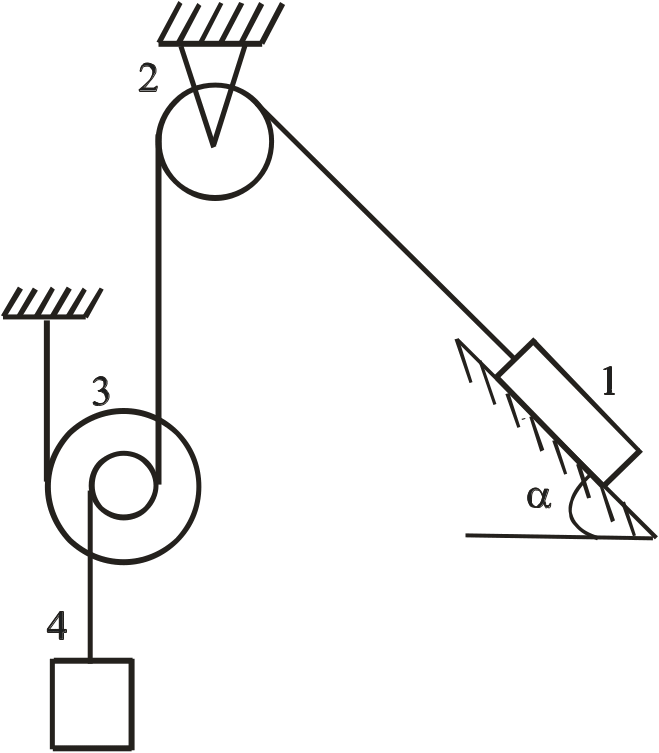
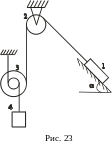
Механічна система (рис. 16 - 23) починає рухатись зі стану спокою під дією сил тяжіння. Знайти швидкість та прискорення тіла 1 на момент часу, коли воно пройде шлях , користуючись теоремою про зміну кінетичної енергії. Маси, моменти інерції та розміри тіл, які входять до системи наведені в таблиці 4 .

Таблиця 4 – вихідні дані для задачі ДС.4

№	рис	, кг	, кг	, кг	, кг		, м	, м	, кг·м2	, м	, м	, кг·м2	, градус	, м
1	16	18	3	2	1	0,1	0,3	0,2	0,12	0,2	-	0,04	45	2
2	17	24	4	3	2	0,2	0,25	-	0,13	0,3	0,2	0,18	60	3
3	18	42	2	4	3	0,15	0,3	-	0,08	0,4	0,3	0,25	75	4
4	19	30	4	5	3	0,1	0,2	-	0,08	0,2	0,1	0,09	60	3
5	20	35	3	4	2	0,2	0,2	0,1	0,015	0,5	-	0,35	45	1,2
6	21	28	5	3	1	0,15	0,5	-	0,8	0,3	0,2	0,12	70	1,5
7	22	35	4	2	3	0,1	0,3	-	0,18	0,4	0,3	0,24	60	4
8	23	42	3	5	2	0,2	0,1	-	0,012	0,5	0,25	0,8	75	2,4
9	16	48	2	4	3	0,15	0,3	0,15	0,09	0,3	-	0,25	45	3
10	17	32	3	2	1	0,2	0,1	-	0,015	0,2	0,15	0,07	60	1
11	18	42	4	3	2	0,1	0,2	-	0,08	0,4	0,2	0,27	75	2
12	19	34	2	4	3	0,12	0,1	-	0,01	0,3	0,15	0,25	45	3
13	20	32	3	2	2	0,15	0,2	0,1	0,06	0,4	-	0,24	60	4
14	21	44	4	3	1	0,2	0,3	-	0,18	0,3	0,1	0,12	75	3
15	22	46	3	4	3	0,1	0,1	-	0,016	0,2	0,1	0,09	45	2
16	23	3	2	4	24	0,12	0,2	-	0,05	0,3	0,15	0,16	30	4
17	16	2	4	3	25	0,15	0,4	0,2	0,025	0,4	-	0,30	15	1
18	17	4	3	2	22	0,1	0,3	-	0,14	0,2	0,15	0,06	40	2
19	18	4	2	3	32	0,2	0,15	-	0,03	0,3	0,2	0,18	15	1,5
20	19	2	3	4	28	0,1	0,25	-	0,1	0,4	0,3	0,5	40	2,5
21	20	4	2	3	26	0,15	0,4	0,2	0,18	0,3	-	0,14	30	3
22	21	3	4	2	16	0.1	0,35	-	0,2	0,2	0,1	0,04	20	2,5
23	22	2	3	4	18	0,2	0,25	-	0,1	0,3	0,15	0,25	30	1,5
24	23	4	2	3	20	0,15	0,15	-	0,03	0,4	0,3	0,35	35	2
25	16	3	4	2	22	0,12	0,3	0,1	0,16	0,5	-	0,32	40	3
26	17	2	3	4	24	0,2	0,15	-	0,09	0,4	0,3	0,5	45	2
27	18	4	2	3	30	0,1	0,25	-	0,07	0,2	0,1	0,07	30	1,3
28	19	2	4	3	32	0,2	0,3	-	0,2	0,5	0,3	0,48	45	1,8
29	20	4	3	2	24	0,1	0,2	0,1	0,06	0,4	-	0,18	15	1,5
30	21	3	2	4	26	0,12	0,15	-	0,03	0,3	0,1	0,10	30	3

	Рис. 17
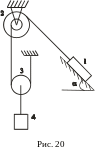
	Рис. 21

П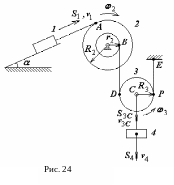 риклад: Механічна система (рис. 24) починає рухатись зі стану спокою під дією сил тяжіння. Знайти швидкість та прискорення тіла 1 на момент часу, коли воно пройде шлях , користуючись теоремою про зміну кінетичної енергії.

Розв’язок. Будемо вважати, що тіло 1 починає рух у напрямку праворуч догори і на момент, коли воно пройде шлях S₁, набуває швидкості v₁.

Згідно з теоремою про зміну кінетичної енергії, ця зміна дорівнює роботі зовнішніх сил

, (1)

де - кінетична енергія системи на даний момент часу, - початкова кінетична енергія системи. Оскільки в початковому стані система нерухома , то

. (2)

Тіло 2 в цей момент часу буде обертатися за стрілкою годинника з певною кутовою швидкістю , тіло 3 буде здійснювати плоскопаралельний рух, обертаючись проти стрілки годинника з кутовою швидкістю , а його центр (вісь обертання блоку) буде рухатись вниз з певною швидкістю . Тіло 4 буде рухатись теж вниз і, оскільки воно закріплено до осі блоку 3, його лінійна швидкість (рис. 24).

Підрахуємо кінетичну енергію системи на момент часу, коли тіло 1, пройде шлях , як суму кінетичних енергій її компонентів

, (3)

де:

, (4)

, (5)

, (6)

. (7)

Щоб знайти кінетичну енергію системи як функцію швидкості першого тіла, проведемо кінетичний аналіз механізму, і встановимо зв’язок між лінійними та кутовими характеристиками руху різних елементів механічної системи.

Легко бачити, що точка А блоку 2 має також саму лінійну швидкість, що і тіло 1, і зв’язок лінійної швидкості з кутовою швидкістю блока 2 очевидний

. (8)

В такому випадку лінійна швидкість точки В (як і точки D) знайти як

. (9)

Щоб знайти лінійну швидкість та кутову швидкість , скористуємось тою обставиною, що тіло 3 здійснює плоскопаралельний рух з ненульовою кутовою швидкістю, і, у цьому випадку має миттєвий центр швидкості (МЦШ), який розташовано в точці Р. Тоді

,

звідки, з урахуванням (9), можна отримати вираз для

. (10)

Швидкість центру блока 3 (одночасно і швидкість тіла 4) отримаємо з співвідношення

. (11)

Просумуємо (4) - (8) з урахуванням кінематичних зв’язків (8), (10), (11)

. (12)

Знайдемо роботу зовнішніх сил як суму робот окремих сил:

. (13)

В нашому випадку зовнішніми силами є сили тяжіння: , , , , нормального тиску , та тертя .

Оскільки сила опору перпендикулярна переміщенню її робота дорівнює нулю. Сила тертя протилежна переміщенню і її робота від’ємна

. (14)

Складова сили тяжіння вздовж вектора переміщення дорівнює , і, оскільки ці вектори протилежні за напрямом, робота сил тяжіння для переміщення першого тіла теж від’ємна

. (15)

Зауважимо, що такий самий результат ми отримаємо з того факту, що перше тіло рухається догори (проти сили тяжіння) і робота сили тяжіння у цьому випадку від’ємна – доведіть це самі.

Оскільки друге тіло не змінює свого положення внаслідок дії зовнішніх сил та , робота цих сил дорівнює нулю.

Центри мас третього та четвертого тіл зміщуються вертикально додолу під дією сил та відповідно, отож:

, . (16)

Очевидно, що в нашому випадку , а зв’язок з знайдемо з кінематичного аналізу механізму. Вище ми показали (11), що . Оскільки, за визначенням, , то, інтегруючи (11), легко отримаємо

. (17)

Підставляючи (17) в (16), та сумуючи (14) - (16), отримаємо

. (18)

Оскільки зміна кінетичної енергії (12) дорівнює роботі зовнішніх сил (18), то

=

= ,

звідки знаходимо вираз, який визначає швидкість тіла 1

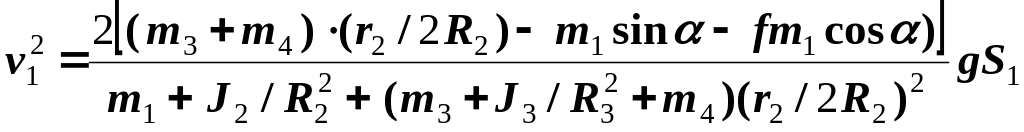. (19)

Якщо в результаті розрахунків отримуємо , то потрібно змінити напрями руху тіл 1, 3, 4 та обертання тіла 4. При цьому у формулах (15) - (16) необхідно внести відповідні зміни щодо роботи сил тяжіння, що приведе до наступних змін у кінцевій формулі (19): в чисельнику зміняться знаки при масах тіл 1, 3 та 4 і зміниться знак при коефіцієнті тертя f, бо сила тертя ковзання завжди напрямлена проти напряму руху тіла і отримуємо

. (20)

Якщо і цьому випадку знову отримуємо , то система зберігає стан спокою за рахунок дії сил тертя ковзання.

Прискорення першого тіла знайдемо, взявши похідну за часом від (19)

=

= ,

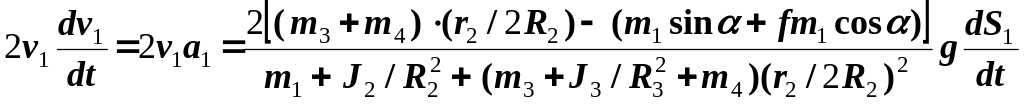звідки

. (21)

Відповідь: ,

.
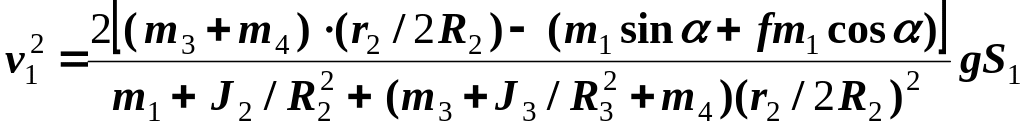