Тема 4. Теорема про зміну кінетичної енергії механічної системи

Величина, яка характеризує рух тіла, називається кінетичною енергією.

1. Якщо тверде тіло здійснює поступальний рух, то швидкості всіх його точок однакові v = const і його кінетична енергія визначається як половина добутку маси тіла на квадрат його швидкості

. (1)

2. Якщо тверде тіло обертається довкола нерухомої осі (наприклад, z) з кутовою швидкістю , то кінетична енергія дорівнює половині добутку моменту інерції тіла відносно осі обертання на квадрат кутової швидкості

, (2)

де I_z - момент інерції твердого тіла відносно осі обертання.

3. Якщо тверде тіло здійснює складний рух, то його рух можна розглядати як накладання двох простих рухів – поступального зі швидкістю руху центру мас та обертального руху з кутовою швидкістю навколо миттєвої осі обертання, що проходить через центр мас. Тоді

. (3)

У випадку плоского руху твердого тіла вектор перпендикулярний до площини руху і легко отримати відповідну енергію

, (4)

де - швидкість довільно обраної точки твердого тіла, I_zC - момент інерції тіла відносно осі z, яка проходить крізь цю точку перпендикулярно до площини руху.

Зауважимо, що коли матеріальна система складається з декількох тіл, то її кінетична енергія буде дорівнювати сумі кінетичних енергій всіх тіл, які входять в систему, тобто

T = T₁ + T₂ +…+ T_n = . (5)

Фізична величина, яку називають роботою, є міра передачі руху від одного тіла до іншого. Робота сили на скінченому переміщенні S між точками O та M буде:

. (6)

Розглянемо роботу конкретних сил, які можуть виникати в системі.

1. Робота сили тяжіння виконується силою тяжіння при переміщенні тіла (матеріальної точки) масою з положення 1 в положення 2. Ця робота не залежить від форми траєкторії, і визначається лише різницею кінцевого ( ) та початкового ( ) положень вздовж вертикалі

. (7)

2. Робота сили пружності при переході точки з положення де довжина пружини до положення, коли довжина стала , визначається виразом

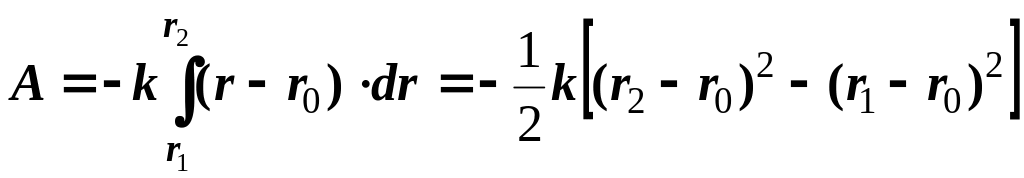, (8)

і також не залежить від траєкторії точки, а залежить лише від її кінцевих положень.

3. Робота сил, які прикладені до твердого тіла, що здійснює обертання довкола нерухомої осі при повороті тіла на кінцевий кут визначається рівнянням

, (9)

де момент зовнішньої сили відносно нерухомої осі, та початкове та кінцеве значення кута , яке визначає положення тіла.

4. Робота сил тертя ковзання. Оскільки сила тертя завжди направлена в бік, протилежний відносній швидкості, то робота сила тертя визначиться взятому зі знаком мінус добутку модуля сили тертя на довжину траєкторії

. (10)

5. Робота сил тертя кочення. Якщо тіло котиться без ковзання по поверхні іншого нерухомого тіла, сила тертя кочення створює момент і для роботи , отримуємо

, (11)

де - - коефіцієнт тертя кочення, а - кут, на який повернулося перше тіло.

Якщо в процесі свого руху матеріальна система перейшла з одного положення, яке вона займала в момент часу = 0, в інше положення, що відповідає моменту часу t, то можна отримати зв’язок між зміною кінетичної енергії та роботою сил, які прикладені до системи:

, (12)

де та - кінетична енергія матеріальної системи в кінцевому та початковому станах, а - повна робота, яку здійснюють при цьому переміщенні всі прикладені до системи внутрішні та зовнішні сили.

Рівняння (12) є записом теореми про зміну кінетичної енергії в інтегральній формі: зміна кінетичної енергії матеріальної системи за певний проміжок часу дорівнює сумі робіт внутрішніх та зовнішніх сил, які діють на точки системи на протязі даного проміжку часу.

Відмітимо, що у випадку, коли матеріальна система складається з абсолютно твердих тіл (тобто коли можна нехтувати деформаціями в цій системі), тоді під дією внутрішніх сил не відбувається зміщень частинок системи, тому сума робіт всіх внутрішніх сил абсолютно твердого тіла при любому його переміщенні дорівнює нулю і теорема приймає вигляд:

. (13)