Тема 2. Теорема про зміну та збереження імпульсу механічної системи
Імпульсом
механічної системи називається вектор
,
який дорівнює сумі імпульсів точок, що
входять до системи
. (1)
Похідна за часом від вектора імпульсу системи матеріальних точок дорівнює головному вектору всіх зовнішніх сил, які діють на систему
. (2)
Це є математичне формулювання теореми про зміну імпульсу механічної системи в диференціальній формі. Отримане векторне рівняння еквівалентне трьом скалярним:
,
,
. (3)
З доведеної теореми випливають наступні наслідки:
а) внутрішні сили безпосередньо не впливають на зміну імпульсу механічної системи;
б) якщо
головний вектор всіх зовнішніх сил, що
діють на систему, дорівнює нулю
,
то вектор імпульсу механічної системи
залишається постійним за величиною та
напрямом
=
, (4)
де
- початкове значення імпульсу системи.
Формула (4) є математичним записом закону
збереження імпульсу механічної системи;
в) якщо
проекція головного вектора всіх зовнішніх
сил, що діють на систему, на деяку нерухому
вісь, наприклад, вісь
,
дорівнює нулю, то проекція імпульсу
механічної системи на цю вісь залишається
постійною
, (5)
де
- початкове значення проекції імпульсу
.
Якщо головний
вектор всіх зовнішніх сил, що діють на
систему, не дорівнює нулю (
),
то зміна імпульсу механічної системи
за проміжок часу від
до
дорівнює інтегралу від головного вектора
зовнішніх сил, які прикладені до точок
системи, за той самий проміжок часу
, (6)
де
-
імпульс механічної системи в момент
часу
та
- в момент часу
.
Формула (6) є математичним записом теореми
про зміну імпульсу механічної системи
в інтегральній формі.
Контрольні запитання
1. Як змінюється імпульс матеріальної точки, яка рівномірно рухається по колу?
2. Чому рівно імпульс тіла, яке обертається навколо нерухомої осі, що проходить через його центр маси?
3. Сформулюйте теорему про зміну імпульсу механічної системи у диференціальній та інтегральній формах.
4. У яких випадках імпульс механічної системи або його проекція на вісь залишається сталою?
5. Чи може сила ваги змінити горизонтально складову кількості руху системи?
Задача дс.2. Застосування теореми про зміну імпульсу для дослідження руху механічної системи
Н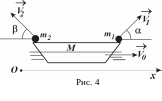
епарні
варіанти:
Човен масою М
кг рухається зі швидкістю V0
м/с. У певний момент часу курсанти, маси
яких
кг та
кг відповідно, стрибають одночасно з
човна зі швидкостями
та
м/с відносно човна. Перший курсантів
стрибає під кутом
°,
а другий - під кутом
°
до горизонту (рис. 4). Знайти кінцеву
швидкість човна. Додатний напрям стрибка
співпадає з початковим напрямом руху
човна. Силами тертя нехтувати та не
враховувати вертикальні коливання
човна.
П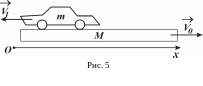
арні
варіанти:
По порому масою
,
який має швидкістю
м/с рухається автомобіль масою
зі швидкістю
м/с відносно порому (рис. 5). Автомобіль
починає змінювати швидкість. Знайти
швидкість порому на момент, коли відносна
швидкість автомобілю становить
м/с. Опором повітря та води нехтувати.
(Знаки швидкостей
та
вказані по відношенню до швидкості
платформи
).
Таблиця 2
Вихідні дані для задачі ДС.2
№ |
M |
|
m1 |
V1 |
° |
напрям |
m2 |
V2 |
° |
напрям |
1 |
250 |
4,0 |
65 |
7,0 |
15 |
- |
75 |
2,0 |
30 |
+ |
2 |
10000 |
3,0 |
2500 |
- 5,0 |
--- |
--- |
--- |
1,5 |
--- |
--- |
3 |
320 |
6,5 |
70 |
4,5 |
15 |
- |
60 |
1,0 |
30 |
- |
4 |
11000 |
3,5 |
3000 |
4,0 |
--- |
--- |
--- |
- 1,5 |
--- |
--- |
5 |
350 |
4,0 |
65 |
7,0 |
30 |
+ |
85 |
3,5 |
45 |
+ |
6 |
9500 |
5,5 |
1500 |
4,5 |
--- |
--- |
--- |
1,5 |
--- |
--- |
7 |
390 |
4,5 |
75 |
6,0 |
30 |
+ |
85 |
1,0 |
60 |
- |
8 |
12500 |
4,5 |
2500 |
- 4,0 |
--- |
--- |
--- |
- 1,0 |
--- |
--- |
9 |
290 |
5,0 |
90 |
5,0 |
60 |
- |
70 |
3,5 |
30 |
- |
10 |
1300 |
4,0 |
2000 |
3,0 |
--- |
--- |
--- |
- 1,5 |
--- |
--- |
11 |
310 |
3,0 |
85 |
5,0 |
45 |
- |
60 |
1,5 |
45 |
- |
12 |
11500 |
4,5 |
1500 |
1,0 |
--- |
--- |
--- |
4,0 |
--- |
--- |
13 |
290 |
6,5 |
65 |
6,5 |
45 |
- |
70 |
3,0 |
15 |
- |
14 |
10300 |
3,0 |
1700 |
- 1,5 |
--- |
--- |
--- |
4,0 |
--- |
--- |
15 |
320 |
4,5 |
75 |
5,0 |
0 |
- |
80 |
3,5 |
30 |
- |
16 |
12100 |
4,5 |
1900 |
1,0 |
--- |
--- |
--- |
4,5 |
--- |
--- |
17 |
410 |
6,5 |
75 |
5,0 |
45 |
- |
65 |
3,5 |
75 |
- |
18 |
11900 |
5,5 |
2100 |
- 4,5 |
--- |
--- |
--- |
- 1,0 |
--- |
--- |
19 |
340 |
6,5 |
65 |
4,0 |
0 |
+ |
80 |
1,5 |
30 |
+ |
20 |
10700 |
4,0 |
1300 |
3,5 |
--- |
--- |
--- |
1,0 |
--- |
--- |
21 |
360 |
5,5 |
85 |
5,0 |
0 |
- |
65 |
1,5 |
75 |
+ |
22 |
13300 |
5,0 |
2700 |
- 1,5 |
--- |
--- |
--- |
3,0 |
--- |
--- |
23 |
390 |
5,5 |
85 |
6,5 |
15 |
- |
70 |
3,5 |
45 |
- |
24 |
12600 |
4,5 |
2400 |
1,0 |
--- |
--- |
--- |
4,0 |
--- |
--- |
25 |
470 |
6,0 |
85 |
5,5 |
15 |
- |
60 |
2,5 |
30 |
- |
26 |
12500 |
4.5 |
2500 |
3,0 |
--- |
--- |
--- |
- 1,5 |
--- |
--- |
27 |
420 |
7,0 |
80 |
6,0 |
60 |
- |
75 |
2,5 |
45 |
- |
28 |
14000 |
3,5 |
3000 |
- 1,0 |
--- |
--- |
--- |
- 4,5 |
--- |
--- |
29 |
290 |
4,0 |
65 |
4,0 |
45 |
- |
75 |
2,0 |
15 |
- |
30 |
12300 |
5,0 |
2700 |
4,0 |
--- |
--- |
--- |
0 1,0 |
--- |
--- |
П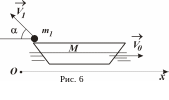
риклад
1.
Човен
масою М
= 200 кг на якому знаходиться курсант
масою
=
70 кг рухається зі швидкістю
V0
= 2 м/с. У певний момент часу курсант
стрибає з човна зі швидкістю
= 5 м/с відносно човна під кутом
= 60° до горизонту (рис. 6). Знайти кінцеву
швидкість човна. Силами тертя нехтувати.
Розв’язок.
Перш за все, виберемо систему відліку,
зв’язавши її з яким-небудь нерухомим
об’єктом (деревом на березі) та спрямуємо
вісь
вздовж напряму руху човна. Оскільки ми
нехтуємо силами тертя, то вздовж напряму
руху зовнішні сили відсутні і ми можемо
скористуватись теоремою про збереження
компоненти імпульсу
,
де
та
початковий та кінцевий імпульси системи
відповідно. Оскільки в початковий момент
курсант знаходяться у стані спокою
відносно човна то початковий імпульс
можна записати як
.
Вертикальна
складова імпульсу курсанта зумовлює
додаткове занурення човна, яке в даному
випадку нас не цікавить. Щоб записати
-
компоненту кінцевого імпульсу системи,
який вона набуває в момент відштовхування
курсанта від човна, будемо вважати, що
напрям руху човна не змінюється, а його
швидкість дорівнює
.
Тоді компонента абсолютної швидкості
курсанта вздовж осі
буде
,
тому
.
Прирівнюючи кінцевий та початковий імпульси, отримаємо
=
,
що дозволяє визначити кінцеву швидкість човна
.
Підставимо умови задачі в отриманий вираз та знайдемо
= 2,9 (м/с).
Відповідь:
= 2,9 м/с.
Проаналізуйте
самостійно кінцеву формулу для випадків:
а)
=0°;
б)
= 90°.
П
риклад
2.
По порому
=3т,
який пливе зі швидкістю
=6
м/с рухається автомобіль масою
=
1,5 т зі швидкістю
=
2 м/с відносно порому (рис. 7). Автомобіль
починає гальмувати. Знайти швидкість
порому на момент, коли відносна швидкість
автомобілю становить
=
0,5 м/с. Опором повітря та води нехтувати.
Розв’язок. Як і у попередньому прикладі, виберемо систему відліку, зв’язавши її з яким-небудь нерухомим об’єктом (маяком на березі) та спрямуємо вісь вздовж напряму руху порому. Оскільки ми нехтуємо силами тертя, то вздовж напряму руху зовнішні сили відсутні і ми можемо скористуватись теоремою про збереження імпульсу
,
де
та
початковий та кінцевий імпульси системи
відповідно. Оскільки в початковий момент
автомобіль рухається в напрямі руху
порому, його абсолютна швидкість дорівнює
і початковий імпульс системи відносно
обраної системи відліку можна записати
як
.
Щоб
записати кінцевий імпульс системи,
будьмо вважати, що напрям руху порому
не змінюється, а його швидкість дорівнює
.
Тоді абсолютна швидкість автомобіля
вздовж осі
буде
,
і кінцевий імпульс системи відносно
нерухомої системи відліку
.
Прирівнюючи кінцевий та початковий імпульси, отримаємо
=
,
що дозволяє визначити кінцеву швидкість порома
.
Підставимо умови задачі та знайдемо
= 6,5 (м/с).
Відповідь:
= 6,5 м/с.