В) Змушені коливання з одним ступенем свободи

Якщо на матеріальну точку масою , крім квазіупружної сили та сили в’язкого тертя , діє збуджуюча (зовнішня) сила, яка змінюється за гармонічним законом

, (1)

(де – амплітуда збуджуючої сили, – її частота), то рух, який буде здійснювати точка, називається вимушеним коливаннями.

Складемо одномірне диференціальне рівняння руху такого тіла масою

, (2)

де , а і такі ж самі, як і раніше.

Розв’язок неоднорідного диференціального рівняння (2), як відомо з теорії диференціальних рівнянь, має вигляд

, (3)

де – загальний розв’язок однорідного рівняння (2) нам вже відомий (дивись формулу (8 ) параграфа „Вільні згасаючі коливання”)

, (4)

а – будь-який частковий розв’язок неоднорідного рівняння (2).

З плином часу амплітуда руху, зумовленого вільними коливаннями при наявності сил тертя, згідно (4) зменшується практично до нуля, і рух тіла буде визначатися лише зовнішньою силою (1). Час установлення режиму вимушених коливань визначається величиною коефіцієнта затухання і через проміжок часу можна розглядати лише усталені вимушені коливання для яких початкові умови вже не мають ніякого значення.

Отож, частковий розв’язок рівняння (2) знаходять у вигляді

, (5)

де сталі та отримують після підстановки функції (5) та її похідних в рівняння (1) та певних алгебраїчних перетворень:

, (6)

. (7)

Таким чином, фаза і амплітуда змушених коливань при наявності тертя визначаються як властивостями зовнішньої сили (частотою та її амплітудою), так і характеристиками осцилятора (його масою , жорсткістю та коефіцієнтом затухання ) і не залежать від початкових умов.

Крива, яка описує залежність амплітуди вимушених коливань від частоти зовнішньої сили називається амплітудно-частотною характеристикою.

Аналізувати таку криву зручно в безрозмірних частоті та параметрі затухання .

Тоді з формули (6) отримуємо

, (8)

де - статичне зміщення під дією амплітудного значення збуджуючої сили.

Максимальна величина амплітуди відповідає так званій резонансній частоті (і, відповідно, ) яка може бути знайдена з умови мінімуму знаменника формули (6)

, (9)

чи, відповідно, (8)

,

де - власна частота коливань системи при наявності сил тертя.

Підставляючи отримані вирази в (6) чи (8), отримаємо вираз для амплітуди при резонансі

. (10)

Контрольні запитання

1. Сформулюйте умови виникнення змушених коливань.

2. Запишіть диференціальне рівняння змушених коливань. Що необхідно знати для однозначного розв’язку такого рівняння?

3. Як отримати розв’язок такого рівняння?

4. Запишіть розв’язок диференціального рівняння змушених коливань.

5. Чим визначаються період змушених коливань?

6. Як впливають початкові умови на змушені коливання?

7. Як впливає сила тертя на змушені коливання?

8. За яким законом змінюється амплітуда змушених коливань? Від яких факторів залежить амплітуда змушених коливань?

9. Намалюйте графік залежності амплітуди змушених коливань від частоти збуджуючої сили для різних значень сили тертя (коефіцієнта затухання).

10. Який випадок змушених коливань називається резонансом?

П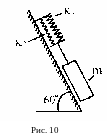 риклад. Тіло масою = 0,5 кг закріплено до двох пружин жорсткістю = 60 Н/м і = 140 Н/м на похилої площині під кутом 60° до горизонту (рис. 10) і здійснює коливання під дією зовнішньої сили при наявності сили опору Н.

1) Записати диференціальне рівняння змушених коливань та знайти значення резонансної частоти, статичне зміщення, та амплітуди змушених коливань при резонансі.

2) Побудувати амплітудно-резонансні криві в безрозмірних частотах в інтервалі (0; 2,0) для амплітуди (чи відносної амплітуди ).

Розв’язок.

Як і раніше, перш за все, знайдемо ефективний коефіцієнт жорсткості двох пружин. Зараз пружини закріплені паралельно, тому = 200 (Н/м). Запишемо диференціальне рівняння вимушених коливань с урахуванням сил тертя

,

та визначимо сталі, які входять до цього рівняння. Так:

= 20 (рад/с),

= 2/(2·0,5) = 2 (рад/с),

= 14/0,5 = 28 (м/с²).

Всі ці величини є необхідними для подальших розрахунків. Так, резонансну частоту коливань визначимо з формули (9)

= = 19,8 (рад/с),

амплітуду коливань в резонансі підрахуємо, користуючись (10):

= 0,352 (м),

а статичне зміщення – за формулою

= 28/400 = 0,07 (м).

Для побудови амплітудно-резонансних кривих в безрозмірних частотах скористуємось виразом (8)

,

або для безрозмірної амплітуди

.

Складемо таблиці значень та (Реально така таблиця будується за допомогою ПЕОМ з кроком по не менш ніж 0,01 в інтервалі 0,9 – 1,1 і кроком 0,1 за межами цього інтервалу).

	0,00	0,20	0,40	0,60	0,70	0,80	0,90	0,91	0,92	0,93
	0,070	0,073	0,083	0,108	0,132	0,178	0,267	0,280	0,292	0,304
	1,000	1,041	1,185	1,536	1,891	2,538	3,821	3,994	4,172	4,350

	0,94	0,95	0,96	0,97	0,98	0,99	1,00	1,01	1,02	1,030	1,040
	0,317	0,328	0,338	0,345	0,350	0,352	0,350	0,345	0,337	0,326	0,313
	4,522	4,683	4,822	4,931	5,001	5,025	5,000	4,926	4,809	4,655	4,476

	1,050	1,100	1,200	1,300	1,400	1,500	1,600	1,700	1,800	1,900	2,000
	0,300	0,230	0,140	0,095	0,070	0,054	0,044	0,036	0,031	0,027	0,023
	4,279	3,288	1,995	1,356	1,000	0,778	0,628	0,521	0,441	0,379	0,330

Після цього побудуємо амплітудно-резонансну криву (рис. 11).