4.4 Зоны интереса на бернуллиевских сценах
Очевидно, что все сказанное в 4.2 верно и для бернуллиевских сцен.
По определению, пиксели бернуллиевских сцен являются независимыми в совокупности случайными величинами. Этим свойством можно воспользоваться для построения методов классификации квадратов, основанных на теории проверки статистических гипотез.
Пусть
- пятно с диаметром
,
средним значением
и дисперсией
,
- семейство квадратов, определенное для
изложенным в 4.1
способом и
- квадрат из
.
Предположим (гипотеза), что случайные
величины, образующие семейство
,
имеют одно и то же распределение
вероятностей со средним значением
и дисперсией
.
Это означает, что
не является зоной интереса. Из определения
бернуллиевской сцены следует, что
изображения границы
и зоны интереса без границы
являются реализациями случайных выборок.
Поэтому на основании центральной
предельной теоремы выборочные средние
и
,
а также
их разность
-
являются
асимптотически нормальными случайными
величинами с параметрами
и
,
и
,
и
.
Выберем
в качестве
положительное число достаточно близкое
к нулю (например, 0.05, 0.01 или еще меньше)
и найдем
из уравнения
.
Для этого заменим - нормированной случайной величиной
,
и воспользуемся интегралом вероятностей
.
Он позволяет записать уравнение в виде
2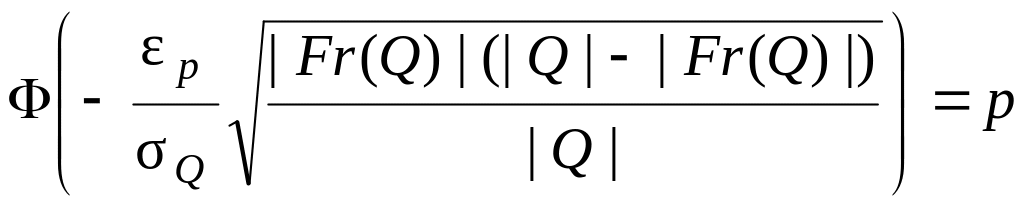
.
Таким
образом, для вычисления границ -
и
критической области
остается воспользоваться таблицей
интеграла вероятностей.
Очевидно,
что при верной гипотезе событие
является маловероятным. Это позволяет
сформулировать решающее правило для
классификации квадратов
из
в следующем виде. Если для
выполняется неравенство
,
то
не является зоной интереса. В противном
случае, когда
,
квадрат
является зоной интереса для
.
Очевидно, что вероятность правильной
классификации квадрата без объекта
равняется
,
а вероятность обнаружения ложной зоны
интереса -
.
Заметим,
что для вычисления
необходима дисперсия
.
Если она неизвестна, то можно воспользоваться
ее оценкой
или ее несмещенным
вариантом
,
которые определяются равенствами
и
,
используя
в качестве реализации выборки изображение
всей зоны.
В
качестве примера на рисунке 4.3 приведено
одно из изображений фрагмента
бернуллиевской сцены размером 511 на 511
масштабных единиц. Фрагмент содержит
19 объектов прямоугольной формы со
сторонами 29 и 14 масштабных единиц,
расположенных на тех же местах и с той
же ориентацией, что и на фрагменте,
изображения который представлен на
рисунке 4.1. Однако пиксели сцены (объектов
и фона) имеют равномерное распределение
со средними значениями
и
соответственно, одной и той же дисперсией
.
Поэтому
.
При радиусе сглаживания
относительная частота количества
объектов, для которых удалось построить
зоны интереса по этому изображению,
составила 0.53.
|
Рисунок 4.4 - Изображение фрагмента бернуллиевской сцены ( ) |
|
