3.3. Ввод исходных данных

Исходными данными для расчета являются диаметр исходной заготовки и, если заготовка будет штамповаться из листа его размеры.

Лабораторная работа № 4

2. Оптимальный раскрой полос или штучных заготовок

2.1. Постановка задачи

Однорядная штамповка деталей из ленты (полосы) определяется двумя параметрами: шириной половы b и шагом штамповки h (рис. 2.1.).

Коэффициент использования металла  определяется для штамповки из полосы длиной l как отношение площади S_д n деталей, полученных из полосы, к площади полосы S_п (см. рис. 2.1.).

.

Рис. 2.1. Раскрой полосы на заготовки

При штамповке из ленты, когда длина ленты велика, концевые отходы можно не учитывать и коэффициент использования металла определяется как

.

Рис. 2.2. Раскрой штучной заготовки

Под оптимальным раскроем в данном случае понимается нахождение таких величин h и b или a и b, при которых значение  максимально.

2.2. Математическое обеспечение

2.2.1. Кодирование контура заготовки

Для решения задачи оптимизации раскроя необходимо каким-либо образом описать контур исходной заготовки. В общем случае контур любой детали (заготовки) может быть представлен как произвольное сочетание прямоугольных и криволинейных элементов (рис. 2.3.)

Криволинейные элементы могут быть представлены как совокупность дуг окружностей с различными радиусами.

Для того чтобы описать заготовку, необходимо на её контуре найти узловые точки, то есть такие точки, в которых происходит смена линии, ограничивающей контур заготовки. Если координаты всех узловых точек, а также координаты центров кривизны дуг окружности известны, то описание контура можно задать перечислением в определённом порядке координат узловых точек и кодом характера линий между ними (см. рис. 2.3.)

2.2.2. Определение площади заготовки

Для вычисления КИМ необходимо знать площадь заготовки. Так как фигура заготовки представлена в виде отрезков прямых и дуг окружности, то для определения площади фигуры её можно представить состоящей из площади многоугольника, к которой прибавляются (в случае выпуклой дуги) или отнимаются (в случае вогнутой дуги) площади сегментов (рис. 2.4.)

Рис. 2.3. Контур исходной заготовки

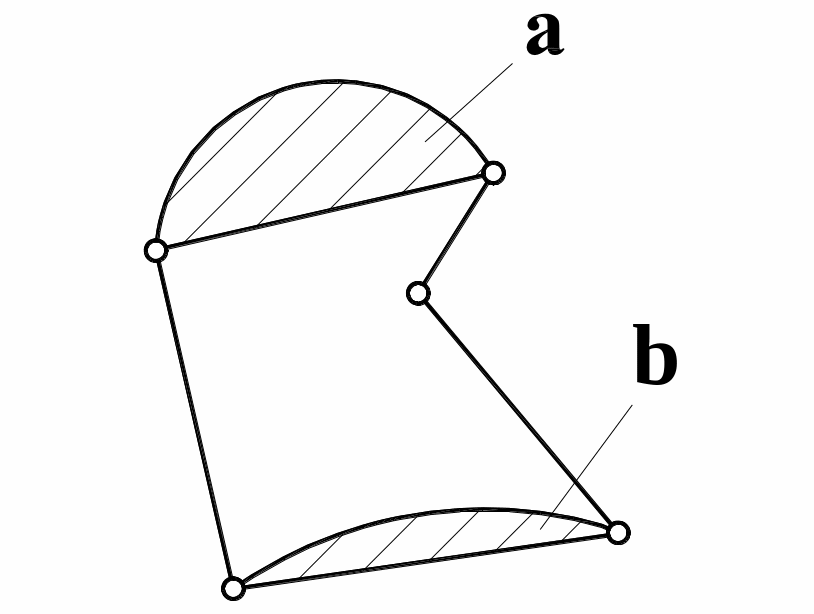
Рис. 2.4. Определение площади фигуры

а – площадь прибавляется;

b – площадь отнимается

Площадь многоугольника определяется по формуле

,

где - координаты i-той точки;

- координаты i-той–1 точки

Для определения площади сегмента, находящегося между i-1 и i-той узловой точкой, вычислим величину радиуса дуги окружности:

,

где х_цi, у_цi – координаты центра дуги.

Расстояние от i до i-1 точки найдём как

,

вычислим вспомогательную величину

.

Найдём величину центрального угла

.

Площадь сегмента вычисляется следующим образом:

,

где знак плюс ставится для выпуклой дуги, минус для вогнутой дуги.

Площадь заготовки определяется как

,

где - сумма площадей сегментов.

2.2.3. Определение оптимального размера штучной заготовки

При вырубке детали из штучной заготовки контур детали должен целиком находиться внутри штучной заготовки (см. рис. 2.2.). Геометрически это означает, что вокруг контура заготовки описан прямоугольник. Если принять, что контур заготовки параллелен осям ОХ и ОУ, а деталь может занимать произвольное положение на плоскости, то каждому произвольному положению детали будет соответствовать заготовка с различными размерами.

Пусть имеется деталь, заданная координатами узловых точек. Размер описанного прямоугольника будет зависеть от угла поворота _i детали относительно начального положения (рис. 2.5.)

Рис. 2.5. Исходная (I) и повёрнутая (II) деталь в штучной заготовке

Поворачивая контур детали на дискретный угол, получаем каждый раз новое значение:

а_i – ширины описанного прямоугольника;

b_i – длины описанного прямоугольника.

Площадь описанного прямоугольника составляет

.

Коэффициент использования металла определяется по формуле

.

Из полученных значений находим максимальное , соответствующие ему значения и дадут размер оптимальной штучной заготовки.

Фигура задана массивом координат узловых точек, центров окружностей и кодами видов линий между узловыми точками. Так как работа с криволинейным контуром усложняет программу и удлиняет время расчёта, то предлагается прямые линии аппроксимировать отрезками прямых. Для этого создана специальная подпрограмма. Подпрограмма аппроксимации преобразует заданную информацию о контуре заготовки в массив координат узловых точек, между которыми находятся только отрезки прямых линий.

Расчёт проводим в следующей последовательности.

Фигура задана массивом координат узловых точек

х 1,	х2,	х3,	…,	х n
y1,	y2,	y3,	…,	yn

При повороте фигуры на дискретный угол _I образуется новый массив точек

х 1,	х2,	х3,	…,	х n
y1,	y2,	y3,	…,	yn

где х_i и y_i определяется как

Для определения размера заготовки необходимо найти точки с минимальными и максимальными значениями координат , . По этим значениям находятся размеры заготовки:

По формуле (2.3) определяем коэффициент использования металла.

Такой расчёт проводим для углов с определённым шагом (например, через 1) и получаем множество значений для каждого угла поворота . Из полученного множества значений находим максимальное . Соответствующие этому значению КИМ величины и являются исходными для определения величины заготовки. Для определения фактических размеров заготовки необходимо учесть величину боковых кромок или штамповочных перемычек а и b: