20

Лабораторная работа № 1

Оптимальный раскрой листов на штучные заготовки или полосы

1.1. Постановка задачи

Оптимизацию раскроя листов на штучные заготовки или полосы наиболее целесообразно проводить для оптимальных размеров штучных заготовок или полос, рассчитанных о помощью ЭВМ. Эффективность раскроя определяется коэффициентом использования металла:

(1.1)

где - площадь всех заготовок, получаемых из листа;

- площадь листа;

- число заготовок из листа;

- площадь одной заготовки;

А, В - размеры листа.

Задача оптимального раскроя листов может быть сведена к трем частным случаям:

1. Имеются листы одного габарита, определенного ГОСТом. Даны размеры и количество заготовок. Требуется определить раскрой, дающий минимальное количество отходов.

Такая проблема возникает чаще всего в мелкосерийном производстве при заказе листов одного типоразмера, что диктуется условиями поставки материала.

2. Имеются листы нескольких габаритов, определенных ГОСТом. Даны размеры и количество заготовок. Требуется определить раскрой, имеющий минимальное количество отходов.

Эта задача возникает в крупносерийном и массовом производстве, когда для некоторых крупногабаритных заготовок целесообразнее заказ листов другого габарита.

3. Имеются листы нескольких габаритов, в том числе и нестандартных, и известно количество листов данного типоразмера. Даны размеры и количество заготовок. Требуется определить раскрой, имеющий минимальное количество отходов.

Эта задача возникает при использовании крупногабаритных отходов, образующихся при штамповке других деталей.

Таким образом, весьма широкий круг практических вопросов раскроя можно свести к трем типам задач.

Практически наиболее часто встречается задача оптимального раскроя листов на одинаковые прямоугольные заготовки или полосы.

1.2. Технологические ограничения

Задача оптимизации раскроя ласта решается при следующих ограничениях технологического характера:

- условие «гильотинного» реза, т.е. лист или остаток листа режется целиком от края до края;

- учет минимального остатка под прижим (рис. 1.1);

- максимальная длина реза на должна превышать возможной для конкретного вида оборудования;

- форма и величина отхода должны позволять использование его для штамповки более мелких деталей.

Рис. 1.1. Определение величины минимального остатка под прижим:

1 - верхний нож; 2 - нижний нож; 3 - прижим; 4 - заготовка; 5 - защитное ограждение; - величина минимального остатка под прижим

Учет этиx ограничений позволяет успешно реализовать оптимальную схему раскроя на имеющемся оборудовании.

1.3. Математическое обеспечение

Наиболее распространенной является простая схема раскроя (рис.4.2).

Для определения схемы раскроя рассмотрим лист размером А х В, где А - ширина листа, В - длина листа.

Заготовки на листе располагаются либо широкой стороной вдоль узкой стороны листа, либо широкой стороной вдоль широкой стороны листа. Для нахождения наилучшей схемы раскроя необходимо рассмотреть оба варианта.

При резке листа размером А х В на заготовки размером а х в образуются полосы размером А х в и отход размером А х h_в. Количество полос равно

, (1.2)

где - целая часть числа.

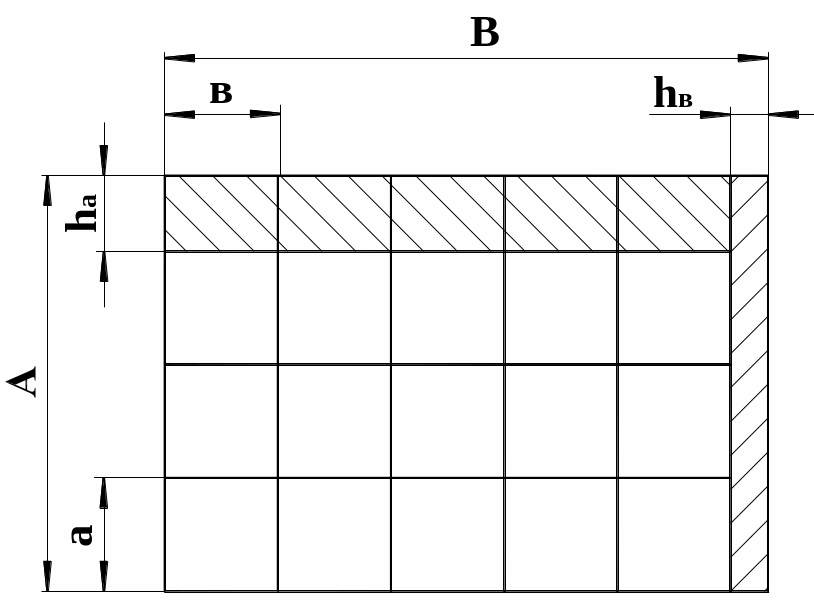
Рис. 1.2. Простой раскрой листа на одинаковые прямоугольные заготовки

Ширина отхода h_в равна

. (1.3)

Если величина h_в больше минимального остатка под прижим , то расчёт закончен.

Если h_в < , то величина остатка недостаточна. В этом случае последняя полоса остается вместе с отходом и, как правило, идет на штамповку другой детали.

Количество полос, получаемых из листа, в этом случае равно

. (1.4)

Размер последней полосы h^’_в определяется так:

. (1.5)

Количество заготовок из полосы определяется следующим образом:

. (6)

Величина отхода от полосы равна

. (1.7)

Полученную величину необходимо сравнить с остатком под прижим .

Если , то расчет закончен. Если , то последняя заготовка не режется и остается вместе с отходом. В этом случае количество заготовок равно

. (1.8)

Величина отхода равна

. (1.9)

Обще количество заготовок из листа равно

. (1.10)

Заменяв в формулах (2 - 10) значение а на значение в и наоборот, получим второй вариант раскроя. Из двух вариантов можно выбрать наилучший.

Комбинированный раскрой листа на одинаковые прямоугольные заготовки

Простой раскрой, как правило, редко дает высокий выход годного. Для повышения эффективности использования металла необходимо применять более сложные схемы раскроя, можно, например, от листа отрезать несколько полос определенной ширины, затем повернуть остаток листа на 90 градусов и продолжать резать на полосы той же ширины. Перебором всех вариантов соотношений между количеством заготовок, например из целой части листа, и количеством заготовок, получаемых из повернутого остатка можно найти такой вариант, при котором общее количество заготовок, полученных из листа, будет максимальным.

Рассмотрим раскрой листа размером А х В, из которого надо получить заготовки размером а х в

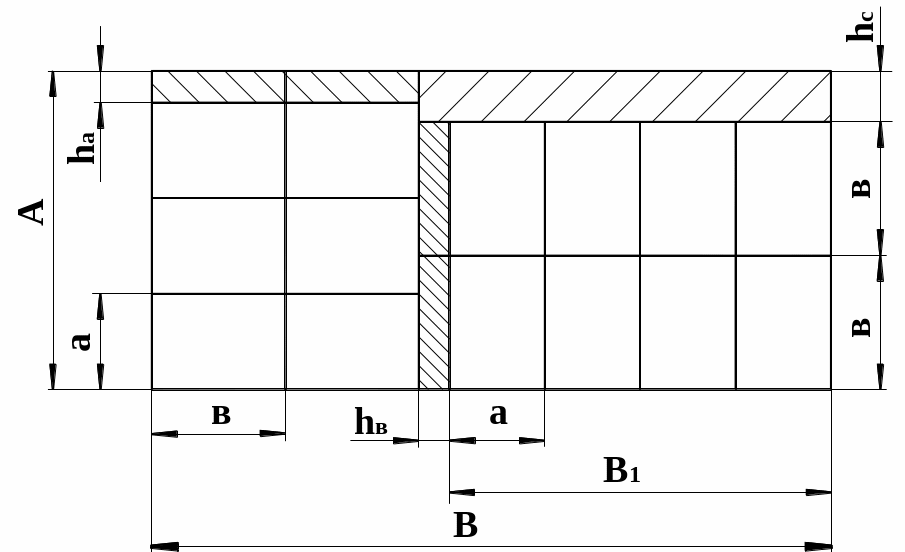
Рис. 4.3. Комбинированный раскрой листа на одинаковые прямоугольные заготовки

По формулам (1.2. - 1.6) необходимо определить количество заготовок, целиком вмещающихся какой-либо одной стороной (например, с длиной в) вдоль длинной ( ) и вдоль короткой ( ) сторон листа.

Отрем от листа i полос размером А х в (i = 1, 2, … ) (см.рис 1.3), причём заготовки расположены длинной стороной вдоль длинной стороны листа. Из каждой полосы получается деталей:

Из этих i полос получается N₁ деталей:

Оставшаяся часть листа имеет размеры A х В₁, где

В этой части листа заготовки расположены длинной стороной вдоль короткой стороны листа А. В результате можно получить полос размером а х А :

.

Из каждой полосы получается заготовок:

.

Таким образом, из оставшейся части листа получается заготовок:

Общее количество заготовок, получаемых из листа по этой схеме раскроя, равно

(1.16)

Так как N₁ и N₂ зависят от i то и N также зависит от i. Перебором i =1, 2, … можно найти N_max Соответствующее этому значению i покажет оптимальную схему раскроя. Ограничения на величину учитываются аналогично простому раскрою.

1.4. Ввод исходных данных

Исходными данными для расчёта являются:

- размеры листа;

- размеры заготовки;

- величина минимального остатка на прижим.

Результаты расчёта простого раскроя:

- выбор варианта раскроя;

- количество полос из листа;

- количество заготовок из полосы;

- количество заготовок получаемых из листа;

- размеры отхода.

Результаты расчёта комбинированного раскроя:

- выбор варианта раскроя;

- количество полос из листа (N₁);

- количество полос из листа (N₂);

- количество заготовок из полосы ( );

- количество заготовок из полосы ( );

- количество заготовок получаемых из листа;

- размеры отхода.