10. Третий закон термодинамики. Теорема Нернста

Феноменологическое определение энтропии позволяет найти в обратимом процессе лишь ее изменение, а не абсолютную величину. Последнюю можно найти на основе третьего закона термодинамики.

На основе опытных данных Нернст (1906) сформулировал гипотезу, получившую название теоремы Нернста: «При всех изменениях, происходящих в чистых веществах при абсолютном нуле, изменение энтропии равно нулю». Таким образом

. (10.1)

Планк предложил энтропию тела при абсолютном нуле принять равной нулю:

. (10.2)

Теорема Нернста не следует из первого и второго законов термодинамики, а связана с третьим законом термодинамики, которая гласит, что никакую систему невозможно охладить до абсолютного нуля.

Рассмотрим систему, охлаждаемую от температуры T₁ до T₂ путем изменения внешнего параметра  (например, объема V или магнитного поля ). Температура окружающих тел выше, поэтому для достижения самых низких температур процесс должен быть адиабатическим, т.е. энергия системы должна уменьшаться за счет совершения ею работы. Охлаждение будет наиболее эффективным, если процесс является обратимым, так как в обратимом адиабатическом процессе работа максимальна ( ). Для адиабатического процесса

. (10.3)

Допустим, что достигли T₂ = 0. Тогда, используя разложение

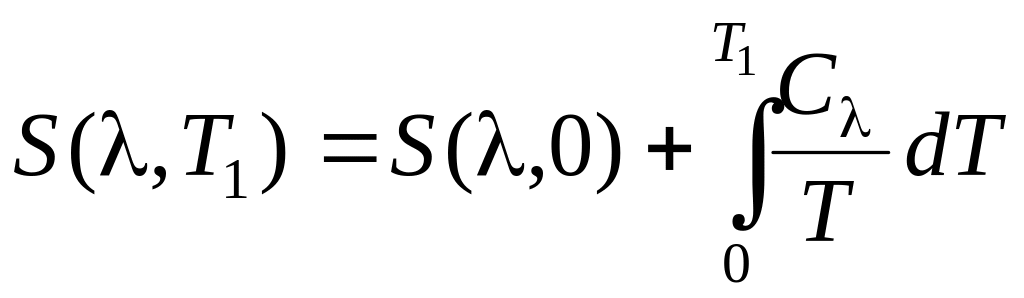, (10.4)

где – теплоемкость системы при  = const, можем записать

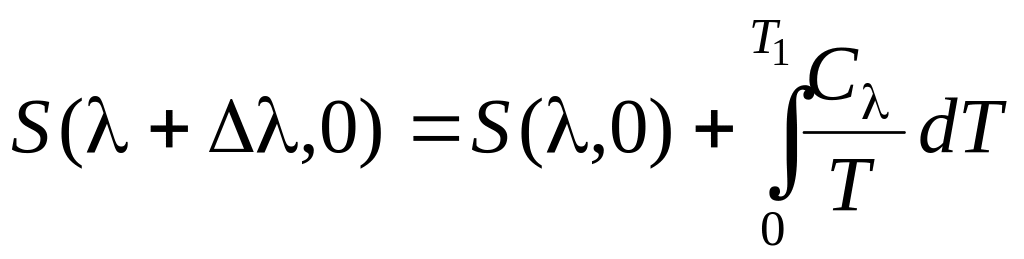. (10.5)

Теплоемкость C_ положительна, поэтому при T = 0 получаем

. (10.6)

Но, поскольку, согласно третьему закону термодинамики невозможно от температуры T₁ > 0 охладить систему до T₂ = 0, можно заключить, что

при T = 0. (10.7)

Это утверждение совпадает с теоремой Нернста (1).

Из формулы (5) при условии (7) получаем

при T  0, (10.8)

откуда следует, что теплоемкость C_ системы стремится к нулю при T  0.

11. Фаза. Равновесие между фазами чистого вещества

Под фазой понимают термодинамически однородную часть неоднородной системы. Например, пар и вода могут рассматриваться как две фазы одного вещества (компонента), если они являются частями одной системы.

Обычно фазы разделены поверхностью, при переходе через которую физические свойства вещества изменяются скачкообразно. Вещество в определенной фазе может состоять из пространственно разделенных частей и относиться к одной и той же фазе. Например, капельки жидкости, образующие туман, относятся к жидкой фазе, хотя поверхность, отделяющая их от газа, не является единой.

Следует обратить внимание на то, что термодинамическое понятие фазы шире, чем понятие агрегатного состояния вещества. Например, кристаллы различных модификаций относятся к различным фазам, но к одному и тому же агрегатному состоянию. Сюда же можно отнести примеры ферромагнитной и парамагнитной фаз и многие другие. Стоит отметить, что в современной физике, особенно при изучении сложных систем, понятие фазы трактуется еще шире. Например, когерентное излучение лазера может рассматриваться как новая фаза по отношению к некогерентному излучению накачки (Г.Хакен), состояние тонкой магнитной пленки с полосовой магнитной структурой и состояние со структурой цилиндрических магнитных доменов также могут рассматриваться как разные фазы.

В зависимости от условий возможно сосуществование фаз без изменения их масс. В этом случае говорят о фазовом равновесии.

Рассмотрим изолированную систему, состоящую из двух внутренне равновесных подсистем, которые представляют собой две фазы одного и того же вещества. Для этой системы имеют место условия:

U = U₁ + U₂ = const, V = V₁ + V₂ = const, N = N₁ + N₂ = const. (11.1)

В силу условий (1) изменения параметров подсистем связаны соотношениями:

dU₁ = – dU₂, dV₁ = – dV₂, dN₁ = – dN₂. (11.2)

Когда подсистемы придут в равновесие между собой, энтропия системы достигнет максимума. Поэтому будет иметь место соотношение

. (11.3)

Подставив сюда выражения:

, (11.4)

, (11.5)

и учитывая (2), получаем

. (11.6)

Так как приращения dU₁, dV₁ и dN₁ произвольны, условие равновесия подсистем имеют вид:

T₁ = T₂; P₁ = P₂; ₁ = ₂. (11.7)

Здесь первое равенство отвечает тепловому равновесию подсистем, второе – механическому, а третье – материальному или диффузионному равновесию.

Условия равновесия (7) для двух фаз одного вещества можно записать в виде функционального равенства

₁(P,T) = ₂(P,T). (11.8)