5. Теплоемкость. Уравнение состояния. Замена независимых переменных

Теплоемкость C системы равна количеству теплоты, которое надо подвести при заданных условиях к системе, чтобы повысить ее температуру на единицу (обычно на 1 К):

. (5.1)

Вводят также удельную (массовую) теплоемкость c = C/m и молярную C_ = C/m теплоемкости, где m – масса тела,  – молярная масса вещества.

Так как теплота – функция процесса, теплоемкость зависит от конкретного вида процесса. Наибольший практический интерес вызывают теплоемкость при постоянном объеме

(5.2)

и при постоянном давлении

. (5.3)

Обычно в эксперименте измеряют C_P, тогда как теоретически удобнее рассчитывать C_V. Поэтому важно установить между ними связь. Если внутренняя энергия задана как функция U(V,T), то эта связь устанавливается соотношением

, (5.4)

доказать которое рекомендуется в качестве упражнения. Для идеального газа , , и из уравнения (4) получаем известное соотношение Майера: .

Величины в правой части формулы (4) могут быть связаны с экспериментально определяемыми величинами: коэффициентом теплового расширения и изотермической сжимаемостью вещества .

Эта связь имеет вид

. (5.5)

Уравнение состояния. Равновесные состояния термодинамической системы полностью характеризуются некоторым относительно небольшим набором независимых термодинамических параметров, например, давлением p, объемом V, температурой T, намагниченностью , поляризацией вещества и т.п. Существующая между термодинамическими параметрами конкретной системы связь устанавливается уравнением состояния. К таким уравнениям относятся, например:

• pV = constT – уравнение состояния идеального газа;

• (p + a/v²)(v – b) = constT – уравнение Ван дер Ваальса,

где a, b – постоянные, v – удельный объем.

Для каждой конкретной системы уравнения состояния определяются эмпирически или методами статистической механики, так что в рамках термодинамики они считаются заданными при определении системы.

Замена независимых переменных. Иногда в термодинамике в качестве независимых переменных рассматриваются p и V, а иногда T и V. Поэтому в записи частных производных необходимы индексы, указывающие на то, какие переменные сохраняются постоянными, например или .

Для замены независимых переменных удобно пользоваться тождеством

(5.6)

или

. (5.7)

Эти соотношения легко получить из равенства

. (5.8)

Если z = const, то dz = 0 и отношение dx/dy =  должно иметь вид (7).

6. Применение первого закона термодинамики к простым системам. Идеальный газ, изопроцессы

Идеальный газ – модель реального газа, которая удовлетворяет следующим требованиям:

• расстояние между молекулами гораздо больше их размеров (молекулы можно считать материальными точками);

• силами взаимодействия, кроме моментов соударения, можно пренебречь (потенциальная энергия взаимодействия молекул по сравнению с кинетической энергией хаотического движения пренебрежимо мала);

• столкновение молекул друг с другом и со стенками абсолютно упругое;

• движение каждой молекулы подчиняется классическим законам динамики.

• реальный разреженный газ приблизительно ведет себя как идеальный газ.

Изопроцессы – равновесные процессы, в которых один из основных параметров сохраняется.

Изобарный процесс ( ) Для изобарного процесса в идеальном газе справедлив закон Гей-Люссака: при постоянном давлении объем данной массы газа прямо пропорционален его термодинамической температуре:

 или .

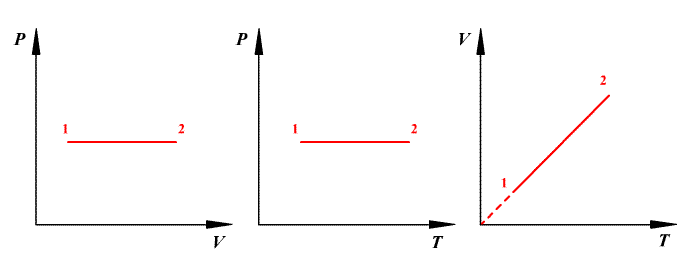
Работа газа при изобарном расширении:

.

Изменение внутренней энергии:

Количество полученного тепла:

.

Молярная теплоемкость при изобарном процессе:

.

Изохорный процесс ( ) Изохорный процесс в идеальном газе описывается законом Шарля: при постоянном объеме давление данной массы газа прямо пропорционально его термодинамической температуре:

 или .

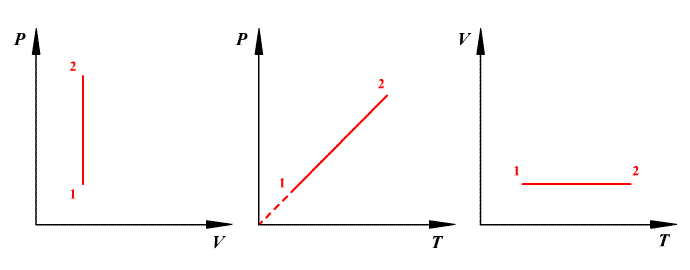
Работа газа при изохорном процессе равна нулю: .

Все полученное тепло идет на изменение внутренней энергии согласно первому закону термодинамики:

.

Молярная теплоемкость при изохорном процессе:

.

Изотермический процесс ( ) Изотермический процесс в идеальном газе подчиняется закону Бойля - Мариотта: для данной массы газа при неизменной температуре произведение значений давления и объема есть величина постоянная:

 или .

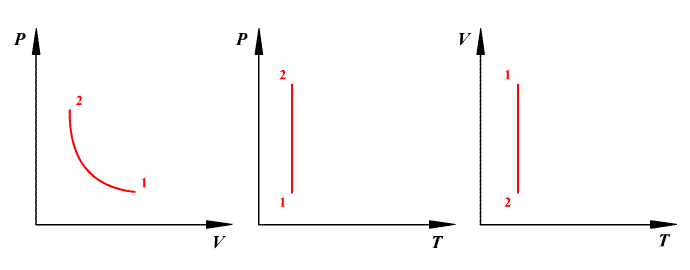
Работа газа при изотермическом расширении:

.

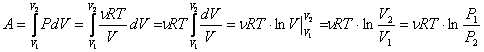Изменение внутренней энергии при изотермическом процессе равно нулю:

.

Все полученное тепло идет на совершение работы в соответствии с первым началом термодинамики:

.

Адиабатный процесс – процесс, при котором отсутствует теплообмен между системой и окружающей средой.

Из первого начала термодинамики следует, что работа газа при адиабатном процессе совершается за счет его внутренней энергии:

(6.1)

С другой стороны, из уравнения Клапейрона-Менделеева следует:

(6.2).

Разделим уравнение (2) на уравнение (1):

,

где показатель адиабаты: .

Проинтегрируем полученное уравнение:

.

Таким образом, при адиабатном процессе  или – уравнение Пуассона. С учетом уравнения Клапейрона-Менделеева ( , ) уравнение Пуассона может быть представлено в виде:

 или ;  или .

График адиабатного процесса — более крутая кривая, чем гипербола при изотермическом процессе. Это следует из выражения производной , полученной из уравнения Пуассона.

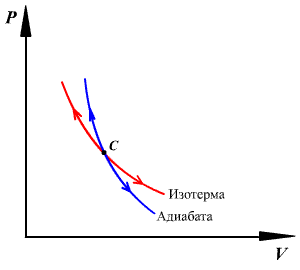
Работа газа при адиабатном процессе равна убыли внутренней энергии:

.

Политропный процесс.

Рассмотренные изобарный, изохорный, изотермический и адиабатический процессы имеют общую особенность – они происходят при постоянной теплоемкости.

В первых двух процессах теплоемкости соответственно равны С_V и С_p, в изотермическом процессе (dT = 0) теплоемкость равна ±∞, в адиабатическом (δQ = 0) теплоемкость равна нулю.

Процесс, в котором теплоемкость остается неизменной, называется политропным.

Исходя из первого начала термодинамики при условии постоянства теплоемкости (C = const) можно вывести уравнение политропы:

(6.3)

где n = (С – С_p)/(С – С_V) – показатель политропы.

При С = 0, n = γ, из (3) получается уравнение адиабаты; при С = 0, n = 1 – уравнение изотермы; при С = С_p, n = 0 – уравнение изобары, при С = С_V, n = ±∞ – уравнение изохоры. Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.

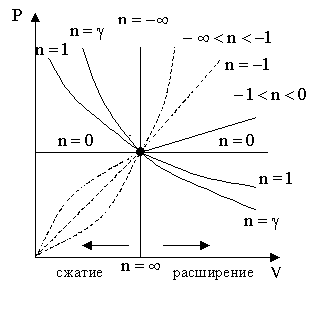
Теплота в политропном процессе: ,

где С – теплоемкость политропного процесса.

Процессы расширения

1. : (тепло подводится), .

2. : , .

3. : (тепло отводится), .

Процессы сжатия

1. : , .

2. : , .

3. : , .