4.3. Контрольные вопросы
1. Что такое полный факторный эксперимент и чем он отличается от дробного факторного эксперимента?
2. В чём заключается основное преимущество однофакторного эксперимента?
3. За счёт чего возможно уменьшение числа опытов при проведении экспериментальных исследований?
4. Что такое двухуровневый эксперимент и в чём его преимущества и недостатки по сравнению с многоуровневыми исследованиями?
5. В какой форме удобнее всего представлять результаты многофакторных исследований?
6. Что такое физическое моделирование процесса?
7. В чём заключается смысл математического моделирования?
8. Какое значение имеет экспериментальное исследование в процессе моделирования объекта?
9. Какие основные задачи решает дисперсионный анализ результатов?
10. Что является целью корреляционного анализа?
11. Что такое статистическая модель объекта?
12. В каких случаях необходимо использование планов второго порядка ?
13. Что характеризует почти стационарную область?
14. С какой целью используется критерий Стьюдента при корреляционном анализе?
15. Каково назначение критерия Фишера и что он выражает?
5. Решение задачи оптимизации технологических параметров
Во многих случаях инженерной практики перед исследователем возникает задача не только выявления характера связи между двумя или несколькими рядами наблюдений, но и нахождения таких численных значений факторов, при которых отклик (выходной параметр) достигает своего экстремального значения (максимума или минимума). Эксперимент, решающий эту задачу, называется экстремальным. В этом случае задача сводится к оптимизационной и формулируется следующим образом: требуется определить такие координаты экстремальной точки (х1*, х2*...., xк*) поверхности отклика у = f(x1, x2, ..., xк), в которой она максимальна (минимальна): уmax = f(х1*, х2*...., xк*).
Графическая интерпретация задачи оптимизации объекта у = f(х, х2) при двух факторах х, х2 представлена на рис. 5.1 (а, б).
Здесь точка А соответствует оптимальным значениям факторов х1*, и х2*, обеспечивающим максимум функции отклика уmax. Замкнутые линии на рис. 5.1(б) характеризуют линии постоянного уровня и описываются уравнением у = f(x1, х2) = В = соnst.
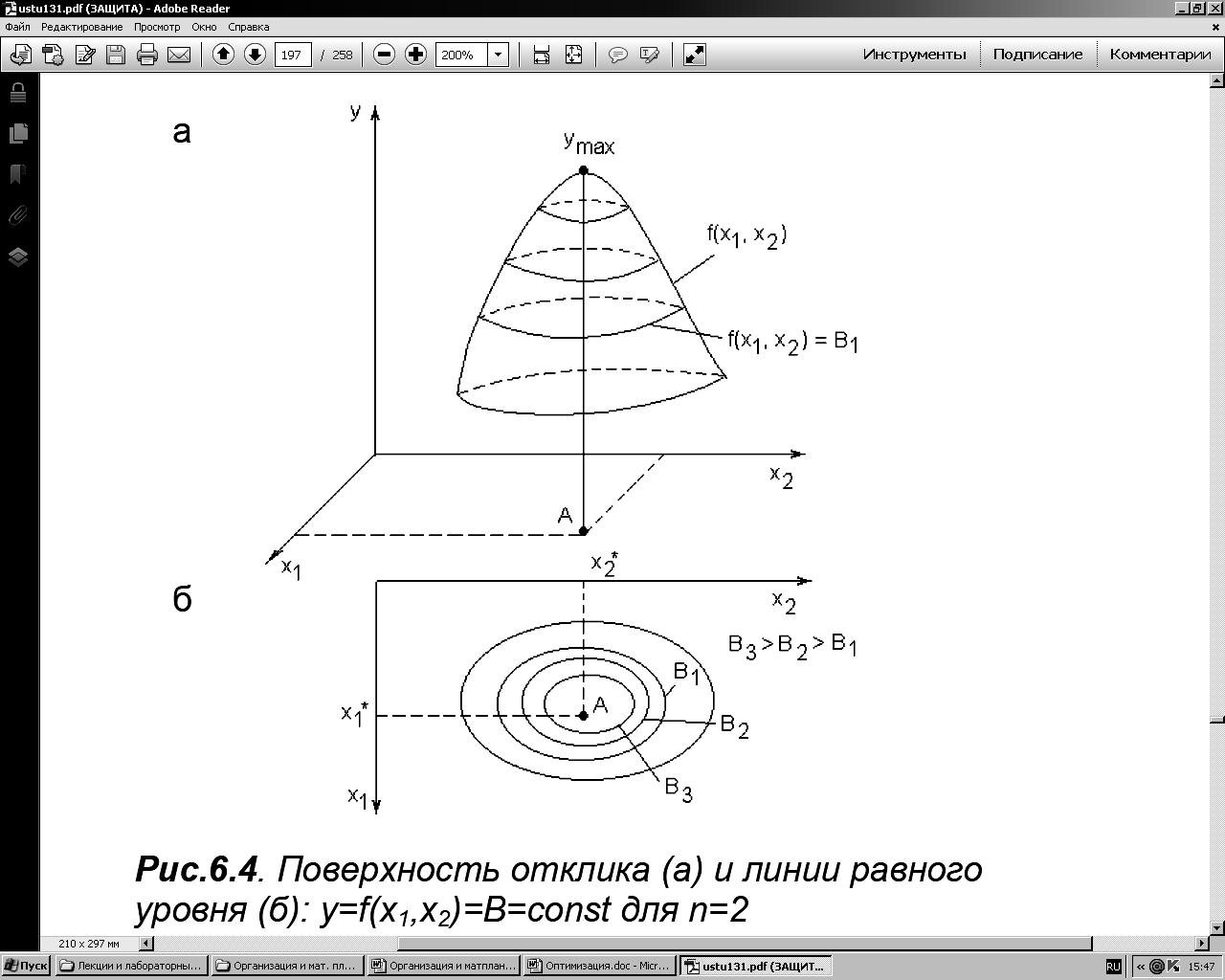
Рис. 5.1. Поверхность отклика (а) и линии равного уровня (б):
y = f(x1,x2) = B = Const для n = 2
Известный из практики метод «проб» и «ошибок», в котором факторы изменяются на основании опыта, интуиции или наугад, при значительном числе факторов зачастую оказывается малоэффективным. Поисковые методы оптимизации, где шаговое варьирование факторами производится целенаправленно по определенному плану, требуют значительно меньшего числа опытов и быстрее приводят к цели. Поисковые методы оптимизации относятся к классу итерационных процедур, при этом весь процесс разбивается на шаги. На каждом шаге ставится ряд опытов и определяется, каким образом нужно изменить факторы, влияющие на процесс, чтобы получить улучшение результата. При этом на каждом очередном шаге получаемая информация используется для выбора последующего шага.
Разработано множество методов пошаговой оптимизации, которые подробно рассматриваются в разделе вычислительной математики – «Численные методы оптимизации». Рассмотрим только некоторые из них, эффективность использования которых в промышленном и лабораторном эксперименте применительно к металлургическим процессам подтверждена практикой.