Распределение f-критерия Фишера при 5-процентном уровне значимости

f2	f1
	1	2	3	4	5
1	164,4	199,5	215,7	224,6	230,2
2	18,5	19,2	19,2	19,3	19,3
3	10,1	9,6	9,3	9,1	9,0
4	7,7	6,9	6,6	6,4	6,3
5	6,6	5,8	5,4	5,2	5,1

В области факторного пространства, в которой линейная модель становится неадекватной, доминирующим является взаимодействие факторов. Для адекватного описания этой области факторного пространства необходимо использовать нелинейные полиномы, поскольку функция отклика в этой области часто имеет экстремумы. Эту область называют обычно почти стационарной. Для описания этой области применяют обычно полиномы 2-го порядка. Это связано с тем, что поверхности 2-го порядка легко поддаются систематизации и определению экстремума.

Близость почти стационарной точки можно установить, если поставить дополнительно к факторному плану 2^k или 2^k-p опыты в центре плана (x₁=0, x₂=0,……x_k=0) и вычислить среднее значение y₀ , которое является оценкой для свободного члена уравнения регрессии. Свободный член b₀, подсчитываемый в факторном уравнении по формуле

является совместной оценкой для свободного члена и суммы квадратичных членов, т.е.

П оэтому разность

может служить мерой кривизны поверхности отклика. Если разность b₀ - y₀ превышает ошибку эксперимента и полученное уравнение регрессии неадекватно, следует применять для описания процесса полиномы 2-го порядка.

Для описания такой поверхности отклика нужно иметь систему планирования, в которой каждая переменная будет принимать хотя бы три разных значения. Трехуровневый план, в котором реализованы все возможные комбинации, представляет собой ПФЭ типа 3^k, требует слишком большого числа опытов, намного превышающего число определяемых коэффициентов. Например, в таблице приведено сопоставление числа опытов полного факторного эксперимента и число определяемых коэффициентов:

Табл. 4.4

Число опытов для ПФЭ при различном числе факторов

k	2	3	4	5	6
N	9	27	81	243	729
Число коэффициентов	6	10	15	21	28

Сократить число опытов можно, если воспользоваться так называемыми композиционными планами, предложенными Боксом и Уилсоном в 1951 году. Такое планирование получается путем добавления некоторого количества специально расположенных точек к ядру плана, образованного планированием для линейного приближения. Ядро такого плана составляет ПФЭ 2^k при k < 4 или полуреплику от него при k > 4. Возможность использования в качестве ядра плана полуреплики при k > 4 обусловлена тем, что уже полуреплика обеспечивает получение несмещенных оценок для линейных эффектов и эффектов парных взаимодействий.

Рассмотрим составление матрицы планирования 2-го порядка для случая, когда k = 2. Полный факторный эксперимент типа 2² при планировании первого порядка представляет собой четыре опыта, поставленные в вершинах квадрата (рис. 4.4)

Пятый опыт ставится в центре плана (x₁=0, x₂=0) для оценки кривизны поверхности. Если разница между значением выхода в нулевой точке и величиной коэффициента b₀ оказывается существенной и линейного приближения недостаточно, то:

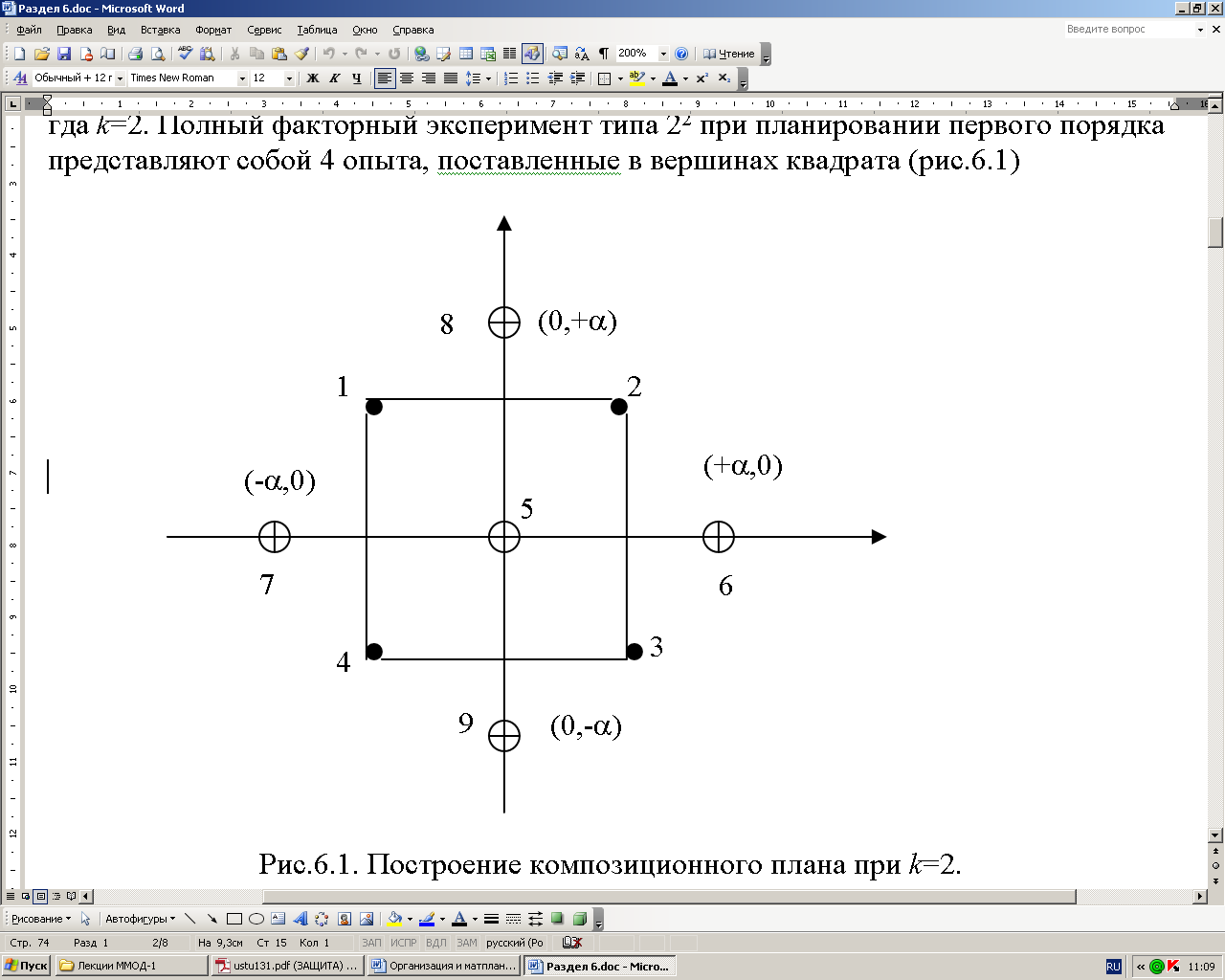
Рис. 4.4. Построение композиционного плана при k=2.

1. дополнительно ставят еще 4 опыта в так называемых звездных точках с координатами ( ), ( ), ( ), ( );

2. увеличивают, если необходимо, количество опытов в нулевой точке.

Общее число опытов при k факторах при композиционном планировании буде равно:

N = 2^k + 2k + n₀.

Такое планирование будет содержать значительно меньшее число опытов, чем ПФЭ типа 3^k. Если мы положим k = 3 и ограничимся тремя опытами в центре плана n₀ = 3, то общее число опытов будет

N = 2³ + 2∙3 + 3 = 17,

что заметно меньше, чем при использовании ПФЭ типа k³ = 3³ = 27.

Для использования планов таково вида необходимо воспользоваться специальной литературой по планированию экспериментов, рекомендованной для самостоятельной работы в составе данного лекционного курса.