4.1. Статистические методы получения математических моделей. Корреляционный анализ

При сложном и малоизученном механизме протекания процессов в технологических объектах, особенно при действии многочисленных случайных возмущений на объект, трудно сформулировать адекватное математическое описание, отражающее механизм протекающих процессов. В этом случае мы можем просто выделить выходные переменные, характеризующие состояние объекта, и входные переменные, оказывающие влияние на протекание процессов в объекте. Обозначим вектор входных переменных через:

А вектор выходных переменных через:

В общем случае можно записать функциональную зависимость между выходными и входными переменными в следующем виде:

.

Разлагая зависимость в ряд Тэйлора её можно записать в следующем виде:

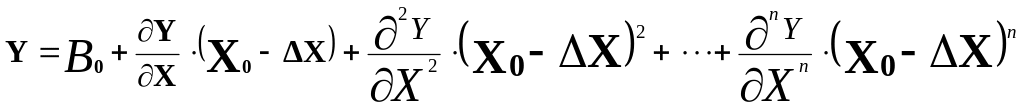
В большинстве случаев можно ограничиться разложением до вторых производных. Поэтому из этой уравнение связи в виде полинома второго, а иногда и первого порядка:

Для определения коэффициентов уравнений математической модели применяют обычно метод корреляционного анализа.

Методы корреляционного анализа широко используются для выявления зависимостей между случайными величинами по экспериментальным данным. Для экспериментального изучения зависимости между случайными величинами Х и У производят некоторое количество n независимых опытов. Результат i-го опыта дает пару значений (x_i,y_i), где i=1,2,…,n.

О наличии или отсутствии корреляции между двумя случайными величинами качественно можно судить по виду поля корреляции, нанеся точки (x_i,y_i) на координатную плоскость. Положительная корреляция между случайными величинами представлена на рис.4.1(а). Еще более тесная корреляция, близкая к линейной, представлена на рис.4.1(б). На рис. 4.1(в) приведен пример сравнительно слабой, отрицательной корреляции, а на рис. 4.1(г) – пример фактически некоррелированных случайных величин.

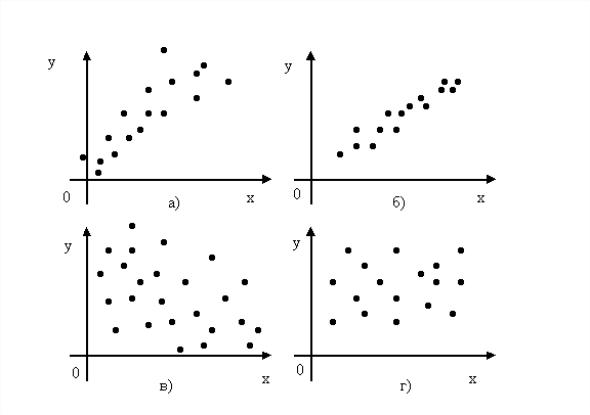Рис. 4.1. Поле корреляции случайной величины

Для количественной оценки тесноты связи служит выборочный коэффициент корреляции.

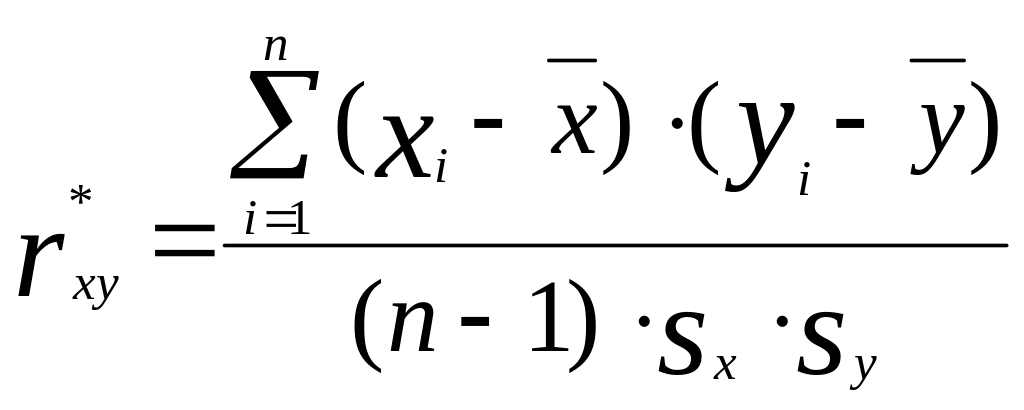
где: - среднеарифметические оценки математического ожидания величин х и у;

s_x,s_y – выборочные дисперсии величин х и у.

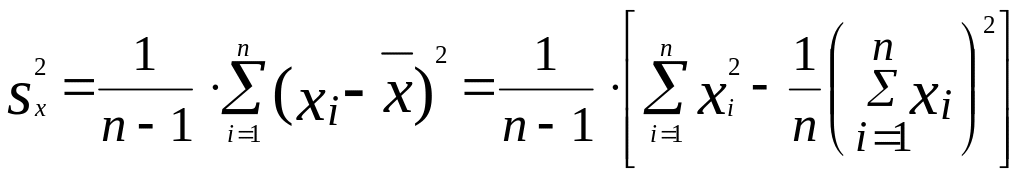
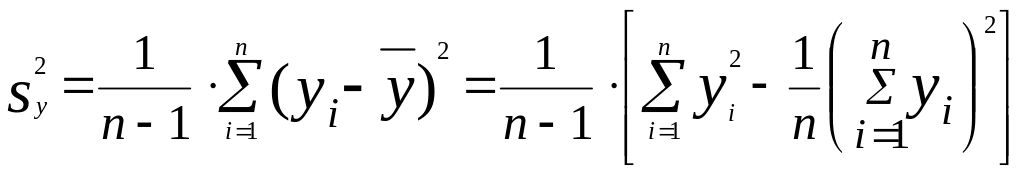
Выборочный коэффициент корреляции r* дает состоятельную, но смещенную оценку для коэффициента корреляции генеральной совокупности, эта оценка имеет смещение, равное .

Величина смещения убывает обратно пропорционально числу опытов и при n>50 составляет менее 1%.

Выборочный коэффициент корреляции r*_xy, так же как и r_xy – коэффициент корреляции генеральной совокупности, по абсолютной величине не превосходит единицы:

= 1

Выборочный коэффициент корреляции не изменяется при изменении начала отсчета и масштаба величин Х и У. Коэффициент корреляции одинаково отмечает долю случайности и криволинейность связи между Х и У. Зависимость между Х и У может быть близка к функциональной, но существенно нелинейной, а коэффициент корреляции будет значительно меньше единицы.

Проведем теперь анализ случайных величин, составляющих поле корреляции.

Каждому значению х соответствует не одно значение у, а ряд распределения этой величины. Проследим, как изменяются ряды распределения у с изменением х. Для этого весь диапазон изменения величины х разобьем ряд равных интервалов. Все точки, попавшие в этот интервал, отнесем к середине интервала:

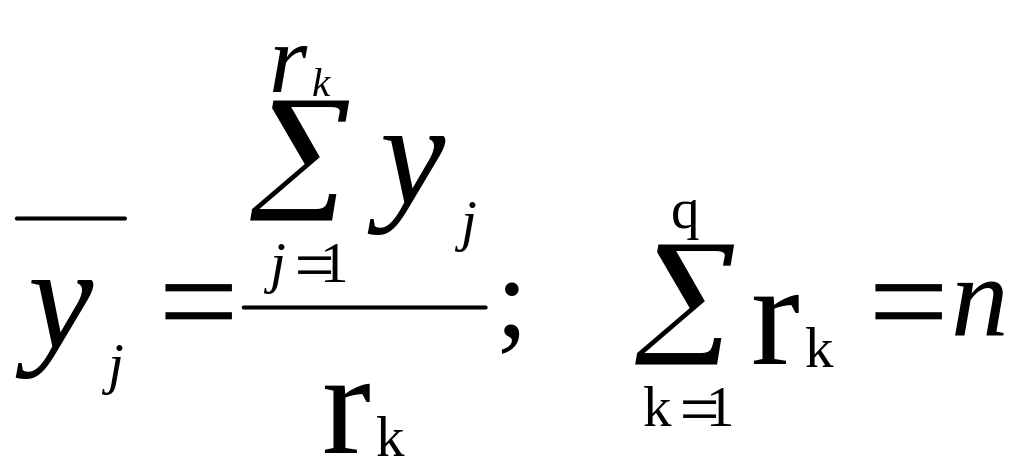
где:

– число точек, попавших в k-й интервал;

- частное среднее в интервале.

Определим частные средние в каждом интервале и соединим их ломаной линией. Полученная ломаная линия называется ломаной эмпирической линией регрессии. Она показывает, как в среднем меняется у при изменении x.

Рис.4.2. Ломаная линия регрессии.

Большим доверием будут пользоваться те интервалы, в которых больше точек. При беспредельном увеличении числа опытов n и одновременном, но не столь быстром уменьшении длины интервала x_i, эмпирическая линия регрессии сходится к теоретической линии регрессии. Нахождение параметров теоретической линии регрессии по конечному числу экспериментальных данных составляет задачу корреляционного анализа.

Процедура нахождения теоретической линии регрессии складывается из выбора формы зависимости и расчета параметров выбранного уравнения. Все вышесказанное справедливо и в отношении зависимости от многих переменных, но в этом случае говорят о гиперповерхности регрессии (поверхности отклика), а координатное пространство, в котором строят эту поверхность, называют факторным пространством. На координатных осях этого факторного пространства откладывают значения соответствующих переменных.

В случае зависимости от одной переменной, вид теоретической линии регрессии определяют по виду эмпирической линии регрессии. В случае многих переменных форму кривой регрессии заранее определить нельзя.

Чаще всего зависимость y = f(x₁,….,x_n) представляют в форме полиномов различных степеней

Примеры записей полиномов различных степеней

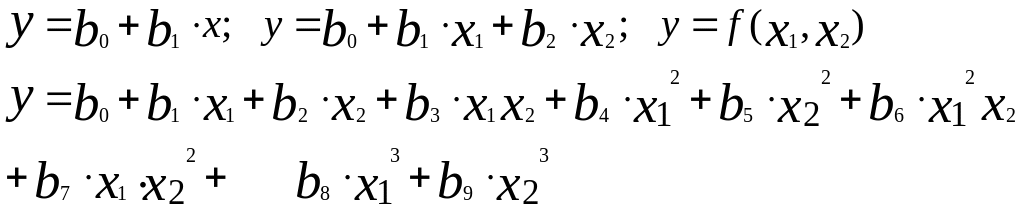
Задача корреляционного анализа – определить коэффициенты выбранного полинома так, чтобы полином наилучшим образом описывал зависимость, полученную в опыте.

Например, установлена опытная зависимость:

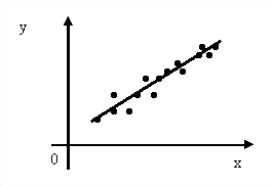
Рис. 4.3. Опытная зависимость у=f(x)

Из вида графика следует, что может подойти линейная зависимость типа

y = a₀ + a₁x_1.

Н еобходимо подобрать таким образом а₀ и а₁, чтобы линейное уравнение наилучшим образом описывало экспериментальные данные. Решение этой задачи зависит от того, что считать наилучшим. Можно потребовать, чтобы отклонение точки от прямой линии было бы минимальным, можно потребовать, чтобы

Естественно, что каждый раз результаты будут различными. Чаще всего для решения этой задачи выдвигается требования подобрать коэффициенты полинома из условия минимума суммы квадратов отклонений между экспериментальными и расчетными значениями у при соответствующих значениях х:

Это уравнение является выражением метода наименьших квадратов. Его приемущество применительно к решению задач корреляционного анализа заключается в следующем:

1. Коэффициенты определяются сравнительно просто.

2. Метод имеет достаточно хорошее вероятностное обоснование.