3.4. Моделирование равновесий в физико-химических системах

Термодинамический анализ выполняется с целью выбора оптимального технологического режима по данным о достижении равновесия для химического взаимодействия или процесса. Вероятность подхода к равновесию для системы, находящейся в стандартном состоянии, оценивается по величине стандартного изменения энергии Гиббса ΔG⁰_T. При ΔG⁰_T  0 возможно самопроизвольное протекание процесса, а при ΔG⁰_T  0 процесс невозможен.

Знание условий равновесия позволяет определить главную характеристику реакции – константу химического равновесия, рассчитать теоретический выход любого продукта, степень использования реактивов, оценить оптимальные условия проведения процесса. Константа равновесия может быть определена по экспериментальным данным о равновесии в системе или по величине стандартного измерения энергии Гиббса:

, (3.9)

где: К_р – константа равновесия;

R – универсальная газовая постоянная;

Т – температура процесса, К.

Расчет стандартного изобарного потенциала реакции обычно проводится на основе уравнения

, (3.10)

с использованием приводимых в справочной литературе величин стандартных энтальпий образования ΔH⁰_f,298, стандартных энтропий S⁰_f,298, энтальпий фазовых превращений ΔH_ФП и теплоемкостей С_р веществ.

Если в интервале температур 298 ÷ Т реагирующие вещества претерпевают k фазовых превращений, то в общем случае выражения для расчетов ΔH⁰_f,T и S⁰_f,T имеют вид:

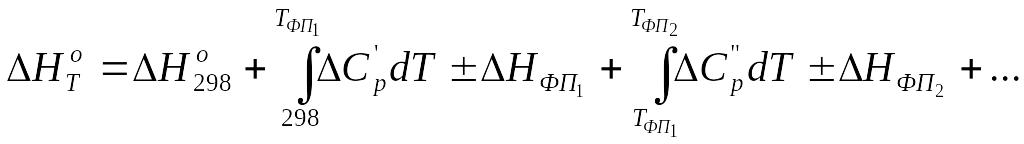
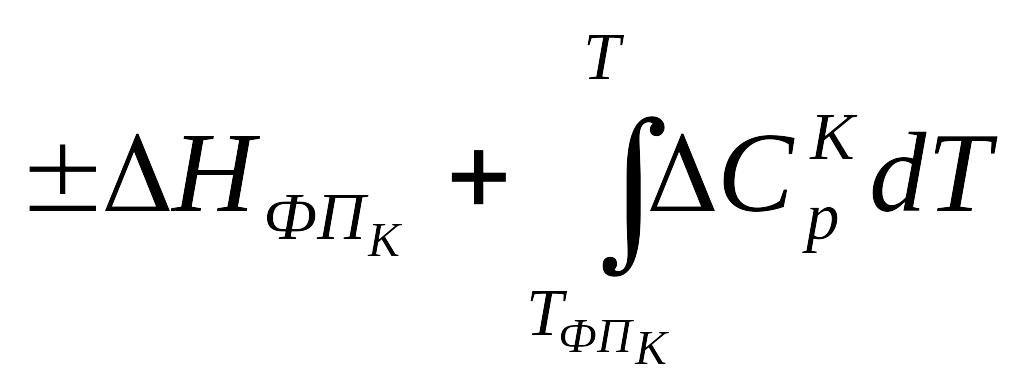, (3.11)

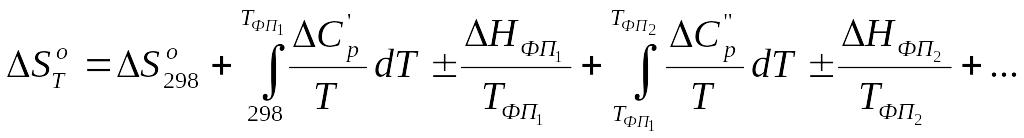
, (3.12)

В приведенных уравнениях

(3.13)

(3.14)

(3.15)

Энтальпии фазовых превращений для продуктов реакции берутся со знаком, приводимым в справочной литературе; для исходных веществ принимается противоположный знак.

Теплоемкости веществ обычно приводятся в виде интерполяционных уравнений типа

С_р = а + bТ + сТ ^-2, (3.16)

что позволяет, проведя интегрирование в общем виде, получить расчетные формулы для стандартного изменения энергии Гиббса ΔG⁰_T.

Рассчитанные значения изменения изобарных потенциалов, участвующих в реакции веществ, табулируются, после чего удобно провести их суммирование согласно формулам (3.13, 3.14,) с учетом стехиометрических коэффициентов и принадлежности веществ к исходным или конечным. По полученным значениям ΔG⁰_T.согласно уравнению (3.9) рассчитываются значения К_р. При постоянной температуре величина константы равновесия является численным выражением закона действующих масс и для реакции

(3.17)

имеет вид:

(3.18)

Последнее уравнение позволяет производить анализ равновесных соотношений компонентов при изменении активности одного из них, а также, дополняя уравнение (3.18) уравнениями материальных балансов элементов и уравнением электрического баланса, определить равновесные значения активностей индивидуальных участников химического взаимодействия. При решении вопроса о равновесном составе нескольких сопряженных реакций эту систему уравнений необходимо дополнить уравнениями частных равновесий.

Определение возможности или направления протекания процесса при данных исходных условиях основано на использовании уравнения изотермы химической реакции (изотермы Bант-Гоффа)

при Т, Р = const, (3.19)

где К_р' – величина, выражающая степень неравновесности произвольно взятой системы и рассчитываемая по уравнению (3.18) для начального значения активностей конденсированных фаз и парциальных давлений газов.

Концентрационная константа равновесия имеет самостоятельное значение для расчетов расхода реагента при извлечении металла в раствор. Например, при растворении оксидов металлов кислотами процесс описывается в общем виде следующими уравнениями:

а) для двухосновной кислоты и двухвалентного металла:

МеО_(т) + Н₂А_(р) = МеА_(р) + Н₂О, (3.20)

где А – анион кислоты.

Константа равновесия этой реакции:

. (3.21)

После достижения равновесия, когда металл практически растворится, в растворе должен остаться избыток растворителя (кислоты):

(3.22)

или (3.23)

где n_i – число молей вещества.

Кроме этого, для растворения оксида металла в соответствии с уравнением реакции (13) необходим 1 моль кислоты на 1 моль оксида. Таким образом, для полного растворения оксида металла необходимо взять кислоты в количестве на менее, чем

, . (3.24)

Минимальная исходная концентрация кислоты в растворе составит:

, (3.25)

где V – объем раствора.

б) для одноосновной кислоты и двухвалентного металла уравнение реакции имеет вид:

МеО_(т) + 2НА_(р) = МеА_2(р) + Н₂О, (3.26)

Константа равновесия этой реакции:

. (3.27)

Избыточное количество кислоты в конце реакции:

(3.28)

или

(3.29)

Кроме того, для растворения оксида металла в соответствии с уравнением реакции (3.26) необходимо иметь 2 моля кислоты на 1 моль оксида. Таким образом, для полного растворения оксида необходимо использовать кислоту в количестве не менее, чем

, . (3.30)

Исходная концентрация кислоты в растворе должна быть не менее, чем:

(3.31)

Для экспериментального определения К_с нужно взять некоторое количество исходных веществ (оксида и кислоты) и фиксировать изменение во времени концентрации исходных веществ и продуктов реакции вплоть до установления равновесия при постоянной температуре.

Величину К_с определяют графической экстраполяцией (рис. 3.5) при отношений или .