Вычитание[править | править исходный текст]

Операция вычитания из вектора   вектора   сводится к сложению первого вектора и вектора, противоположного второму:

(Само сложение при этом осуществляется так, как описано в параграфе выше, пользуясь, если это удобно, любым из приведенных там альтернативных способов).

Однако легко видеть, что из правила треугольника можно получить и отдельное геометрическое определение разности. Для этого достаточно посмотреть на чертеж, иллюстрирующий сложение по правилу треугольника и осознать, что разность векторов   и   на этом чертеже есть вектор   Отсюда прямо формулируется правило треугольника для вычитания векторов:

разность двух векторов с общим началом (или перенесенных параллельно так, чтобы начала совпали) есть вектор с началом, совпадающим с концом вычитаемого и концом, совпадающим с концом уменьшаемого.

Это правило также может быть удобным. Операция умножения вектора на число.

Сейчас разберемся как происходит умножение вектора на число.

Умножение вектора на число k соответствует растяжению вектора в k раз при k > 1 или сжатию в   раз при 0 < k < 1, при k = 1 вектор остается прежним (для отрицательных k еще изменяется направление на противоположное). Если произвольный вектор умножить на ноль, то получим нулевой вектор. Произведение нулевого вектора и произвольного числа есть нулевой вектор.

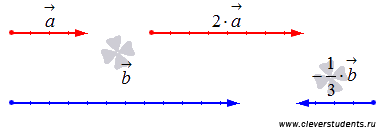
К примеру, при умножении вектора   на число 2 нам следует вдвое увеличить его длину и сохранить направление, а при умножении вектора   на минус одну треть следует уменьшить его длину втрое и изменить направление на противоположное. Приведем для наглядности иллюстрацию этого случая.

Базис B называется ортонормированным, если базисные векторы −→a,−→b,−→c единичные и  взаимноортогональные (перпендикулярные). Векторы ортонормированного базиса обозначаются −→i,−→j,−→k.

5 Вопрос

Угол между векторами — угол между направлениями этих векторов (наименьший угол).

По определению, угол между двумя векторами находится в промежутке [0°; 180°]. Угол между векторами   обозначается так:  . Если векторы перпендикулярны, то угол между ними равен 90º. Если векторы сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0^о. Если противоположно направленные векторы, то угол между ними равен 180º. Угол между двумя ненулевыми векторами находится с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними (скалярное произведение для двух векторов с координатами (x₁; y₁) и (x₂; y₂) вычисляется по формуле: x₁x₂ + y₁y₂).

Проекция вектора на ось - это число. Причем, проекция может быть положительной, если величина х_к больше величины х_н,  отрицательной,  если величина х_к меньше величины х_н  и равной нулю, если х_к равно х_н . 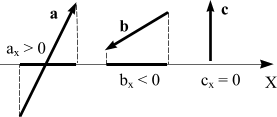Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.  Из рисунка  видно, что а_x = а Cos α то есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора. Если угол острый, то  Cos α > 0 и а_x > 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна. 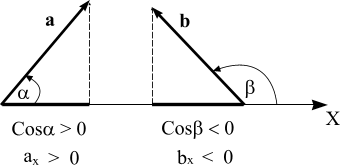Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу - отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против. Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора