Средняя гармоническая.
Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она может быть простой:
(3)
и взвешенной:
(4)
Средняя гармоническая используется в тех случаях, когда известен числитель исходного соотношения средней, но не известен знаменатель.
Пример.
Издержки производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными:
Номер завода |
Издержки производства, тыс.руб. |
Себестоимость единицы продукции, руб. |
1 |
200 |
20 |
2 |
460 |
23 |
3 |
110 |
22 |
Исчислим среднюю себестоимость изделия по трем заводам. Как и прежде, главным условием выбора формы средней является экономическое содержание показателя и исходные данные.
Издержки производства
Средняя себестоимость = ----------------------------------------
единицы продукции
(
)
Количество продукции
руб.
Пример.
Найти среднюю цену реализованных товаров по следующим данным
Вид товара |
Цена за единицу, руб. |
Сумма реализаций, руб. |
а |
50 |
500 |
б |
40 |
600 |
с |
60 |
1200 |
При расчете средней цены следует пользоваться отношением суммы реализации к количеству реализованных единиц. Нам не известно количество реализованных единиц (речь идет о разных товарах), но известны суммы реализаций этих различных товаров, т.о. следует использовать формулу средней гармонической:
(руб).
Средняя геометрическая
Средняя геометрическая определяется по формулам :
невзвешенная
(5)
взвешенная
(6)
Наибольшее распространение этот вид средней получил в анализе рядов динамики, когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000).
Степенные средние второго и более высоких порядков.
Средняя квадратическая величина.
Формула простой средней квадратической
(7)
Формула взвешенной средней квадратической
(8)
Средняя кубическая величина.
Формула простой средней кубической
(9)
Формула взвешенной средней кубической
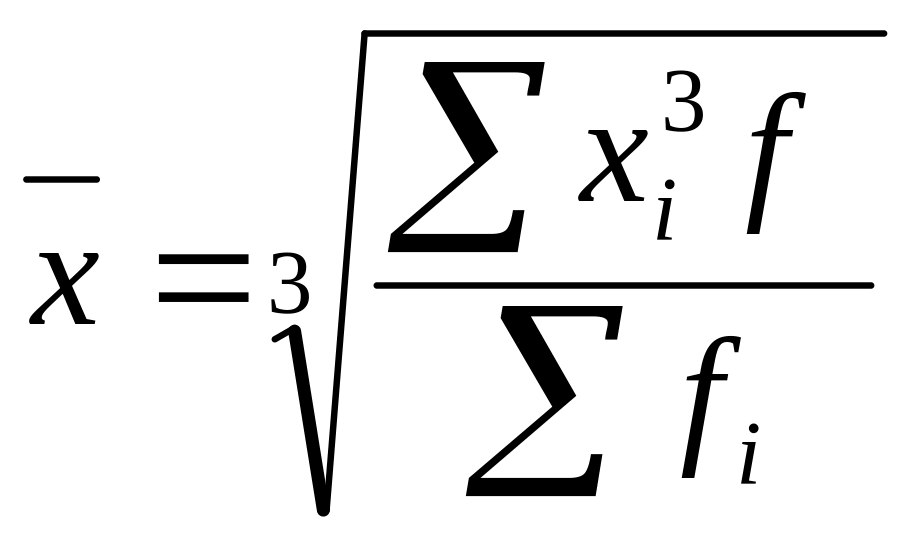(10)
Основной сферой применения степенных средних второго и более высоких порядков является измерение вариации признака в совокупности, расчет показателей взаимосвязи, структурных изменений, асимметрии и эксцесса.
В итоге можно сказать, что от правильного выбора вида средней величины в каждом конкретном случае зависит успешное решение задач статистического исследования. Выбор средней предполагает такую последовательность:
а) установление обобщающего показателя совокупности;
б) определение для данного обобщающего показателя математического соотношения величин;
в) расчет средней с помощью соответствующего уравнения.