21.2. Метод скользящих средних
Суть метода заключается в том, что фактические уровни ряда заменяются средними уровнями, вычисленными по определённому правилу, например:
— исходные или
фактические уровни ряда динамики
заменяются средними уровнями:
;
;
;
.........;
В результате
получается сглаженный ряд, состоящий
из скользящих пятизвенных средних
уровней
.
Между расположением уровней
и
устанавливается соответствие:
|
|
|
|
… |
|
|
|
- |
- |
|
|
… |
|
- |
- |
Т.о. сглаженный
ряд короче исходного на число уровней
,
где k - число уровней, выбранных для
определения средних уровней ряда.
Сглаживание методом скользящих средних можно производить по трем, четырём, пяти или другому числу уровней ряда, используя соответствующие формулы для усреднения исходных уровней.
Полученные при этом средние уровни называются трёхзвенными, четырёхзвенными, пятизвенными скользящими средними и т.д.
При сглаживании
ряда динамики по чётному
числу уровней
выполняется дополнительная
операция,
называемая центрированием,
поскольку, при вычислении скользящего
среднего, например по четырём уровням,
относится к временной точке между
моментами времени, когда были зафиксированы
фактические уровни
и
.
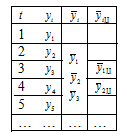
Схема вычислений и расположений уровней
сглаженного ряда становится сложнее:
….
Метод скользящих средних не позволяет получить численные оценки для выражения основной тенденции в ряду динамики, давая лишь наглядное графическое представление.