Динамика товарооборота магазина

за 2004-2008 гг.

(цифры условные)

Годы	Объем товаро- оборота	Абсолютный прирост (тыс. руб.)		Темп роста, %		Темп прироста, %		Абсолютное значение одного процента прироста, тыс. руб.
	тыс.руб	по сравнению с предыдущим годом	по сравнению с 2004 г.	по сравнению с предыдущим годом	по сравнению с 2004г.	по сравнению с предыдущим годом	по сравнению с 2004г.
А	1	2	3	4	5	6	7	8
2004	885,7	-	1	-	100	-	-	-
2005	932,6	46,9	46,9	105,3	105,3	5,3	5,3	8,857
2006	980,1	47,5	94,4	105,1	110,6	5,1	10,6	9,326
2007	1028,7	48,6	143	104,9	116,1	4,9	16,1	9,801
2008	1088,4	59,7	202,7	105,8	122,9	5,8	22,9	10,287
Итого	4915,5	202,7	-	-	-	-	-	-

§ 19. Средние показатели в рядах динамики

Для получения обобщающих показателей динамики социально-экономический явлений определяются средние величины:

средний уровень ряда динамики; средний абсолютный прирост; средний темп роста; средний темп прироста.

В качестве обобщенной характеристики уровней ряда динамики служит средний уровень ряда динамики . В зависимости от типа ряда динамики используются различные расчетные формулы:

Интервальный ряд абсолютных величин с равными периодами (интервалами времени):

Интервальный ряд абсолютных величин с неравными периодами

Моментный ряд с равными интервалами между датами (формула средней хронологической простой):

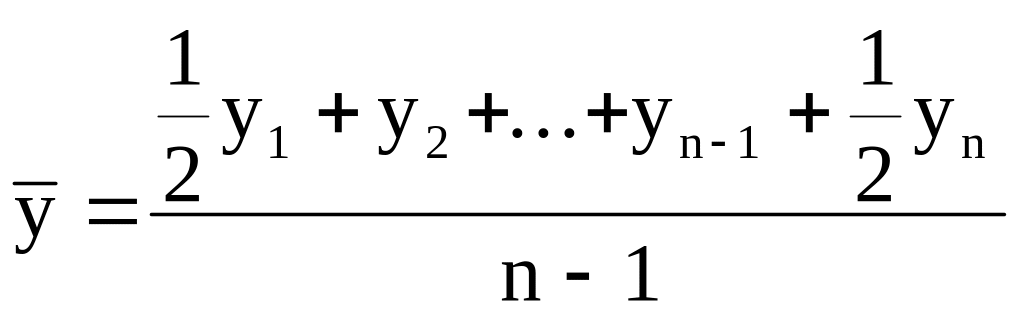
Моментный ряд с неравными интервалами между датами (формула средней хронологической взвешенной):

где

у_i - уровни ряда, сохраняющиеся без изменения на протяжении интервала времени ;

n - число уровней;

t_i - длительность интервала времени между уровнями.

Покажем расчет среднего уровня моментного ряда динамики с равноотстоящими и неравноотстоящими уровнями:

Первый пример. Если известны товарные остатки магазина на 1-ое число каждого месяца (тыс. руб.):

1/I	1/II	1/III	1/IV
18	14	16	20

то среднемесячный товарный остаток за 1 квартал по формуле (8) составит

тыс. руб.

Другой пример. Известна списочная численность рабочих организации на некоторые даты 2004 г. (чел):

1/I	1/III	1/VI	1/IX	1/I-2005
1200	1100	1250	1500	1350

Среднегодовая численность работников за 2004 г. по формуле (9) составит:

чел.

Обобщающим показателем скорости изменения явления во времени является средний абсолютный прирост за весь период, ограничивающий ряд динамики.

Средний абсолютный прирост может быть получен по одной из формул:

или ,

Обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста, показывающий, во сколько раз в среднем за единицу времени изменился уровень динамического ряда.

Средний темп роста можно определить, пользуясь формулами:

; ; ; .

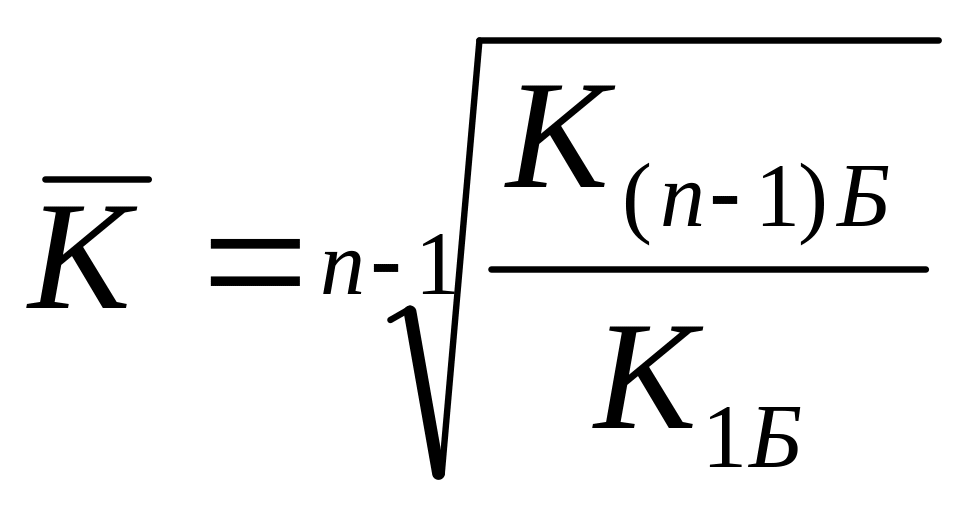Когда приходится вести расчет средних темпов роста по периодам различной продолжительности (неравноотстоящие ряды динамики), то пользуются средними геометрическими, взвешенными по продолжительности периодов. Формула средней геометрической взвешенной будет иметь вид:

где t - интервал времени, в течении которого сохраняется данный темп роста;

 - сумма отрезков времени периода.

Средний темп прироста не может быть определен непосредственно на основании последовательных темпов прироста или показателей среднего абсолютного прироста. Для его вычисления необходимо вначале найти средний темп роста, а затем уменьшить его на единицу или 100%:

или

Найдем средние показатели динамики для рассматриваемого примера (таблицы 3, 4):

среднегодовой уровень товарооборота за 2004 -2008 гг. тыс.руб.;

средний абсолютный прирост - тыс.руб.;

средний темп роста товарооборота за 2004-2008 гг.

или ( );

средний темп прироста товарооборота за 2004 - 2008гг.

.

Лекция № 7.

Статистические ряды динамики: Изучение основной тенденции в рядах динамики: методы укрупнения, скользящей средней, аналитического выравнивания