
- •I. Алгебра.
- •Матрицы и их виды.
- •2. Операции над матрицами.
- •2.1. Равенство матриц.
- •2.2. Сложение матриц.
- •2.3. Умножение матрицы на число.
- •2.4. Умножение матриц.
- •Определители второго порядка.
- •Определители третьего порядка.
- •Определители n-го порядка.
- •Обратная матрица.
- •Системы линейных уравнений. Общие понятия.
- •Система n линейных уравнений с n неизвестными и ее решение матричным способом. Формулы крамера.
- •Решение системы линейных уравнений методом гаусса.
- •Плохо обусловленные системы линейных уравнений.
- •Скалярные и векторные величины.
- •Линейные опреции над векторами.
- •Угол между векторами. Проекция вектора на ось.
- •Линейная комбинация векторов. Базис.
- •Прямоугольная декартовая система координат.
- •Линейные операции над векторами, заданными в координатной форме.
- •Пройстейшие задачи аналитической геометрии.
- •Задачи определения расстояния между двумя точками.
- •Задача деления отрезка в данном отношении.
- •Скалярное произведение векторов.
- •Свойства скалярного произведения векторов.
- •Векторное произведение векторов.
- •Смешанное произведение векторов.
- •II. Элементы аналитической геометрии. Введение.
- •Плоская линия и ее уравнение в .
- •Прямая линия на плоскости. Уравнение прямой по точке и нормальному вектору.
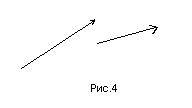
- •Уравнение прямой по точке и направляющему вектору. Пусть на плоскости дана точка и вектор (рис.4).
- •Пусть прямые и даны уравнениями и . Требуется определить угол между ними. Предположим, что прямые не перпендикулярны и вычислим . Непосредственно из рис.9 найдем, что . Тогда
- •Общее уравнение прямой.
- •Кривые второго порядка. Окружность.
- •Эллипс.
- •Гипербола.
- •Парабола.
- •Уравнение кривых второго порядка с осями симметрии, параллельными осями координат.
- •Исследование уравнения кривой второго порядка, не содержащего члена с произведением текущих координат.
- •Неравенства второй степени относительно двух переменных.
- •Поверхности и линии в пространстве .
- •Плоскость. Уравнение плоскости по точке и нормальному вектору.
- •Уравнение плоскости по трем точкам.
- •Общее уравнение плоскости.
- •Угол между плоскостями.
- •20. Прямая в пространстве . Векторное, канонические и параметрические уравнения прямой.
- •Уравнение прямой по двум ее точкам.
- •Общие уравнения прямой.
- •Угол между двумя прямыми.
- •Прямая и плоскость в пространстве .
- •Угол между прмой и плоскостью.
- •Точка пересечения прямой с плоскостью.
- •Поверхности второго порядка.
- •Цилиндрические поверхнсоти.
- •Эллипсоид.
- •Эллиптический параболоид.
- •Однополостный гиперболоид.
- •Двуполостной гипрболоид.
Скалярные и векторные величины.
ОПРЕДЕЛЕНИЕ 11.1. Величина, определяемая заданием своего численного значения, называется скалярной величиной.
ОПРЕДЕЛЕНИЕ 11.2.Величина, определяемая заданием своего численного значения и направления, называется векторной величиной.
Примерами скалярных
величин являются длина, площадь, объем,
масса, температура и др. Скалярные
величины обозначаются символами
![]() и изображаются точками соответствующей
числовой оси. Примерами векторных
величин являются сила, скорость, ускорение
и др. Векторные величины изображаются
с помощью векторов – направленных
отрезков, т.е. таких отрезков, у которых
одна из ограничивающих их точек принята
за начало вектора, а другая за его конец.
Пусть точка А
есть начало вектора, а точка В-его
конец, тогда этот вектор обозначается
символом
и изображаются точками соответствующей
числовой оси. Примерами векторных
величин являются сила, скорость, ускорение
и др. Векторные величины изображаются
с помощью векторов – направленных
отрезков, т.е. таких отрезков, у которых
одна из ограничивающих их точек принята
за начало вектора, а другая за его конец.
Пусть точка А
есть начало вектора, а точка В-его
конец, тогда этот вектор обозначается
символом
![]() и изображается с помощью стрелки (рис.4).
и изображается с помощью стрелки (рис.4).
В
B![]() .
Расстояние между началом и концом
вектора называется длиной
вектора или его
модулем. Модуль вектора
обозначается символами
.
Расстояние между началом и концом
вектора называется длиной
вектора или его
модулем. Модуль вектора
обозначается символами
![]() …
…
![]()
A
Вектор, начало
которого совпадает с его концом,
называется нулевым
и обозначается
![]() .
Нулевой вектор не имеет определенного
направления и его
.
Нулевой вектор не имеет определенного
направления и его
![]() .
.
Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.
Векторы, расположенные на одной плоскости или на параллельных плоскостях, называются компланарными.
Два вектора
![]() и
и
![]() называются равными,
если они коллинеарны, одинаково направлены
и имеют одинаковую длину. Равенство
векторов записывается в виде
называются равными,
если они коллинеарны, одинаково направлены
и имеют одинаковую длину. Равенство
векторов записывается в виде
![]() .
.
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе из одной точки пространства в любую другую его точку.
Вектор - называется противоположным вектором для вектора , если он ему коллинеарен, имеет одинаковую с длину , но направлен в противоположную сторону. Векторы и - называются взаимно противоположными векторами.
Вектор, длина
которого равна единице, называется
единичным
вектором
и обозначается символом
![]() .
.
Линейные опреции над векторами.
Операции сложения и вычитания векторов и умножения вектора на число называются линейными операциями над векторами.
ложение векторов.
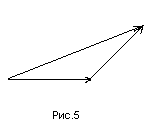
Суммой векторов
и
называется третий вектор
![]() ,
начало которого совпадает с началом
вектора
,
а конец – с концом вектора
,
при условии, что начало вектора
приложено к концу вектора
(рис.5).
,
начало которого совпадает с началом
вектора
,
а конец – с концом вектора
,
при условии, что начало вектора
приложено к концу вектора
(рис.5).
N
Q

![]()
![]()
M
P
Сумма векторов
может быть найдена и по правилу
параллелограмма (рис.6). Из определения
суммы векторов следует, что сложение
векторов подчиняется переместительному
закону
![]() .
Действительно, пусть
.
Действительно, пусть
![]() и
и
![]() есть параллелограмм. Тогда
есть параллелограмм. Тогда
![]() и
и
![]() ,
,
![]() .
Отсюда
.
.
Отсюда
.
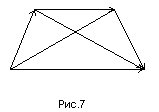
Понятие суммы
векторов, введенное для двух векторов,
можно обобщить на сумму любого конечного
числа слагаемых. Например, если заданы
три вектора
![]() и
и
![]() ,
то суммой этих векторов называется
вектор
,
то суммой этих векторов называется
вектор
![]() ,
определяемый по правилу
,
определяемый по правилу
![]() .
Аналогично, если заданы векторы
.
Аналогично, если заданы векторы
![]() ,
где
,
где
![]() ,
,
![]() ,
то суммой этих векторов называется
вектор.
,
то суммой этих векторов называется
вектор.
![]() .
.
П
N
P![]() (рис.7).
(рис.7).
![]()
![]()
M
Q![]()
Пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
Следовательно,
.
.
Следовательно,
.
Разность
векторов.
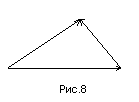
Разностью векторов
и
называется такой вектор
![]() ,
что
,
что
![]() .
Для построения вектора
.
Для построения вектора
![]() по данным векторам
и
можно воспользоваться одним из способов,
сущность которых пояснена на рис.8 и
рис.9.
по данным векторам
и
можно воспользоваться одним из способов,
сущность которых пояснена на рис.8 и
рис.9.

![]()
Умножение
вектора на число.
Пусть даны вектор
и число
![]() .
Произведением вектора
на число
называется вектор
.
Произведением вектора
на число
называется вектор
![]() ,
коллинеарный вектору
,
имеющий длину
,
коллинеарный вектору
,
имеющий длину
![]() и то же направление, что и вектор
,
если
и то же направление, что и вектор
,
если
![]() ,
и противоположное направление, если
,
и противоположное направление, если
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
.
Следствие 1.
Из определения умножения вектора на
число следует, что если
![]() ,
то векторы
и
коллинеарны. Очевидно, что если
и
коллинеарные векторы, то
.
Таким образом, два вектора
и
коллинеарны тогда и только тогда, когда
место имеет равенство
.
,
то векторы
и
коллинеарны. Очевидно, что если
и
коллинеарные векторы, то
.
Таким образом, два вектора
и
коллинеарны тогда и только тогда, когда
место имеет равенство
.
Следствие 2.
Противоположный вектор -
можно рассматривать как произведение
вектора
на
=-1,
т.е.
![]() .
.
Следствие 3. Пусть дан вектор . Рассмотрим вектор , коллинеарный , направленный, как , и имеющий длину, равную единице. Тогда, согласно операции умножения вектора на число, следует, что
![]() (33)
(33)
Умножение вектора
на число подчиняется распределительным
законам
![]() ,
,
![]() и сочетательному закону
и сочетательному закону
![]() .
.
Покажем, например,
справедливость первого из распределительных
законов. Построим на векторах
![]() параллелограмм
,
на векторах
параллелограмм
,
на векторах
![]() ,
,
![]() параллелограмм
параллелограмм
![]() (рис10). Из подобия этих параллелограммов
следует, что
.
(рис10). Из подобия этих параллелограммов
следует, что
.
N’
P’

N
M
![]()
Q
Q’
Аналогично можно убедиться и в справедливости оставшихся законов.
ПРИМЕР 12.1. Точка
является центром тяжести треугольника
![]() .
Доказать, что
.
Доказать, что
![]() .
.
Решение. Известно,
что центр тяжести треугольника находится
в точке пересечения его медиан. Обозначим
через
![]() середину стороны
середину стороны
![]() и построим вектор
и построим вектор
![]() .
Тогда, согласно операции умножения
вектора на скаляр и свойства медианы,
получим
.
Тогда, согласно операции умножения
вектора на скаляр и свойства медианы,
получим
![]() .
Построим на векторах
.
Построим на векторах
![]() и
и
![]() параллелограмм
параллелограмм
![]() (рис. 11).
(рис. 11).
B
0
A
P
D
C
Тогда, согласно
операции сложения векторов,
![]() .
Тогда
является точкой пересечения диагоналей
этого параллелограмма.
.
Тогда
является точкой пересечения диагоналей
этого параллелограмма.
Следовательно,
![]() или
или
![]() .
Итак,
.
Итак,
![]() .
Отсюда
.
Отсюда
![]() .
.
