2. Прямая линия на плоскости. Уравнение прямой по точке и нормальному вектору.

Положение прямой на координатной плоскости вполне определяется заданием:

1. любых двух точек;

2. точки и вектора, параллельного ;

3. точки и вектора, перпендикулярного ;

4. углового коэффициента и отрезка, отсекаемого прямой от оси ;

5. других величин.

Поставим задачу определения уравнения прямой в каждом из перечисленных способов ее задания.

3. Уравнение прямой по точке и нормальному вектору.

   Пусть на плоскости дана точка и вектор (рис.3). Требуется определить уравнение прямой , проходящей через точку перпендикулярно вектору (вектор  называется нормальным вектором прямой).

   В ыберем на плоскости произвольную точку и построим вектор .

y

M

M₀

x

0

l

Рассмотрим два случая:

1. пусть точка . Тогда   или

; (1)

2. если точка , то векторы и не перпендикулярны. Следовательно, или . Из 1) и 2) и определения 1.1 уравнения плоской линии следует, что уравнение (1) является уравнением искомой прямой .

Уравнение (1) называется уравнением прямой по точке и нормальному вектору .

ПРИМЕР2.1. Найти уравнение прямой , проходящей через точку перпендикулярно вектору .

Решение. Уравнение прямой будем искать в виде . По условию . Тогда для получим .

4. Уравнение прямой по точке и направляющему вектору. Пусть на плоскости дана точка и вектор (рис.4).

y

l

M

M₀

0

x

Требуется определить уравнение прямой , проходящей через точку параллельно вектору (вектор  называется направляющим вектором прямой).

Выберем на плоскости произвольную точку и построим вектор .

Рассмотрим два случая:

1. пусть точка . Тогда . Следовательно, векторы и коллинеарны. Итак, , где -некоторое действительной число. Тогда 

; (2)

2. пусть точка . Тогда  ни при каком . Отсюда и . Из 1) и 2) и определения 1.1 уравнения линии следует, что уравнение (2) является уравнением искомой прямой . Уравнение (2) называется уравнением прямой по точке и направляющему вектору . Его также называют уравнением прямой.

Замечание. Если прямая проходит через точку и параллельна оси , то направляющий вектор также параллелен этой оси. Следовательно, . Хотя его проекция , уравнение этой прямой условились записывать в канонической форме, т.е. . Последнее уравнение считается другой формой записи уравнения этой прямой . Аналогично каноническое уравнение вида означает другую форму записи уравнения прямой , проходящей через точку параллельно оси .

5. Уравнение прямой по двум точкам.

   Пусть на плоскости даны две точки , и требуется найти уравнение прямой , проходящей через эти точки (рис.5). Согласно формуле (2) уравнение любой прямой, проходящей через точку , запишется в виде

, (3)

где и - проекции неизвестного направляющего вектора этой прямой.

y

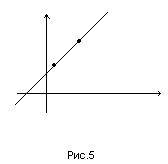
M₂

M₁

0

x

Примем за направляющий вектор вектор . Тогда , . Подставляя найденные числа в уравнение (3), получим уравнение искомой прямой .

. (4)

Уравнение (4) называется уравнением прямой, проходящий через две данные точки.

ПРИМЕР 4.1. Найти уравнение прямой, проходящей через точки и .

Решение. Полагая в (4) , получим искомое уравнение .

6. Уравнение прямой по точке и угловому коэффициенту.

   Пусть на плоскости проведена некоторая прямая (рис.6). Углом наклона прямой к оси называется угол, на который нужно повернуть вокруг начала координат против движения часовой стрелки ось абсцисс так, чтобы она стала параллельна данной прямой. Тангенс угла наклона прямой называется угловым коэффициентом прямой и означается буквой . Итак,

y

(5)

0

x

Заметим, что если острый угол, то , если тупой, то , если , то , если , то не существует.

Пусть требуется найти уравнение прямой , если проходит через точку и имеет угловой коэффициент . Согласно формуле (2) уравнение любой прямой, проходящей через точку , запишется в виде

,

где и есть координаты направляющего вектора . В качестве направляющего вектора прямой примем единичный вектор , составляющий с осью тот же угол , что и прямая .

y

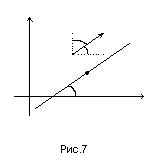
M₀

0

x

Так как , то . Полагая , получим



 . (6)

Уравнение (6) называется уравнением прямой по точке и угловому коэффициенту.

7. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми.

   Пусть прямая наклонена под углом к оси и пересекает ось в точке (рис.8). Уравнение согласно формуле (6) при запишется в виде

y

. (7)

B(0:b)

0

x

Уравнение (7) называется уравнением прямой с угловым коэффициентом.

Частные случаи:

1. если , то уравнение примет вид . Это есть уравнение прямой, проходящей через начало координат;

2. если , то есть уравнение прямой, параллельной оси ;

3. если , то - уравнение самой оси .

Пусть на плоскости даны две пересекающиеся прямые и (рис.9).

y

x

0