6. Векторное произведение векторов.

ОПРЕДЕЛЕНИЕ. Векторным произведением вектора на вектор называется вектор , удовлетворяющий условиям:

1. длина вектора численно равна площади параллелограмма, построенного на векторах и , как на сторонах, т.е. ^ ;

2. вектор перпендикулярен обоим векторам и ;

3. вектор направлен в ту сторону, что если смотреть из его конца вдоль вектора, то кратчайший поворот вектора к вектору виден совершающимися против движения часовой стрелки. Векторное произведение вектора на вектор обозначается символом .

Введем декартовую систему координат и рассмотрим векторные произведения единичных векторов . Покажем, что .

Действительно, если , то по определению векторного произведения:

1) ^ ;

2)  ,  . Но и  ,  ;

3

) если смотреть с конца вектора или , то кратчайший поворот вектора к вектору виден происходящим против движения часовой стрелки (рис.23).

0

Итак, . Следовательно, .

Аналогично доказывается, что

, , , ,

. , . (60)

Повторив вышеприведенные рассуждения для произвольных векторов и можно убедиться, что векторное произведение обладает свойствами:

1) ;

2) для  ;

3) ;

4) , если или хотя бы один из векторов есть нулевой вектор;

5) .

Найдем выражение для векторного произведения векторов, заданных своими координатами. Пусть , . Тогда , согласно свойствам 2, 3, 4 и равенству (60), получим

Итак, если , , то

. (61)

ПРИМЕР 19.1. Сила приложена к точке . Определить момент силы относительно начала координат.

Решение. Пусть точка некоторая точка . Моментом силы , приложенной к точке , относительно точки называется вектор . По условию . Тогда, согласно формуле (61), получим

. Ответ: .

ПРИМЕР 19.2. Даны вершины треугольника . Вычислить площадь этого треугольника.

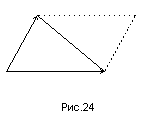
Решение. Найдем векторы (рис.24). Имеем:

B

D

.

A

C

Так как равен площади параллелограмма , то площадь треугольника найдется по формуле

Ответ: 14.

Из приведенных примеров следует, что векторное произведение в геометрии применяется при определении площадей многоугольников, в механике – при вычислении моментов.

6. Смешанное произведение векторов.

Пусть даны три вектора . Так как для векторов введены два вида произведений – скалярное и векторное, то для трех векторов относительно операции умножения существуют следующие виды произведений:

1. двойное векторное произведение, т.е. произведение, в котором вначале находится векторное произведение двух из заданных векторов, затем векторное произведение полученного вектора на третий из данных векторов.

Например, вначале находится векторное произведение , затем – векторное произведение ;

2. смешанное произведение, т.е. произведение, в котором вначале находится векторное произведение двух из заданных векторов, затем скалярное произведение полученного вектора на третий из данных векторов.

Например, вначале находится векторное произведение , затем – скалярное произведение .

Двойное векторное произведение обозначается в форме или в форме .

Ясно, что результатом двойного векторного произведения является вектор.

Смешанное или иначе векторно-скалярное произведение обозначается символом или символом . Результатом смешанного произведения является число.

Пусть требуется определить смешанное произведение векторов, если известны координаты этих векторов

, , .

Вычислим предварительно . Имеем

.

Воспользовавшись формулой (57), найдем

.

Полученное равенство, согласно теореме о разложении определителя по элементам строки, можно переписать в форме

. (62)

Формула (62) дает возможность для смешанного произведения в координатной форме. Заметим, что в этой формуле координаты векторов записаны соответственно в первой, второй и третьей строках определителя.

Покажем, что для смешанного произведения векторов справедливы равенства

. (63)

Проверим, например, справедливость равенства . Согласно формуле (62) имеем

.

Как известно, при перестановке двух строк определителя знак определителя меняется на противоположный. Тогда, умножая обе части предыдущего равенства на (-1), получим

.

Итак, .

Ф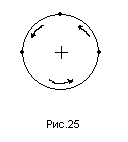 ормулы (63) проще всего запомнить с помощью правила круговой перестановки векторов, сущность которого пояснена на рис.25 и 26.

В

ыясним геометрический смысл смешанного произведения векторов . Отложим векторы от общего

h

начала и построим на этих векторах, как на ребрах, параллелепипед (рис.27). Пусть . Тогда, согласно определению векторного произведения векторов, модуль вектора равен площади gараллелограмма, построенного на векторах , как на сторонах. Следовательно,

,

где ^ и .

Обозначим через высоту параллелепипеда, опущенную из конца вектора на рассматриваемый параллелограмм, и выясним смысл произведения . Вектор перпендикулярен плоскости параллелограмма, тогда

, если и

, если .

Следовательно, если есть объем параллелепипеда, то

, если и

, если .

Итак, или . (64)

Равенство (64) означает, что модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на этих векторах, как на ребрах.

Следствие (условие компланарности трех векторов). Для того, чтобы три вектора были компланарны, необходимы и достаточно, чтобы их смешанное произведение равнялось нулю, т.е. или в координатной форме

. (65)

Необходимость. Пусть векторы компланарны. Тогда вектор перпендикулярен плоскости, в которой расположены данные векторы, следовательно, перпендикулярен вектору . Поэтому

. Следовательно, .

Достаточность. Пусть таковы, что .

Если предположить, что векторы не компланарны, то на них можно построить параллелепипед с объемом . Но, согласно формуле (64), . Следовательно, или , что противоречит исходному утверждению.

ПРИМЕР 20.1. Вычислить объем треугольной пирамиды с вершинами в точках .

Решение. Построим три вектора

с общим началом точкой . На этих векторах, как на ребрах, построим параллелепипед. Его объем равен . Объем пирамиды составляет шестую долю объема параллелепипеда. Следовательно,

Ответ: 3.

Из геометрического смысла смешанного произведения векторов и рассмотренного примера следует, что оно широко используется при вычислении объемов любых многогранников.