6. Прямоугольная декартовая система координат.

Пусть в пространстве векторы образуют базис этого пространства. Выберем в произвольную точку и отложим с началом в этой точке базисные векторы. Совокупность точки и трех базисных векторов называется системой координат в пространстве . Ввиду произвольности выбора точки и выбора базисных векторов в можно построить бесконечное множество систем координат. Выберем за базисные векторы три взаимно перпендикулярных единичных вектора . Совокупность точки и базисных векторов называется прямоугольной декартовой системой координат в пространстве .

Выберем в произвольную точку и построим вектор . Так как векторы образуют базис, то согласно (38) вектор можно разложить на компоненты по этому базису:

, (39)

где - координаты вектора в заданном базисе.

Проведем через точку в направлении векторов оси соответственно и спроектируем вектор на каждую из осей (рис.18).

z

M₃

M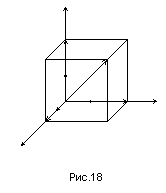

0

M₂

y

M₁

x

Пусть точки есть проекция точки на оси абсцисс, ординат и аппликат соответственно. Тогда

. (40)

Из сравнения (40) с (39) следует, что координаты вектора определяются по формулам

. (41)

В прямоугольной декартовой системе эти координаты принято обозначать через соответственно и называть прямоугольными декартовыми координатами вектора или декартовыми координатами точки . Итак,

. (42)

Координаты точки записываются в форме . Пусть вектор задан в координатной форме . Так как этот вектор совпадает с диагональю прямоугольного параллелепипеда (рис.18), то его длина равна длине этой диагонали. Следовательно,

. (43)

Обозначим через углы между вектором и осями координат . Тогда из прямоугольных треугольников, получим

, ,

. (44)

Косинусы углов , определяемые по (44), называются направляющими косинусами вектора . Нетрудно проверить, что направляющие косинуса связаны между собой соотношением

.

ПРИМЕР 15.1. Доказать, что в прямоугольной декартовой системе координат векторы имеют координаты .

Доказательство. Так как векторы образуют базис прямоугольной декартовой системе координат, то  ,  ,  , . Следовательно,

.

Но .

По формуле (38) получим, что

.

Аналогично доказываются оставшиеся равенства.

6. Линейные операции над векторами, заданными в координатной форме.

Пусть векторы и заданы в координатной форме:

,

.

Непосредственно из теоремы 13.2 и 13.3 о проекциях векторов на ось и определения координат вектора (38) вытекают правила:

, если ; (46)

; (47)

; (48)

, где . (49)

ПРИМЕР 16.1. (Условие коллинеарности двух векторов).

Установить условие коллинеарности векторов и , если , .

Решение. Так как векторы коллинеарны, то , где - некоторое число. Согласно (46)-(49) имеем

. (50)

Легко проверяется, что если координаты векторов удовлетворяют равенствам (50), то . Равенства (50) называются условием коллинеарности двух векторов.

ПРИМЕР 16.2. (Координаты единичного вектора ).

Определить координаты единичного вектора , если .

Решение. Согласно формуле (33)

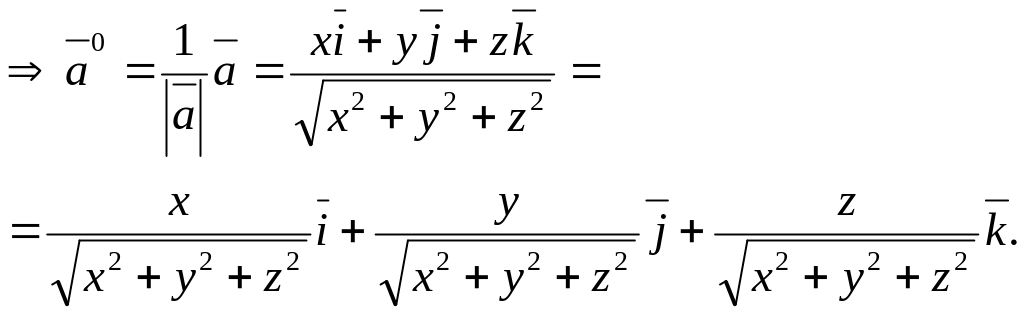
Из (44) следует, что

.