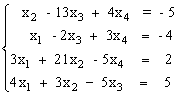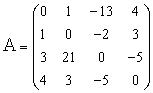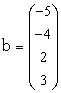Зразок виконання завдання

Тепер розглянемо рішення системи лінійних рівнянь методом оберненої матриці та методом Крамера на наступних прикладах.

ПРИКЛАД 4.1. Розв’язати систему методом зворотної матриці:

В цьому випадку матриця коефіцієнтів А і вектор вільних коефіцієнтів b мають вигляд:

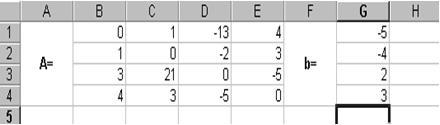
Введемо матрицю і вектор b в робочий лист MS Excel (рис. 4.1).

Рис. 4.1

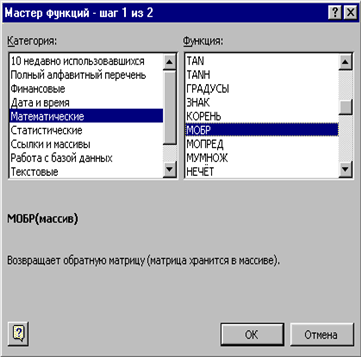
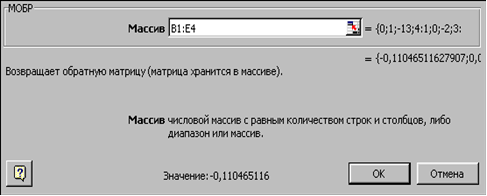
У нашому випадку матриця А знаходиться у комірках B1: Е4, а вектор B в діапазоні G1: G4. Для вирішення системи методом зворотної матриці необхідно обчислити матрицю, зворотну А. Для цього виділимо комірки для зберігання зворотної матриці (це потрібно зробити обов'язково!), Нехай в нашому випадку це будуть чарунки B6: E9. Тепер звернемося до майстра функцій, в категорії Математичні виберемо функцію МОБР, призначену для обчислення зворотної матриці (рис.4.2), клацнувши по кнопці OK, перейдемо до другого кроку майстра функцій. У діалоговому вікні, що з'являється на другому кроці майстра функцій, необхідно заповнити поле введення Масив (рис. 4.3). Це поле повинно містити діапазон комірок, в якому зберігається вихідна матриця - в ​​нашому випадку B1: E4. Дані в поле введення Масив можна ввести за допомогою клавіатури або виділивши їх на робочому аркуші, утримуючи ліву кнопку миші.

Рис. 4.2

Рис. 4.3

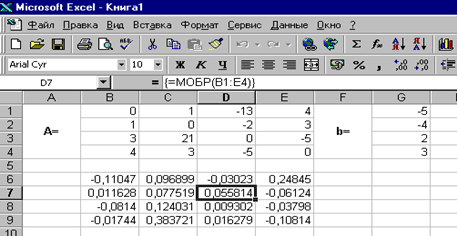
Якщо поле Масив заповнено, можна натиснути кнопку OK. У першій клітинці, виділеного під зворотну матрицю діапазону, з'явиться якесь число. Для того щоб отримати всю зворотну матрицю, необхідно натиснути клавішу F2 для переходу в режим редагування, а потім одночасно клавіші Ctrl + Shift + Enter. У нашому випадку робоча книга MS Excel матиме вигляд, що зображений на рис. 4.4.

Рис. 4.4

Тепер необхідно помножити отриману зворотну матрицю на вектор b. Виділимо комірки для зберігання результуючого вектора, наприклад H6: H9. Звернемося до майстра функцій, в категорії Математичні виберемо функцію МУМНОЖ, яка призначена для множення матриць. Нагадаємо, що множення матриць відбувається за правилом рядок на стовпець і матрицю А можна помножити на матрицю В тільки в тому випадку, якщо кількість стовпців матриці А дорівнює кількості рядків матриці В. Крім того, при множенні матриць важливий порядок співмножників, тобто АВ ≠ ВА .

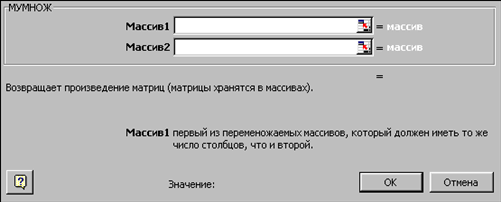
Перейдемо до другого кроку майстра функцій. Що з'явилося діалогове вікно (рис. 4.5) містить два поля введення массив1 і массив2. В поле массив1 необхідно ввести діапазон комірок, в якому міститься перша з перемножуєте матриць, в нашому випадку B6: E9 (зворотна матриця), а в поле массив2 комірки, що містять другу матрицю, в нашому випадку G1: G4 (вектор b).

Рис. 4.5

Якщо поля введення заповнені, можна натиснути кнопку OK. У першій клітинці виділеного діапазону з'явиться відповідне число результуючого вектора. Для того щоб отримати весь вектор, необхідно натиснути клавішу F2, а потім одночасно клавіші Ctrl + Shift + Enter. У нашому випадку результати обчислень (вектор х), знаходиться в комірках H6: H9.

Для того щоб перевірити, чи правильно вирішена система рівнянь, необхідно помножити матрицю на вектор х і отримати в результаті вектор b. Множення матриці на вектор х здійснюється за допомогою функції МУМНОЖ (В1: Е4; Н6: Н9), так як було описаної вище.

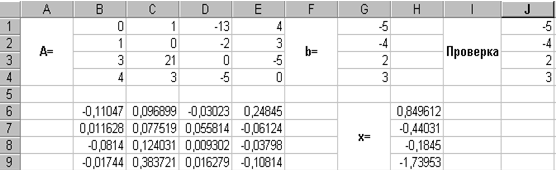
В результаті проведених обчислень робочий лист прийме вид, який зображено на рис. 4.6.

Рис. 4.6

ПРИКЛАД 4.2. Розв’язати систему з прикладу 4.1 методом Крамера.

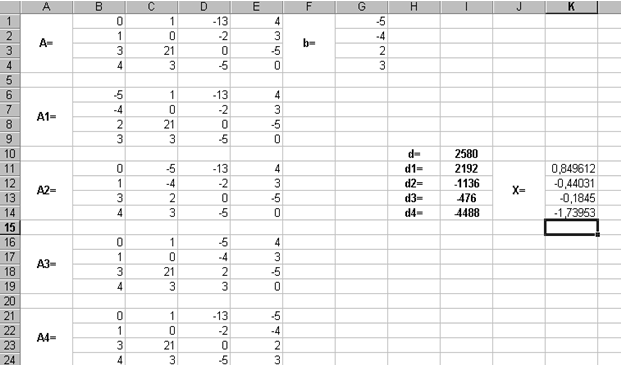
Введемо матрицю А та вектор b на робочий лист. Крім того, сформуємо чотири допоміжні матриці, замінюючи послідовно стовпці матриці на стовпець вектора b (рис. 4.7).

Для подальшого вирішення необхідно обчислити визначник матриці. Встановимо курсор в комірку I10 і звернемося до майстра функцій. В категорії Математичні виберемо функцію МОПРЕД, призначену для обчислення визначника матриці, і перейдемо до другого кроку майстра функцій. Діалогове вікно, що з'являється на другому кроці містить поле введення Масив. У цьому полі вказують діапазон матриці, визначник якої обчислюють. В нашому випадку це осередки B1: E4.

Для обчислення допоміжних визначників введемо формули:

I11 = МОПРЕД (B6: E9), I12 = МОПРЕД (B11: E14) I13 = МОПРЕД (B16: E19), I14 = МОПРЕД (B21: E24).

У результаті в комірці I10 зберігається головний визначник, а в осередках I11: I14 - допоміжні.

Скористаємося формулами Крамера і розділимо послідовно допоміжні визначники на головний. У осередок K11 введемо формулу = I11 / $ I $ 10. Потім скопіюємо її вміст в осередку K12, K13 і K14. Система розв’язана.

Рис. 4.7

ПРИКЛАД 4.3. А) Розв’язати систему рівнянь за схемою єдиного поділу:

Розв’язання.

У режимі відображення формул:

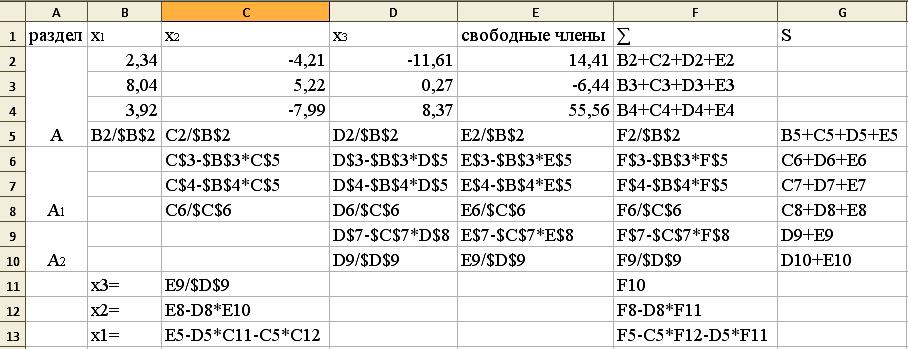
Результат:

Відповідь. x1=2,293021, x2=-4,81552, x3=0,967185.

Б) Розв’язати систему рівнянь за схемою повного ділення:

Розв’язання.

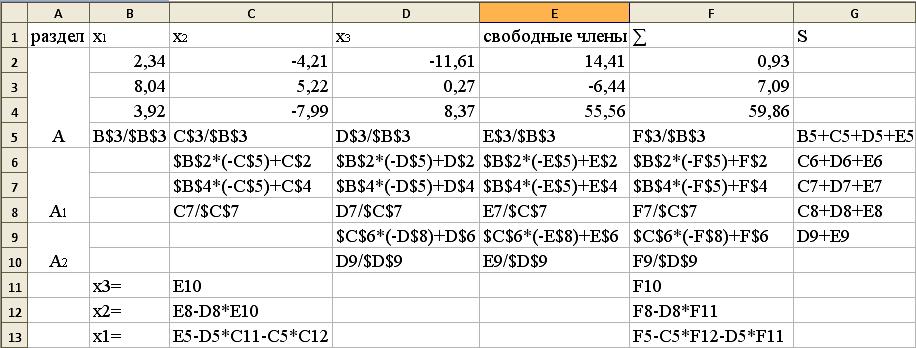
Результат:

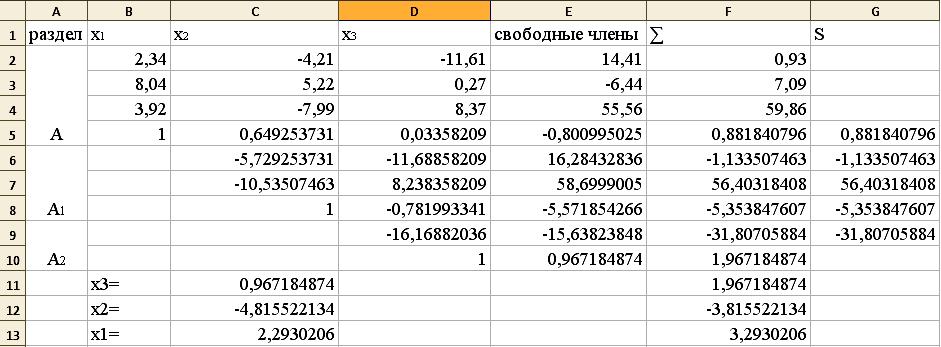
Відповідь. x1=2,2930206,x2=-4,815522134,x3=0,967184874.

ПРИКЛАД 4.4. Розв'язати систему лінійних рівнянь методом вибору головних елементів з точністю до 0,001.

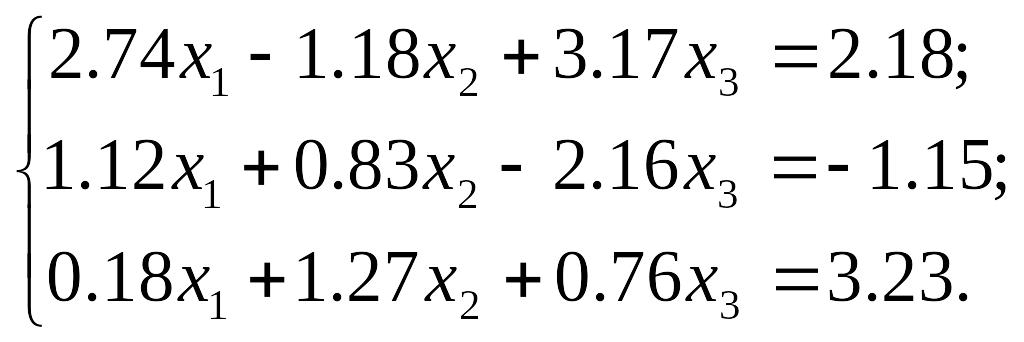
Розв’язання.

Результати обчислень занесені до таблиці:

mi	Коэфіцієнти при невідомих			Вільні члени
	X1	X2	X3
-1 0,6814 -0,2397	2,74 1,12 0,18	-1,18 0,83 1,27	3,17 -2,16 0,76	2,18 -1,15 3,23	6,91 -1,36 5,44	6,91 -1,36 5,44
-1 0,5196	2,970 -0,4768	0,0259 1,5528	– –	0,3355 2,7075	3,3485 3,7837	3,3484 3,7835
–	–	1,5569	–	2,7601	4,3181	4,3170
	0,0970	1,7728	1,2638
	1,0970	2,7735	2,2638

X₂ = ­­ ₂ =

X₁ = ₁ =

X₃ =

₃ =

Відповідь: х₁ х₂ х₃

Відповідь контрольної системи: ₁ = 1,0970; ₂ = 2.7735; ₃ = 2.2638.