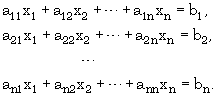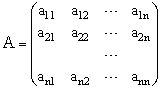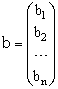Практичне заняття 4 Тема: Розв'язання систем лінійних рівнянь точними методами.

Мета. Поглибити та уточнити знання, здобуті на лекції та під час самостійної роботи з теоретичним та практичним навчальним матеріалом, сформувати вміння розв’язувати системи лінійних рівнянь різними способами, а саме, матричним методом, методом Крамера, методом Гауса та застосовувати сучасні інформаційні технології для рішення практичних завдань.

Вхідний контроль

Форма проведення вхідного контролю – фронтальне опитування за питаннями до студентів:

1. Назвати способи рішення рівнянь та систем рівнянь.

2. Пояснити у чому полягає графічний спосіб знаходження невідомих.

3. У чому полягає матричний метод рішення систем лінійних алгебраїчних рівнянь?

4. У чому полягає метод Крамера?

5. Які правила розв'язання довільної системи лінійних рівнянь вам відомі?

6. У чому полягає метод Гаусса?

Короткі теоретичні відомості

Методи розв'язування систем лінійних рівнянь можна поділити на дві групи: точні й ітераційні.

Точними називають такі методи, які дають змогу знайти точний розв'язок системи за допомогою виконання скінченої кількості арифметичних операцій у припущенні, що всі обчислення виконуються точно (без округлень), а коефіцієнти системи і вільні члени - точні числа. Але на практиці всі обчислення виконуються з обмеженою кількістю десяткових розрядів, а ірраціональні коефіцієнти і вільні члени, якщо такі є, замінюються раціональними числами. Тому в процесі обчислень вдаються до округлень, а це означає, що розв'язки, які обчислюються за точними методами, фактично є наближеними числами з певними похибками (похибками округлень). До точних належать метод Гауса, матричний, метод Крамера, метод квадратних коренів тощо.

Ітераційними називають такі методи, які дають змогу знайти наближений розв'язок системи із заздалегідь указаною точністю шляхом виконання скінченої кількості арифметичних операцій, хоч самі обчислення можуть проводитись і без округлень, а коефіцієнти і вільні члени системи бути точними числами. Точний розв'язок системи за допомогою ітераційних методів можна знайти тільки теоретично як границю збіжного нескінченного процесу. Розв'язуючи системи рівнянь ітераційними методами, крім похибок округлення, треба враховувати також похибку методу. До ітераційних належать метод ітерації, метод Зейделя тощо.

У процесі вивчення різних питань економіки, природознавства, техніки тощо доводиться розв'язувати системи лінійних алгебраїчних рівнянь. Зокрема, до таких систем зводиться чисельне розв'язування лінійних диференціальних та інтегральних рівнянь. У таких системах коефіцієнти і вільні члени рівнянь - числа наближені. А це веде до появи додаткових (так званих неусувних) похибок, які треба враховувати як у процесі обчислень, так і в остаточному округленні результату.

Розглянемо точні методи рішення системи рівнянь.

Нехай задана СЛАР наступного вигляду:

Цю систему можна представити у матричному вигляді: AX = B, де

		- Матриця коефіцієнтів системи рівнянь;
	- Вектор невідомих,			- Вектор правих частин.

При виконанні роботи систему лінійних алгебраїчних рівнянь необхідно буде вирішувати методом зворотної матриці та методом Крамера. Згадаймо основні формули, що використовуються в цих методах.