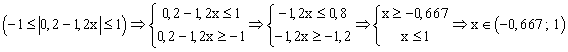Практичне заняття 3 Тема: Розв’язання нелінійних рівнянь і систем

Мета: сформувати вміння розв’язувати нелінійні рівняння та системи графічним спосом та засобами пакета Ms Excel.

Вхідний контроль

1. Назвати способи рішення рівнянь та систем рівнянь.

2. Пояснити у чому полягає графічний спосіб знаходження невідомих.

3. Постановка завдання вирішення нелінійних рівнянь. Основні етапи рішення задачі.

4. Навести інструментальні засоби для рішення рівнянь та систем рівнянь.

Теоретичні відомості

Графічний спосіб знаходження коренів рівнянь використовується рідко, бо похибка розв’язку велика. Перейдемо до опису аналітичних способів розв’язання рівняння F(x)=0. Припускається, що функція f(x) неперервна на відрізку [a,b] і на ньому знаходиться хоча б один корінь. Проблема полягає в тому, що невідома кількість коренів рівняння на даному відрізку. Тому на першому етапі рекомендується знайти значення функції в n точках відрізка,

На другому етапі виконується уточнення чисельної величини кожного кореня. Для цього пропонується використовувати чисельні методи.

Побудова графіков функцій мовою програмування

Задача: побудувати графік функції y = 3 sin(x) на інтервалі від 0 до 2π.

Аналіз:

максимальне значення ymax = 3 при x = π/2

мінімальне значення ymin = -3 при x = 3π/2

Проблема: функція задана в математичній системі координат, будувати потрібно на екрані, вказуючи координати в пікселях.

Необхідно виконати перетворення координат із математичної системи координат в екранну систему координат (пікселі):

x_e = a + kx

y_e = b - ky

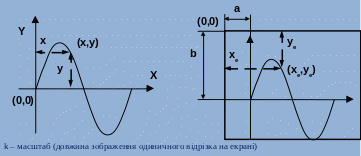
Для побудови графіка функції можна застосовувати засоби пакета Ms Excel.

Зразок виконання завдання

ПРИКЛАД 3.1. Знайти корені полінома x ³ - 0,01 x ² - 0,7044 x + 0,139104 = 0.

Для початку вирішимо рівняння графічно. Відомо, що графічним рішенням рівняння f (x) = 0 є точка перетину графіка функції f (x) з віссю абсцис, тобто таке значення x, при якому функція звертається в нуль.

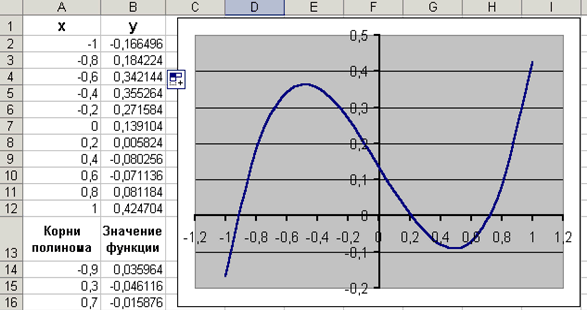
Проведемо табулювання нашого полінома на інтервалі від -1 до 1 з кроком 0,2. Результати обчислень наведені на рис. 3.1., де в клітинку В2 була введена формула: = A2 ^ 3 - 0,01 * A2 ^ 2 - 0,7044 * A2 + 0,139104. На графіку видно, що функція три рази перетинає вісь Оx, а так як поліном третього ступеня є не більше трьох речових коренів, то графічне рішення поставленої задачі знайдено. Інакше кажучи, була проведена локалізація коренів, тобто визначені інтервали, на яких знаходяться корені даного полінома: [-1, -0.8], [0.2,0.4] та [0.6,0.8].

Рис. 3.1

Тепер можна знайти коріння полінома методом послідовних наближень за допомогою команди Сервіс Підбір параметра. Відносна похибка обчислень і граничне число ітерацій (наприклад, 0,00001 і 1000) задаються на вкладці Сервіс Параметри.

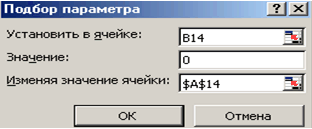
Після введення початкових наближень і значень функції можна звернутися до пункту меню Сервіс Підбір параметра і заповнити діалогове вікно наступним чином (див. рис. 3.2).

Рис. 3.2

В поле Встановити в комірці дається посилання на клітинку, в яку введена формула, що обчислює значення лівої частини рівняння (рівняння повинно бути записано так, щоб його права частина не містила змінну). У полі Значення вводимо праву частину рівняння, а в полі Змінюючи значення клітинки дається посилання на клітинку, відведену під змінну. Зауважимо, що вводити посилання на клітинки в поля діалогового вікна Підбір параметрів зручніше не з клавіатури, а клацанням на відповідній комірці.

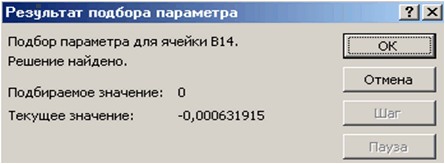
Після натискання кнопки ОК з'явиться діалогове вікно Результат підбору параметра (див. рис. 3.3) з повідомленням про успішне завершення пошуку рішення, наближене значення кореня буде поміщено в клітинку А14.

Рис. 3.3

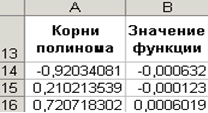
Два залишилися кореня знаходимо аналогічно. Результати обчислень будуть поміщені в осередку А15 і А16 (див. рис. 3.4).

Рис. 3.4

ПРИКЛАД 3.2. Розв’язати рівняння e ^x - (2x - 1) ² = 0.

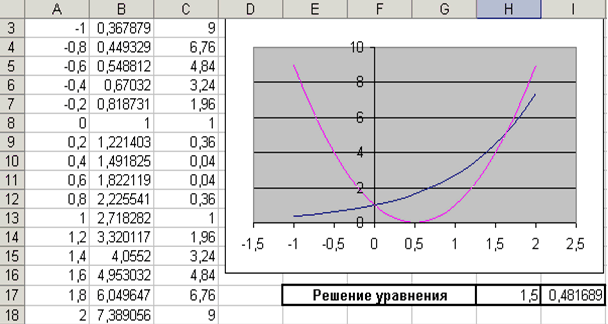
Проведемо локалізацію коренів нелінійного рівняння. Для цього представимо його у вигляді f (x) = g (x), тобто e ^x = (2x - 1) ² або f (x) = e ^x, g (x) = (2x - 1) ^2, і вирішимо графічно. Графічним рішенням рівняння f (x) = g (x) буде точка перетину ліній f (x) і g (x). Побудуємо графіки f (x) і g (x). Для цього в діапазон А3: А18 введемо значення аргументу. У осередок В3 введемо формулу для обчислення значень функції f (x): = EXP (A3), а в С3 для обчислення g (x): = (2 * A3-1) ^ 2. Результати обчислень і побудова графіків f (x) і g (x) в одній графічній області показані на рис. 3.5.

Рис. 3.5

На графіку видно, що лінії f (x) і g (x) перетинаються двічі, тобто дане рівняння має два рішення. Одне з них тривіальне і може бути обчислено точно:

Для другого можна визначити інтервал ізоляції кореня: 1,5 <x <2.

Тепер можна знайти корінь рівняння на відрізку [1.5,2] методом послідовних наближень.

Введемо початкове наближення в клітинку Н17 = 1,5, і саме рівняння, з посиланням на початкове наближення, в клітинку I17 = EXP (H17) - (2 * H17-1) ^ 2 (див. рис. 3.5).

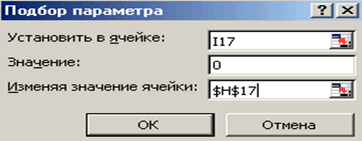
Далі скористаємося пунктом меню Сервіс Підбір параметра і заповнимо діалогове вікно Підбір параметра (див. рис.3.6).

Рис. 3.6

Результат пошуку рішення буде виведений в клітинку Н17 (див. рис. 3.7).

Рис. 3.7

ПРИКЛАД 3.3. Розв’язати систему рівнянь:

Розглянемо, як можна розв’язати систему рівнянь:

F ₁ (x) = 0, F ₂ (x) = 0, ... F _n (x) = 0

за допомогою вирішального блоку (пункт меню Сервіс Пошук Рішення), який дозволяє вирішувати не тільки оптимізаційні задачі, але і звичайні рівняння і системи рівнянь. Для вирішення цього завдання її можна сформулювати одним з таких способів:

1. Знайти мінімум (максимум) функції

при системі обмежень, заданої у вигляді рівностей F _i (x) = 0;

2. Знайти мінімум функції

В цьому випадку завдання вирішується без обмежень.

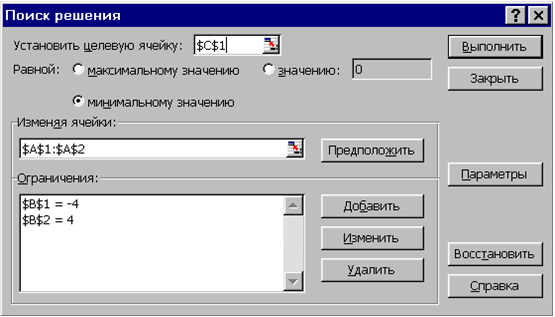
1-й спосіб. В осередку А1 і А2 вводимо числа 0 (тут ми будемо зберігати x ₁ і x _2). В осередку В1 і В2 вводимо обмеження: В1 = 2 * А1-3 * А2, В2 = А1 + А2. У осередок С1 введемо функцію мети (цей осередок ми будемо мінімізувати): С1 = СУММ (B1: B2). Скористаємося командою Сервіс Пошук Рішення і заповнимо з'явилося діалогове вікно так, як показано на рис. 7.8. В результаті рішення поставленої задачі отримаємо рішення системи вихідних рівнянь: x ₁ = 1,6, x ₂ = 2,4.

Рис. 7.8

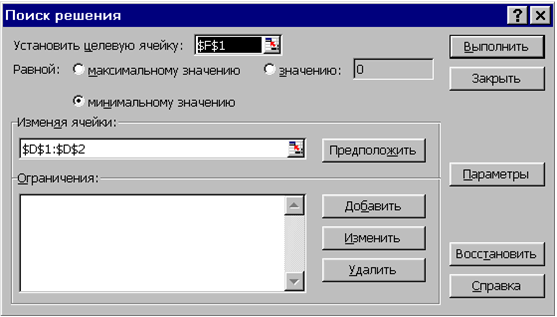
2-й спосіб. В осередках D1 та D2 будемо зберігати змінні x ₁ і x _2. В осередку E1 і E2 введемо рівняння системи: E1 = 2 * D1-3 * D2 +4, E2 = D1 + D2-4. В якості функції мети в клітинку F1 введемо формулу = E1 ^ 2 + E2 ^ 2. Звернемося до вирішального блоку (див. рис. 3.9) і введемо умову задачі оптимізації. В результаті отримуємо наступне рішення системи: x ₁ = 1,600000128, x ₂ = 2,39999949.

Рис. 3.9

ПРИКЛАД 3.4. Розв’язати систему рівнянь:

Перш ніж скористатися описаними вище методами вирішення систем рівнянь, знайдемо графічне рішення цієї системи. Відзначимо, що обидва рівняння системи задані неявно і для побудови графіків, функцій відповідних цим рівнянням, Вам потрібно включити задані рівняння щодо змінної y.

Для першого рівняння системи маємо:

З'ясуємо ОДЗ отриманої функції:

Друге рівняння даної системи описує коло.

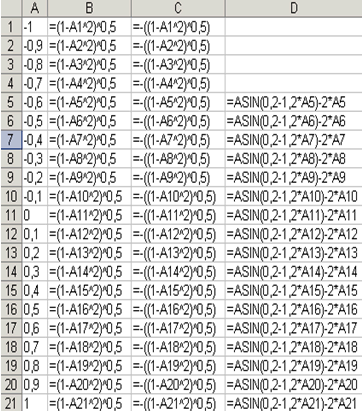
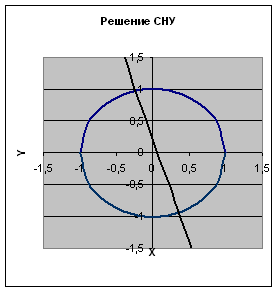
На рис.3.10 наведено фрагмент робочого листа MS Excel з формулами, які необхідно ввести в осередку для побудови ліній, описаних рівняннями системи. Точки перетину ліній зображених на рис.3.11 є графічним рішенням системи нелінійних рівнянь.

Рис. 3.10	Рис. 3.11

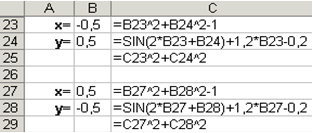
Не важко помітити, що задана система має два рішення. Тому процедуру пошуку рішень системи необхідно виконати двічі, попередньо визначивши інтервал ізоляції коренів по осях Оx і Oy. У нашому випадку перший корінь лежить в інтервалах (-0.5; 0) _x і (0.5; 1) _y, а другий - (0; 0.5) _x і (-0.5; -1) _y. Далі поступимо таким чином. Введемо початкові значення змінних x і y, формули відображають рівняння системи і функцію мети, так як показано на рис 3.12.

Рис. 3.12

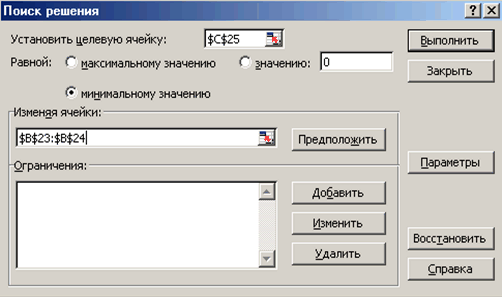
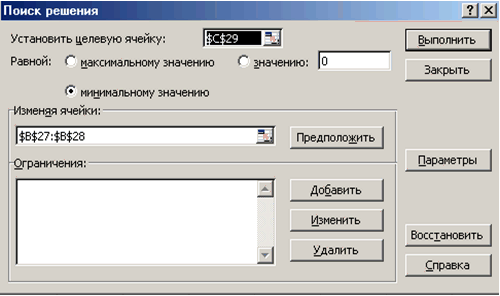
Тепер двічі скористаємося командою Сервіс Пошук рішення, заповнюючи з'являються діалогові вікна, так як показано на рис. 3.13 і 3.14.

Рис. 3.13

Рис. 3.14

На рис.3.15 наведено результати обчислень. Порівнявши отримане рішення системи з графічним, переконуємося, що система вирішена вірно.

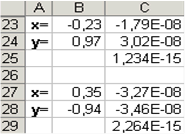
Рис. 3.15