Практичне заняття 1 Тема.Теорія похибок

Мета. Поглибити та уточнити знання, здобуті на лекції та під час самостійної роботи з теоретичним та практичним навчальним матеріалом, сформувати вміння обчислювати похибки.

Вхідний контроль

1. Назвати джерела отримання наближених чисел.

2. Дати означення абсолютної похибки наближення.

3. Яке число можна взяти за межу абсолютної похибки?

4. Сформулювати правило заокруглення чисел.

5. Дати означення відносної похибки наближення.

6. Яке число можна взяти за межу відносної похибки?

7. які цифри числа називаються значущими?

8. Як визначають вірні цифри наближеного числа?

9. Сформулювати правила дій над наближеними числами.

Теоретичні відомості Абсолютна та відносна похибки

Мірою точності наближеного числа є похибка. Розрізняють абсолютну та відносну похибку наближеного числа.

Нехай x – це наближене подання числа x₀. Тоді величина =|x – x₀| називається абсолютною похибкою подання числа x₀ за допомогою числа x. На практиці використовують максимально можливе значення – число x, що задовольняє нерівність .

х називають максимальною, або граничною абсолютною похибкою. При цьому, має виконуватися умова, що x << |x| (знак << означає “значно менше”).

Проте, абсолютна похибка не демонструє якості обчислення або вимірювання – важливе значення абсолютної похибки, що припадає на одиницю вимірювання.

Величину 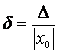називають відносною похибкою подання числа x₀ числом x. Так само як і у випадку з абсолютною похибкою, вводять поняття максимальної, або граничної відносної похибки x, що задовольняє нерівність .

На практиці використовують формулу: 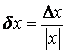. Очевидно, що << 1.

Відносну похибку зазвичай вимірюють у відсотках. Крім того, відносну похибку завжди округлюють із надлишком.

Треба зауважити, що наведені оцінки похибок наближених чисел справедливі лише, якщо запис цих чисел містить всі значущі цифри.

Значущою цифрою наближеного числа називають всяку цифру в його десятковому поданні починаючи з першої зліва ненульової цифри.

У цілому округленому числі значущими звичайно вважають всі збережені цифри. Так, в округленому числі 120 цифри 1, 2, 0 — значущі.

Проте, точність наближеного числа залежить не від кількості значущих цифр, а від кількості вірних значущих цифр.

Кажуть, що наближене значення x, що записане у вигляді десяткового дробу, має n вірних десяткових знаків у вузькому розумінні, якщо абсолютна похибка цього числа не перевершує половини одиниці n-го розряду в запису числа x.

Вірною цифрою (вірним знаком) наближеного числа а називається будь-яка його значуща цифра, для якої абсолютна похибка не перевершує половини розряду цієї цифри. Інші значущі цифри числа а називаються сумнівними.

Таким чином, якщо , то цифри числа а, починаючи з першої значущої й кінчаючи стоячою в n-м розряді після коми,— вірні, а розташовані далі—сумнівні. Наприклад, число 647,326 при =0,03 0,5 має чотири вірні цифри 6, 4, 7, 3 і дві сумнівні 2, 6.

Точність наближеного числа залежить не від кількості значущих цифр, а від кількості вірних цифр.

Остаточний наближений результат звичайно округляють до його вірних цифр, залишаючи одну сумнівну. При розрахунках з наближеними числами в проміжних результатах зберігають одну, дві, а іноді й три сумнівні цифри.

Приклад. Задані числа при зазначених абсолютних похибках округлити до вірних цифр. Визначити абсолютну похибку результату:

1) а₁ =2,6219, = 0,024; 2) а₂ = 47,35, = 1,3; 3) а₃ = 6,9971, = 0,0009; 4) а₄=0,648, = 0,04.

Розв’язання. 1) Оскільки 0,024 < 0,05, то число а₁ варто округлити до 0,1. Одержимо число а₁ 2,6 з двома вірними цифрами. Визначимо абсолютну похибку результату

= 0,024 + | 2,6219 - 2,6 | = 0,0459 0,05.

2) Оскільки 1,3 < 0,5 , то число а₂ варто округлити до десятків. Одержимо число а₂ 5•10 з однією вірною цифрою. Абсолютна похибка результату

= 1,3 + 2,65 = 3,95 4.

3) Оскільки 0,0009 < 0,005, то округлення числа робимо до 0,01. Одержимо число а₃ 7,00 з трьома вірними цифрами. Абсолютна похибка результату

= 0,0009 + | 7,00 - 6,9971 | = 0,0038 0,004.

У числі 7,00 записані нулі свідчать про три його вірні знаки й цей запис відрізняється від 7 або 7,0.

4) Оскільки 0,04 < 0,05, то число а₄ округляємо до 0,1. Одержимо число а₄ 0,6 з однією вірною цифрою. Абсолютна похибка результату

= 0,04 + 0,048 = 0,088 > 0,05,

т. е. цифра 6 уже сумнівна. Тому при округленні рекомендується залишати одну-дві сумнівні цифри, тобто

а₄ 0,65, = 0,042 0,05.

Підмітимо, що термін «вірні цифри» не слід розуміти буквально. Так, у числі 7,00, що заміняє число 6,9971, всі знаки вірні |6,9971 - 7,00| < 0,005, але жодна із цифр чисел 6,9971 й 7,00 не збігається. Однак вірні знаки наближеного числа часто збігаються з відповідними цифрами точного числа.

У деяких випадках зручно говорити, що число x є наближенням точного числа x₀ з n вірними десятковими знаками в широкому розумінні, розуміючи під цим, що абсолютна похибка x не перевищує одиниці десяткового розряду, що виражається n-ою значущою цифрою наближеного числа.