5. Квадратурна формула Гауса

Нехай функція задана на проміжку Ставиться задача: як необхідно вибрати точки і коефіцієнти щоб квадратурна формула

(7.7)

була точною для усіх многочленів найбільш можливого степеня

Оскільки в розпорядженні є сталих то ця найбільша степінь дорівнює (коефіцієнти многочлена сталих).

Теорема. Для того щоб квадратурна формула (7.7) була квадратурною формулою найвищого алгебраїчного степеня точності, необхідно і достатньо, щоб вузли збігались з нулями многочленів Лагранжа, причому така квадратурна формула єдина.

Отже, (7.8)

де нулі многочленів Лежандра.

при цьому

Залишковий член квадратурної формули Гауса де

Елементи формули Гауса подані в таблиці 7.4.

Таблиця 7.4 − Елементи формули Гауса

п	і
1	1	0	2
2	1,2		1
3	1,3
	2	0
4	1,4		0,34785484
	2,3		0,65214516
5	1,5		0,23692688
	2,4		0,47862868
	3	0	0,56888889
6	1,6		0,17132450
	2,5		0,36076158
	3,4		0,46791394
7	1,7		0,12948496
	2,6		0,27970540
	3,5		0,38183006
	4	0	0,41795918
8	1,8		0,10122854
	2,7		0,22238104
	3,6		0,31370664
	4,5		0,36268378

Приклад 1. Обчислити за формулою Гауса з

трьома ординатами

За формулою (7.8):

Результати обчислень наведені в таблиці 7.5:

Таблиця 7.5 − Результати обчислень

і
1	0,11270	1,10698	0,27778	0,30747
2	0,50000	1,41421	0,44444	0,62853
3	0,88730	1,66571	0,27778	0,46270

Точне значення

Оцінка похибки методу

де

при Тоді

Приклад 2. Обчислити 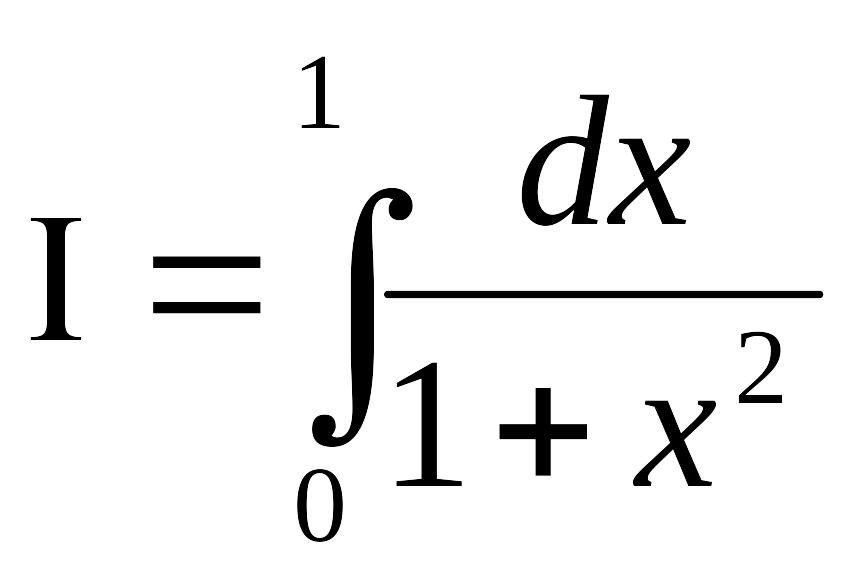за формулою Гауса з п=5. - усі знаки правильні.

Приклад 3. Обчислити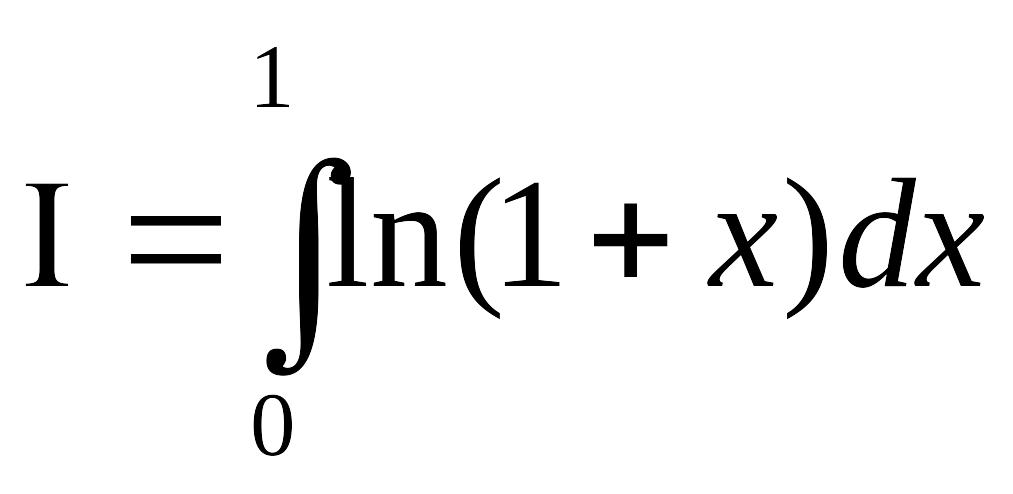 за формулою Гауса п=2. точне значення

6. Порівняння похибок квадратурних формул

Розглянуті квадратурні формули [1] мають таку структуру:

, (7.9)

де − константи, а − залишковий член. При такій самій кількості вузлів величина для різних квадратур є різною.

Приклад 1. Порівняти точність різних квадратурних формул з трьома ординатами для .

За формулою Сімпсона .

За формулою Чебишeва

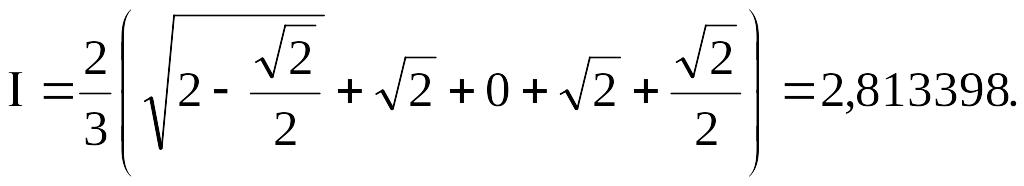
За формулою Гауса

З цього бачимо, що формула Гауса є найбільш точною. Але у конкретних випадках більш груба квадратурна формула при одному і тому самому кроці інтегрування інколи може дати більш точний результат. Точність квадратурної формули при фіксованому числі вузлів суттєво залежить від розміщення вузлів. При невдалому розміщенні вузлів квадратурна формула може дати дуже неточні результати. За наявності великої кількості нулів функції на відрізку рекомендується розбити основний відрізок інтегрування на частинні відрізки , всередині яких функції зберігають сталий знак, і виконати інтегрування на зі своїм кроком інтегрування. У більш складних випадках необхідно урахувати також поведінку похідних вищих порядків. Для сильно осцилюючих функцій необхідно застосовувати спеціальні методи обчислення інтегралів.

При знаходженні повної граничної похибки квадратурної формули (7.9) необхідно врахувати і похибку округлення. Нехай обчислені з абсолютною похибкою, яка не перевищує , а коефіцієнти обчислені точно. Тоді . Величина знайдена при .Тоді загальна похибка .

При зменшенні кроку інтегрування величина зменшується, а залишається сталою, тому існує оптимальне значення , при якому . У ряді випадків зростає зі зменшенням . У цьому випадку застосовують методи регуляризації для визначення оптимального кроку інтегрування .