Тема 6.2. Постановка задачі чисельного інтегрування. Метод прямокутників, метод трапецій, метод парабол (Сiмпсона), метод Монте-Карло – 2 год.

[1] Гл.5. п.5.4-5.11 С.282-307

_{Якщо функція неперервна на відрізку (кусково-неперервна) і відома її первісна , то визначений інтеграл за формулою Ньютона-Лейбніца 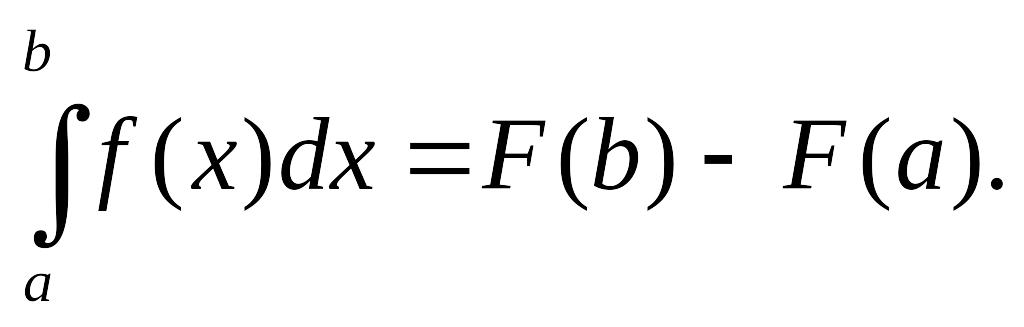У багатьох випадках первісна невідома, інколи вона досить складна або підінтегральна функція задана таблично.}

_{Задача чисельного інтегрування функції – обчислення значення визначеного інтеграла на основі ряду значень підінтегральної функції [1].}

_{Механічна квадратура – чисельне обчислення однократного інтеграла, а відповідні формули чисельного інтегрування називаються квадратурними.}

_{Механічна кубатура – чисельне обчислення двократного інтеграла, а відповідні формули чисельного інтегрування називаються кубатурними.}

_{Квадратурна (кубатурна) формула має алгебраїчний ступінь точності п, якщо залишковий член квадратурної (кубатурної) формули дорівнює 0 на множині усіх многочленів не вище п-го степеня.}

_{1. Формули Ньютона-Котеса}

_{Нехай для функції необхідно обчислити 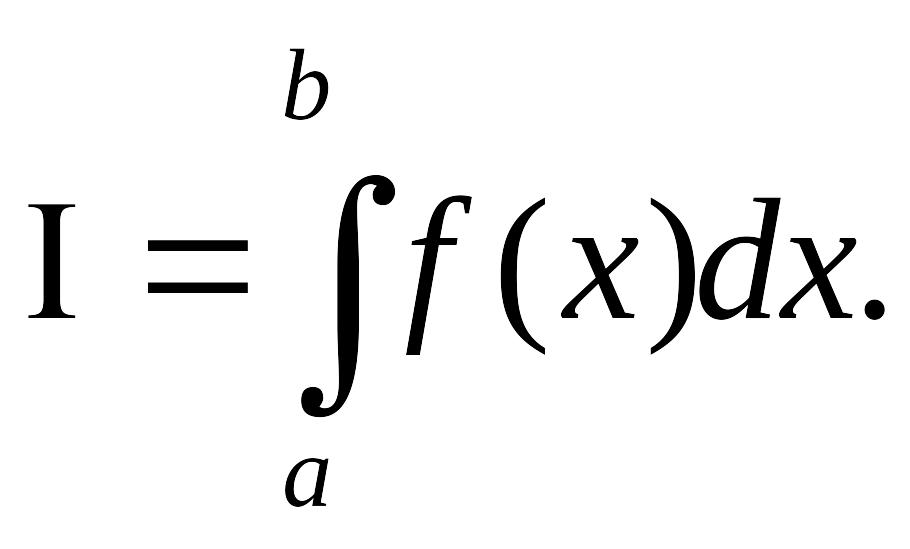Розіб’ємо відрізок на відрізки довжиною тобто Нехай Замінимо відповідним інтерполяційним многочленом Лагранжа , де визначається за (5.5). Якщо ввести позначення то}

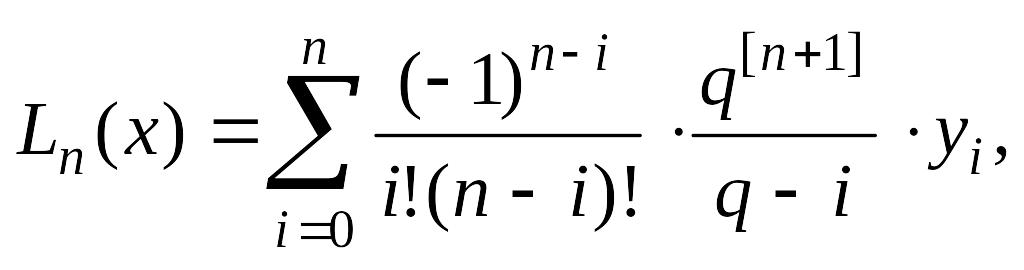_{а після інтегрування}

_{причому}

_{де коефіцієнти Котеса.}

2. Метод прямокутників

_{Інтервал розділимо на n відрізків . На кожному відрізку функція замінюється сталою . Це означає, що площа криволінійної трапеції замінюється площею прямокутника з основою і висотою (рис. 7.1).}

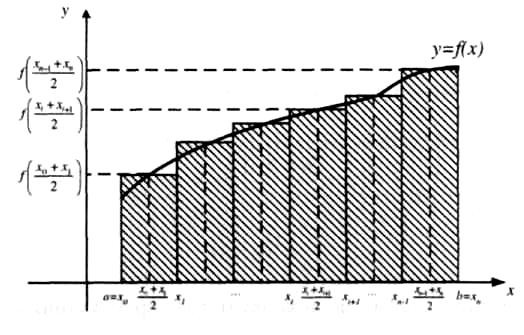
_{Рисунок 7.1 − Геометрична інтерпретація методу прямокутників}

_Тоді

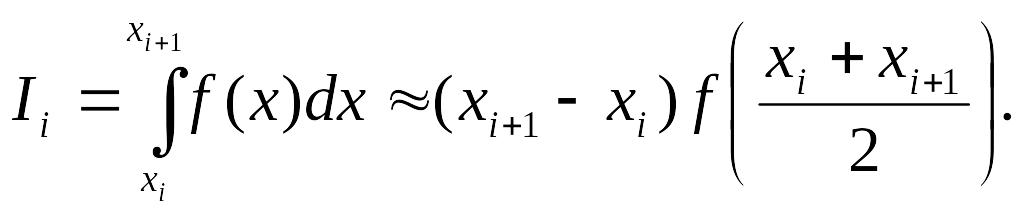
_{Якщо відрізки однакові, то введемо змінну крок обчислень, тоді}

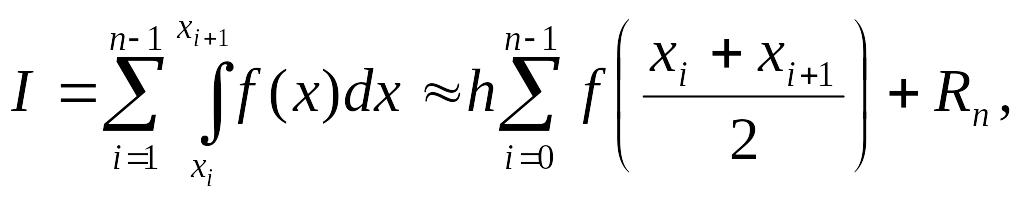_(7.1)

_{де – залишковий член або похибка квадратурної формули (7.1).}

_{Похибку методу прямокутників можна отримати з формули Тейлора}

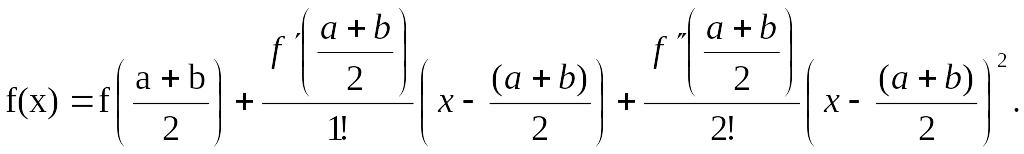
_Звідси

_{Оскільки перший інтеграл дорівнює нулю, то}

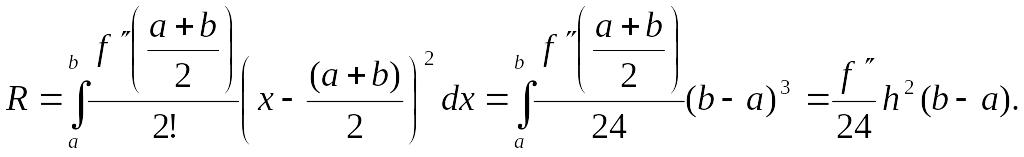
_{У результаті отримаємо похибку методу прямокутників}

_(7.2)

_де

_{Формула прямокутників дає точні результати для многочленів першого степеня.}

_{Формулу (7.1) називають також формулою середніх прямо­кутників. Якщо за висоту прямокутника взяти або , то можна отримати формули відповідно лівих і правих прямокутників.}

_{Із (7.2) випливає, що зменшення кроку інтегрування удвічі приводить до збільшення точності в чотири рази, тобто . Звідси маємо практичний спосіб (правило Рунге) оцінки похибки. Обчислюючи (7.1) з кроком 2 і потім з кроком , отримуємо , звідки}

_(7.3)

_{Приклад 1. Обчислимо , з використанням формули прямокутників, розділивши інтервал інтегрування на 10 однакових частин.}

_{Розв'язання. Позначимо .}

_{Точки поділу відрізка і значення функції в точках поділу наведені в таблиці 7.1.}

_{Таблиця 7.1 − Значення}

			метод прямокутників	метод трапецій
0	1			1
1	1,1	1,05	1,0247
2	1,2	1,15	1,0724	1,095
3	1,3	1,25	1,1180
4	1,4	1,35	1,1619	1,183
5	1,5	1,45	1,2042
6	1,6	1,55	1,2450	1,265
7	1,7	1,65	1,2845
8	1,8	1,75	1,3239	1,342
9	1,9	1,85	1,3601
10	2,0	1,95	1,3964	1,414

_{Підставимо всі значення у формулу прямокутників:}

_{Оцінимо похибку. Оскільки , то із (7.3) .}

_Отже,

_{Обчислимо для порівняння цей інтеграл за формулою Ньютона-Лейбніца}

_.

_{Отже, інтеграл , обчислений за формулою прямокутників, має три цифри після коми правильні.}