3.4. Метод простих ітерацій

Нехай відомо, що корінь рівняння лежить на відрізку .

Перетворимо рівняння (3.1.1) до вигляду

.

Таке перетворення може бути виконано різними способами, але для збіжності необхідно забезпечити виконання умови

<1.

Метод простих ітерацій або метод послідовних наближень полягає у тому, що вибираємо початкове наближення кореня рівняння, де й обчислимо перше наближення за формулою , а далі . Наступні наближення описує формула

,

Якщо існує границя , то є коренем рівняння .

Теорема 1. Нехай функція визначена та диференційована на відрізку , причому всі її значення . Тоді якщо існує правильний дріб , такий, що нерівність виконується при , то:

− процес ітерації збіжний незалежно від початкового наближення ;

− граничне значення є коренем рівняння на відрізку .

Зауваження 1. Теорема залишається правильною, якщо визначена і диференційована в нескінченному інтервалі , причому повинна задовольняти (2.8).

Зауваження 2. В умовах теореми 1 ітерації збігаються при будь-якому виборі . Окрема похибка в обчисленнях, яка не виходить за межі проміжку , не впливає на кінцевий результат. Зростає лише обсяг обчислень. Тому це надійний метод обчислень.

Теорема 2. Нехай функція визначена і диференційована на деякому відрізку , причому рівняння має корінь, який лежить у більш вузькому відрізку , де ; . Тоді якщо виконується , і початкове наближення , то:

− усі послідовні наближення знаходяться в інтервалі :=

;

− процес послідовних наближень збіжний, тобто існує

, причому − єдиний корінь на відрізку рівняння;

− виконується оцінка:

.

Зауваження 3. Нехай у деякому околі кореня рівняння похідна зберігає сталий знак і виконана нерівність <1. Тоді, якщо похідна додатна, послідовні наближення збігаються до кореня монотонно. Якщо похідна від’ємна, то послідовні наближення коливаються в околі кореня .

Метод простих ітерацій має просту геометричну інтерпретацію.

  

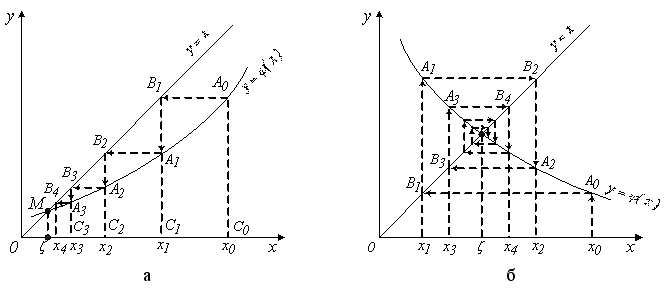
     Рисунок 3.1.4 Геометрична інтерпретація методу ітерацій

Контрольні питання для самоперевірки

1. В чому суть аналітичного методу відокремлення коренів?

2. Які теореми використовуються для аналітичного методу відокремлення коренів?

3. В чому суть алгоритму методу половинного ділення? Дайте геометричну інтерпретацію цього методу.

4. Графічна інтерпретація методу половинного ділення та основні формули методу.

5. В чому суть алгоритму методу хорд? Дайте геометричну інтерпретацію цього методу.

6. Графічна інтерпретація методу хорд та основні формули методу.

7. В чому суть алгоритму методу ітерацій? Основні формули методу.

Завдання

Опрацювати вказівки до практичного заняття. Виконати індивідуальне завдання у зошиті. Застосувати для виконання інструментальні пакети та скласти власну програму мовою програмування.