Тема 3.1. Чисельні методи рішення нелінійних рівнянь: постановка задачі, відділення коренів, метод половинного ділення, метод хорд, метод простих ітерацій. – 2 год.

[1] Гл.3,п.3.4-3.5 С. 146-167

Якщо алгебраїчне та трансцендентне рівняння досить складні, то корені рідко вдається знайти точно. Окрім того, в деяких випадках коефіцієнти відомі лише приблизно, і тому задача про точне визначення коефіцієнтів рівняння не має сенсу. Тому важливе значення мають способи приблизного знаходження коренів рівняння та оцінка степені їх точності.

Нехай задано неперервну функцію в деякому обмеженому або необмеженому інтервалі . Необхідно знайти всі або деякі корені рівняння

(3.1.1)

Корінь рівняння (3.1)– будь-яке значення , яке перетворює на нуль (тотожність (3.1.1)), тобто , або нуль функції .

Вважаємо, що (3.1.1)має лише ізольовані корені. Ця задача передбачає два етапи розв'язування:

а) відокремлення коренів, тобто виокремлення достатньо ма­лої області, що належить до області допустимих значень функції , у якій є один і лише один корінь;

б) уточнення наближеного значення кореня до наперед заданої точності.

Відокремлення коренів

Для відокремлення дійсних коренів корисно знати кількість коренів, а також нижню і верхню межі їх розміщення. Для цього використовується ряд теорем.

Теорема 1. Теорема Больцано-Коші. Якщо неперервна функція на кінцях відрізка має різні за знаком значення, тобто , то на цьому відрізку рівняння (1) має хоча б один корінь. Якщо, крім цього, існує похідна і зберігає знак, тобто або >0, то корінь єдиний.

Теорема 2. Алгебраїчний многочлен степеня

(3.1.2)

має рівно коренів, дійсних або комплексних, за умови, що кожний корінь підраховується таку кількість разів, якій дорівнює його кратність.

Теорема 3. Якщо − корінь алгебраїчного многочлена з дійсними коефіцієнтами, то також є коренем тієї самої кратності.

Наслідок. Алгебраїчний многочлен із дійсними коефіцієнтами непарного степеня має хоча б один дійсний корінь.

Теорема 4. Нехай і , де − коефіцієнти (3.1.2), . Тоді модулі всіх коренів рівняння задовольняють нерівність:

.

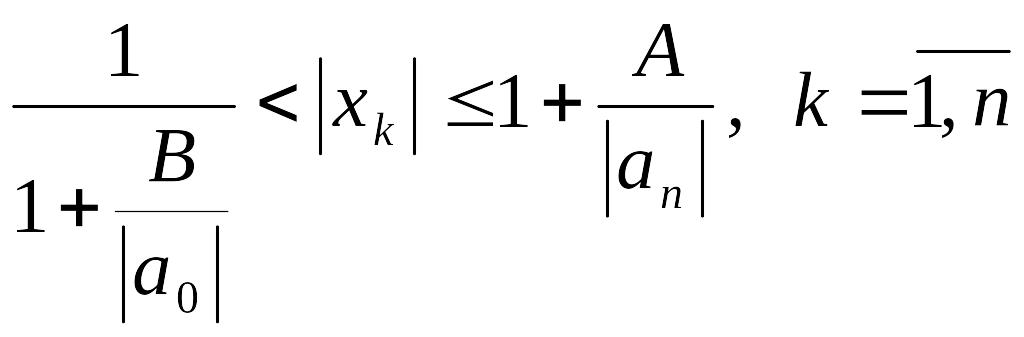На практиці застосовують такі методи відокремлення коренів: засобами комп’ютерної графіки, дослідження функцій і побудова графіка функції, застосування методу половинного поділу.

Процес відокремлення коренів починається з установлення знаків в граничних точках і області її існування. Потім за допомогою процесу половинного поділу визначають знаки функції в точках поділу.

За допомогою методу підбирання можна, застосовуючи ком­п'ютер, протабулювати функцію з певним кроком і визначити проміжки, на яких вона змінює знак.

Приклад 1. Відокремити корені рівняння .

Розв’язання. Тут . Відповідно теоремі 2 рівняння має не більше трьох дійсних коренів. Методом підбирання визначимо, що

		-3	-2	-1	0	1	2	3	+
	-	-	+	+	+	-	-	+	+

Отже, рівняння має три корені. Інтервали знаходження коренів (-3;-2), (0;1), (2;3) .

Використовують також графічний спосіб відокремлення коренів: будують графік функції і наближено визначають області, де графік перетинає вісь абсцис. Інколи зручно рівняння (3.1.1) записати у вигляді . Значеннями коренів у цьому випадку будуть абсциси точок перетину графіків функцій і .

Приклад 2. Відокремити корені рівняння .

Розв’язання. Перетворимо рівняння до вигляду і побудуємо гра­фіки функцій і . З рис. 3.1.1 випливає, що рівняння має два корені, і вони належать відповідно до проміжків: .

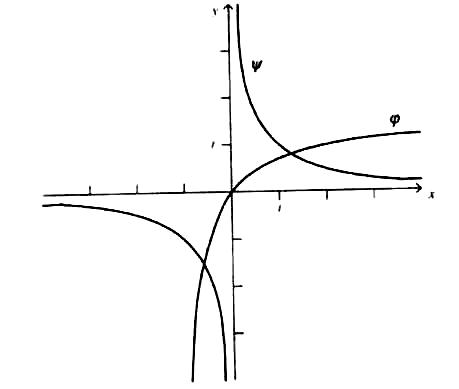
Рисунок. 3.1.1 − Графічне відокремлення коренів

Приклад 3. Відокремити корені рівняння .

Розв'язання. Тут , тому при . Звідси , . Отже, рівняння має лише два дійсні корені, один з яких є в інтервалі , а інший ― в інтервалі . Уточнюємо інтервали знаходження коренів: (-1;0) і (1;2)

Приклад 4. Відокремити корені рівняння , де . На основі теореми 4 корені знаходяться в інтервалі < < 2. Уточнюємо інтервал коренів.

	-2	-1			1	2
	-	+	+	+	+	+

Інтервал знаходження коренів (-2;-1).

Для грубої оцінки похибки використовується теорема 5.

Теорема 5. Нехай − точний, а − приблизний корені рівняння , які знаходяться на одному й тому самому відрізку , причому >0. Тоді виконується оцінк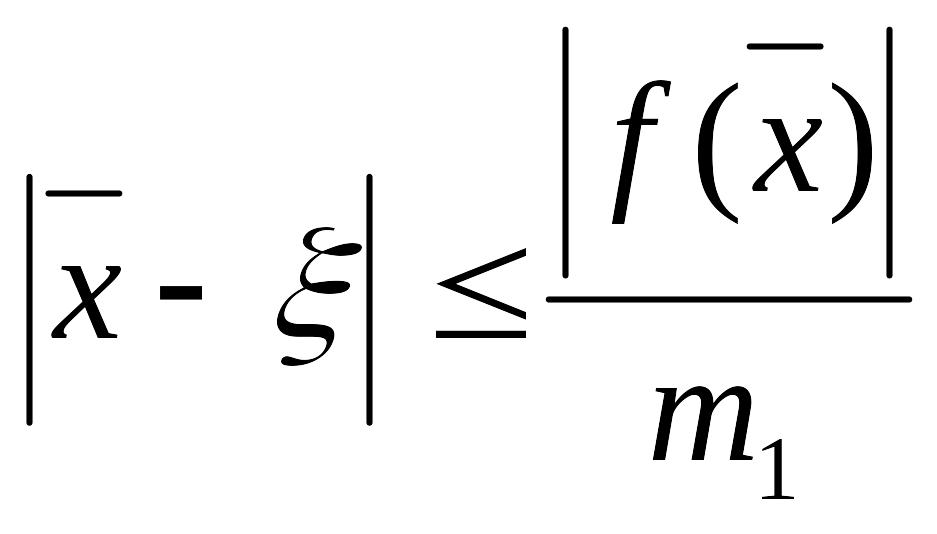а , де за можна брати .

Приклад 5. Оцінити абсолютну похибку, якщо , а .

<

Взагалі універсальних методів відокремлення коренів не існує.