Индивидуальные задания

Задача 1. Составить программу для вычисления определенного интеграла с заданной точностью указанным методом:

Номер варианта	Интеграл	Точность	Метод
1			Средних прямоугольников
2			Трапеций
3			Левых прямоугольников
4			Средних прямоугольников
5			Трапеций
6			Правых прямоугольников
7			Средних прямоугольников
8			Трапеций
9			Левых прямоугольников
10			Средних прямоугольников
11			Трапеций
12			Правых прямоугольников
13			Средних прямоугольников
14			Трапеций
15			Левых прямоугольников
16			Средних прямоугольников
17			Трапеций
18			Правых прямоугольников
19			Средних прямоугольников
20			Трапеций

Задача 2.

1. Вычислите данный интеграл вручную по формуле трапеций при и 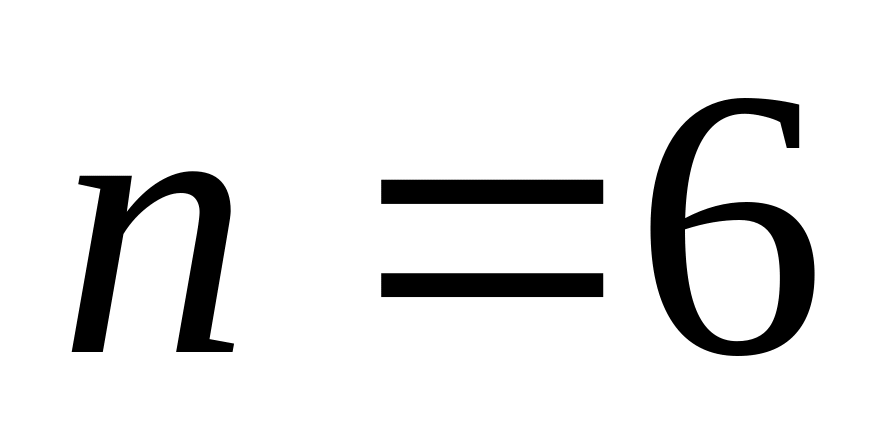. Оцените погрешность приближения 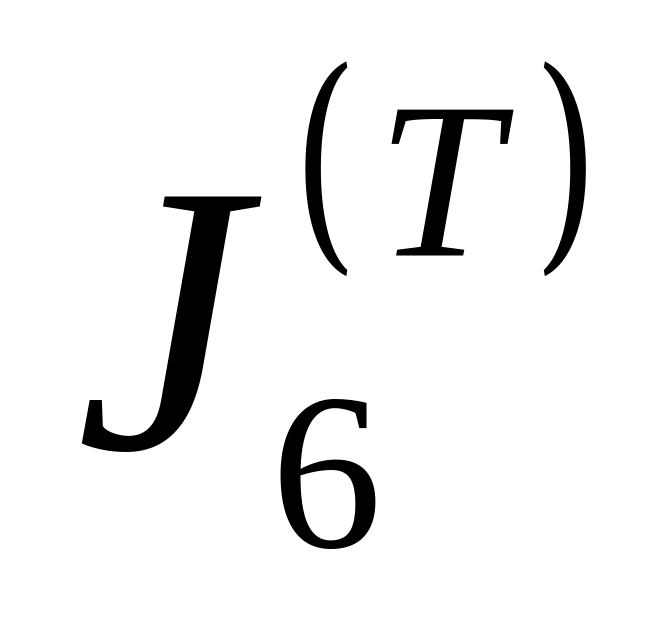методом двойного пересчёта, а затем найдите абсолютную погрешность этого же приближения по формуле строгой оценки погрешностей.

2. Вычислите данный интеграл по формуле Симпсона с точностью до

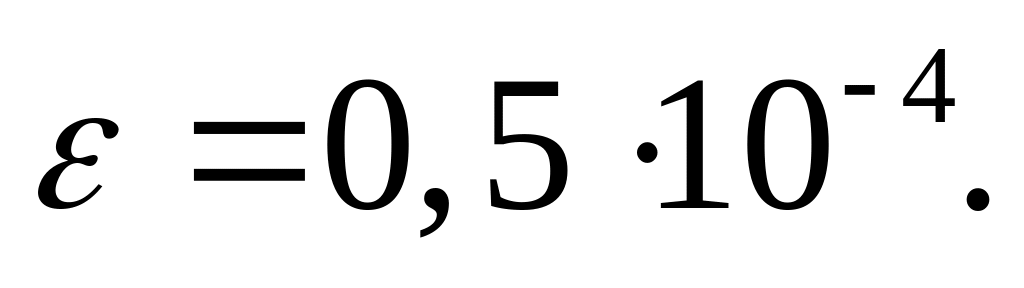
3. Вычислите интеграл по формуле Ньютона-Лейбница с максимальной точностью, которая возможна при используемых вычислительных средствах.

4. Сравните полученные разными способами результаты по их точности.

Вариант	Интеграл
1
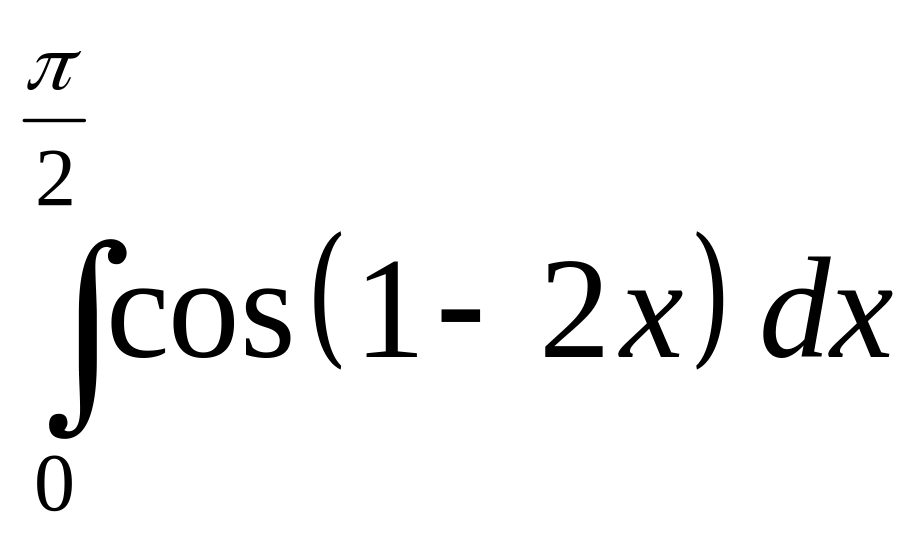
2
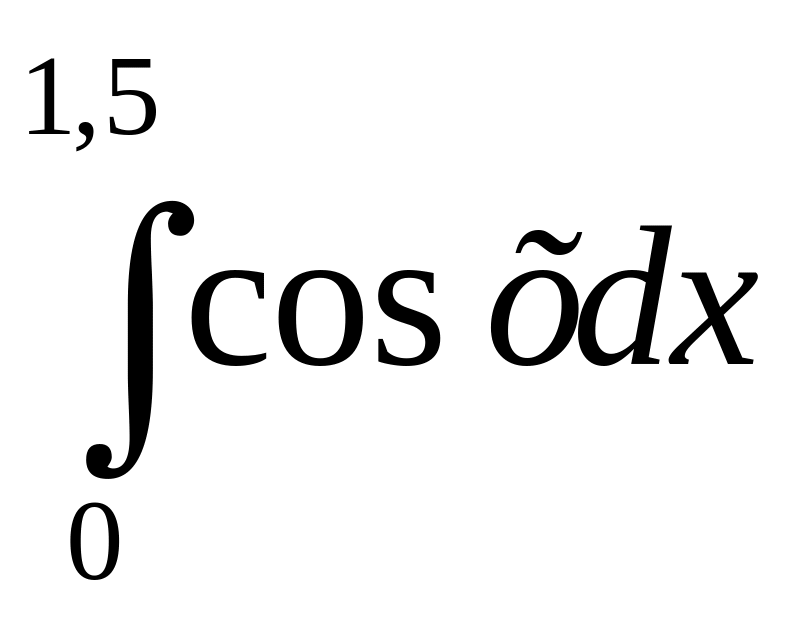
3
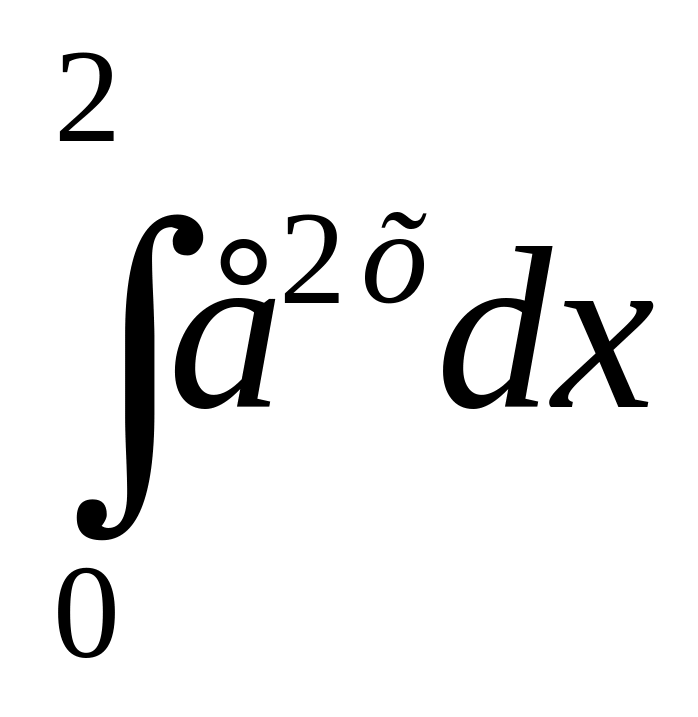
4
5
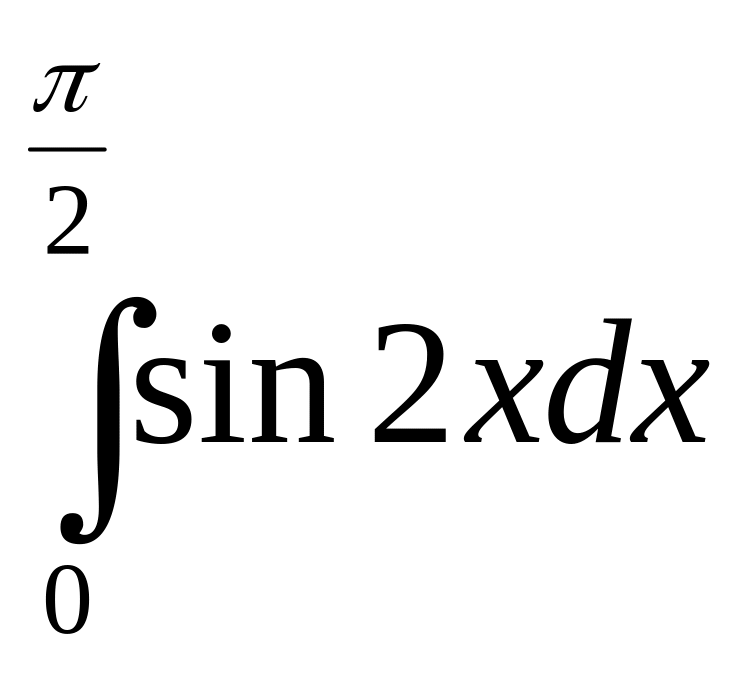
6
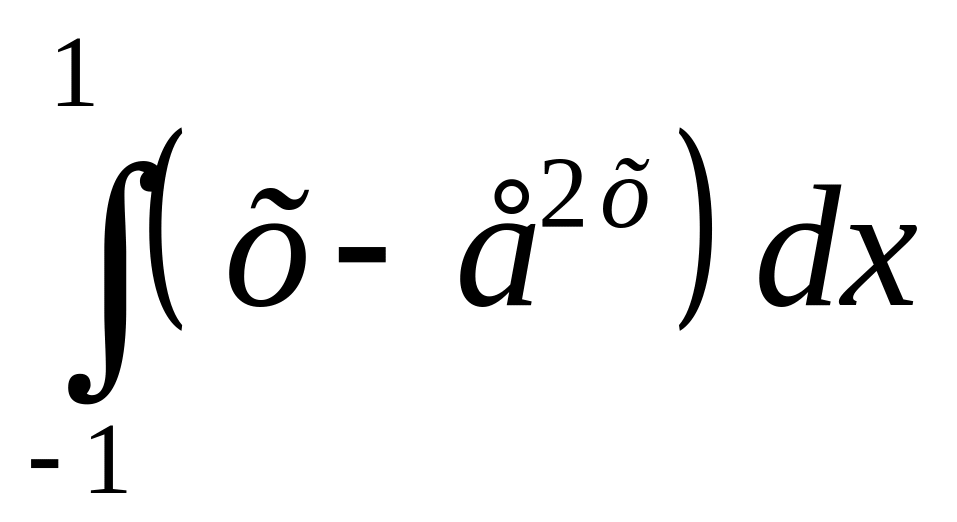
7
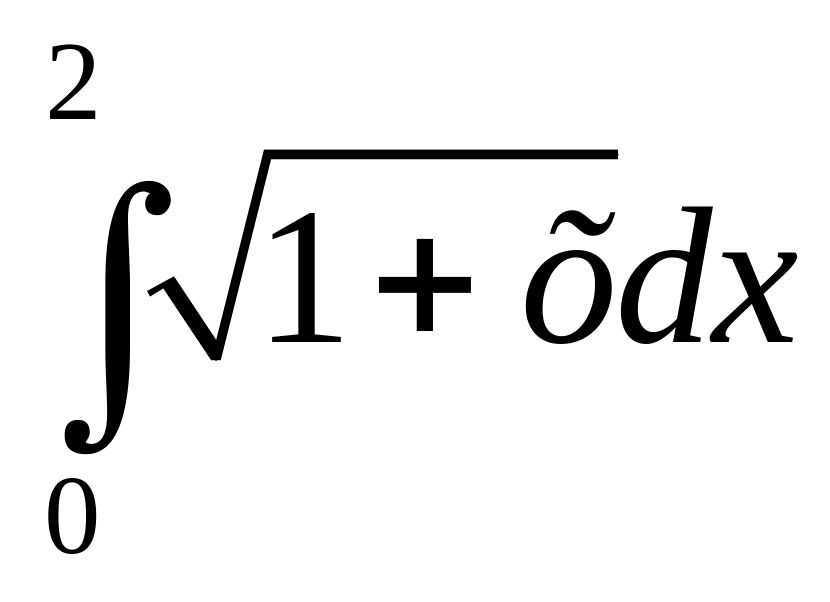
8
9
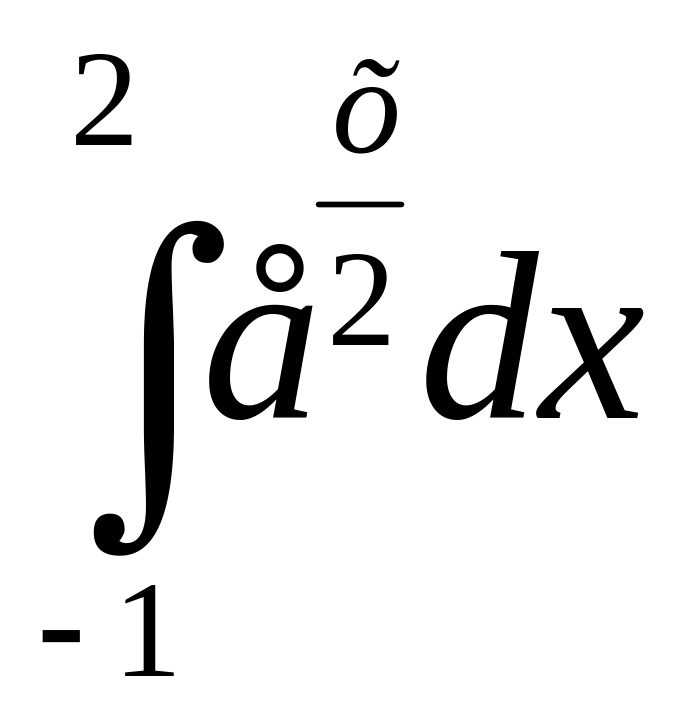
10
11
12
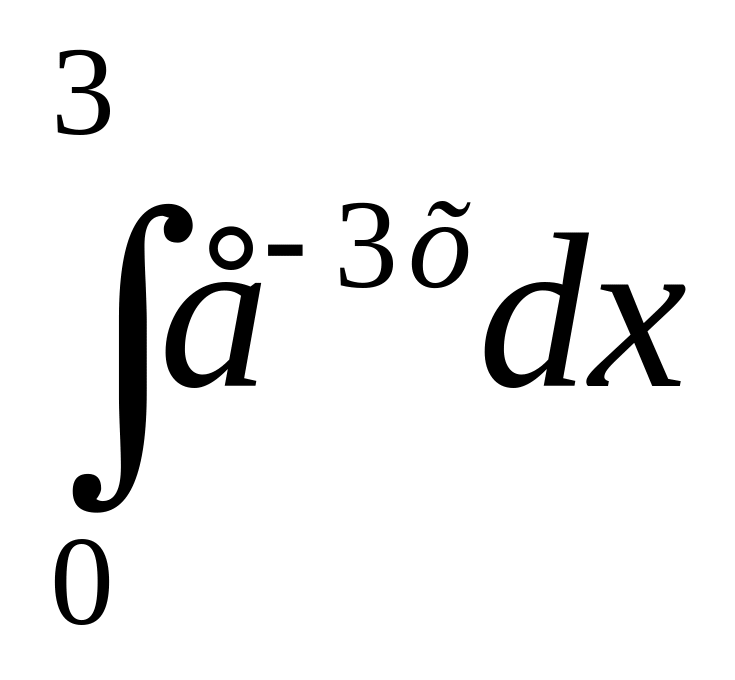
13
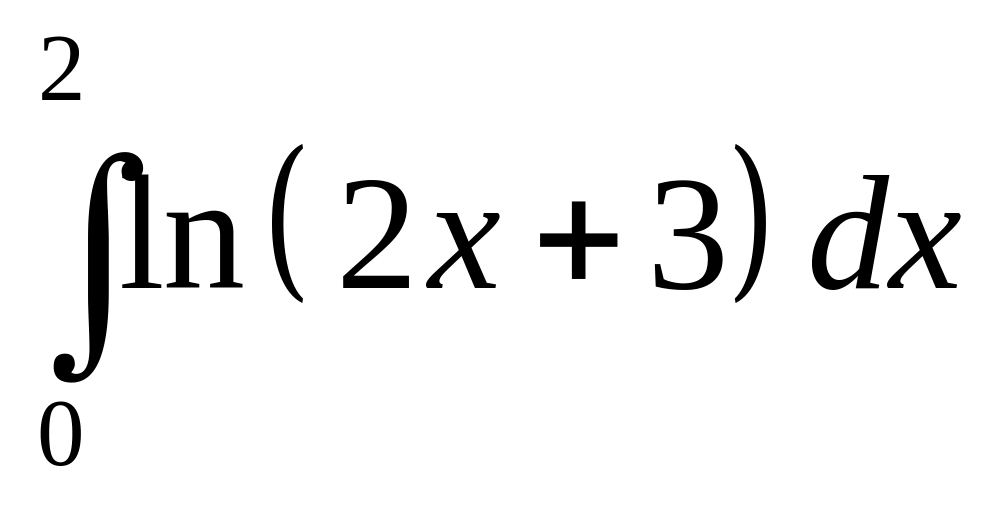
14
15

Порядок выполнения работы указан в задании. При вычислениях по формуле Симпсона сначала надо определить число , при котором формула обеспечивает точность , затем составить программу реализации формулы и с её помощью найти . Для этого, чтобы не учитывать вычислительные погрешности, шаг разбиения и значения функций следует брать с двумя запасными цифрами.

Контрольные вопросы.

1. Численный метод приближённого вычисления определённых интегралов.

2. Квадратурные формулы трапеций и Симпсона.

3. Строгая оценка погрешностей этих формул.

4. Оценка погрешностей методом двойного пересчёта.

5. Определение шага разбиения отрезка интегрирования, при котором квадратурная формула обеспечивает заданную точность.

6. Вопросы оценки точности приближённого интеграла с учётом вычислительных погрешностей.