Лабораторная работа № 7.

Тема: Вычисление интегралов при помощи формул Ньютона-Котеса.

Цель: научиться определять численное решение определенного интеграла.

Численное интегрирование

Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида

(1),

где f(x) — подынтегральная функция, непрерывная на отрезке [а; b].

Пусть задана подынтегральная функция f(х), необходимо найти определенный интеграл, который вычисляется по формуле Ньютона — Лейбница

= F(b)-F(a). (2)

Если же интеграл от данной функции не может быть вычислен по формуле (2), или если функция f(х) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления интеграла (2) существует много численных методов, таких как:

• метод прямоугольников;

• трапеций;

• Симпсона и др.

При вычислении интеграла следует помнить, каков геометрический смысл определенного интеграла.

Если f(x) 0 на отрезке [а; b], то численно равен площади фигуры, ограниченной графиком функции у = f(х), отрезком оси абсцисс, прямой х = а и прямой х = b (рис. 1). Таким образом, вычисление интеграла равносильно вычислению площади криволинейной трапеции.

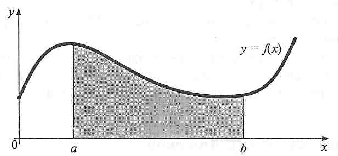
Рис. 1. Геометрический смысл интеграла

Метод прямоугольников

Разделим отрезок [а; b] на n равных частей, т. е. на n элементарных отрезков. Длина каждого элементарного отрезка . Точками деления будут: х₀ = а; x₁ = a + h; x₂ = a + 2h, ...,

х_n-1 = а + (n- 1)h; х_n = b. Эти числа будем называть узлами. Вы­числим значения функции f(x) в узлах, обозначим их у₀, у₁, у_2,, ..., у_n. Стало быть, у₀=f(а), у₁ =f(x₁), у₂ =f(х₂), ..., y_n=f(b). Числа у₀, y_1, у_2,, ..., у_n являются ординатами точек графи­ка функции, соответствующих абсциссам х_0,, х₁, х₂, ..., х_n (рис.1).

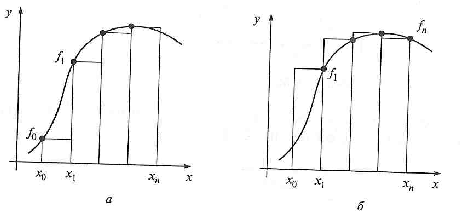
Рис. 2. Методы левых (а) и правых (б) прямоугольников

Из рис. 2. видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составлен­ного из п прямоугольников. Таким образом, вычисление опреде­ленного интеграла сводится к нахождению суммы п элементар­ных прямоугольников

(3)

(4)

Формула (3) называется формулой левых прямоугольни­ков, (4) — правых прямоугольников, (5) — формулой сред­них прямоугольников (рис. 3).

(5)

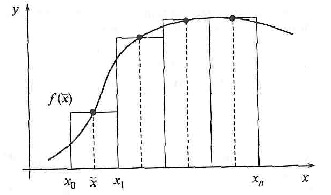
Рис. 3. Метод средних прямоугольников

Алгоритм вычисления интеграла по формуле левых прямо­угольников показан на рис. 4.

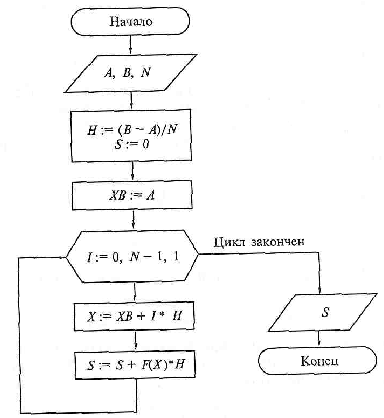
Рис. 4. Схема алгоритма вычисления интеграла

Пример 1. С помощью метода левых и правых прямо­угольников вычислить определенный интеграл

, полагая п = 4.

Решение

Зная пределы интегрирования, а = 1 и b = 9, находим шаг

Тогда точками разбиения будут

Значения подынтегральной функции в этих точках таковы:

y₀ = f(x₀) = ; y₁=f(x₁) = ; y₂ = ; y₃ = ; y₄ = .

Найдем численное значение интеграла по формуле левых прямоугольников:

По формуле правых прямоугольников:

Пример 2. Вычислить по методу левых прямоугольников:

Программа_________________________________________________

program integral 1;{Метод левых прямоугольников}

uses crt;

var i,n:integer;

a,b,h,x,xb,s:real;

function f(x:real):real;

begin

f:=(l/x)*sin(Pi*x/2);

end;

begin

clrscr; gotoxy(10,10);

textbackground(l); clrscr;

write(' Введите нижний предел интегрирования ');

readln(a); gotoxy(l0,12);

write('Введите верхний предел интегрирования ');

readln(b); gotoxy(10,14);

write('Введите количество отрезков '); readln(n);

h:=(b-a)/n; s:=0; xb:=a;

for i:=0 to n-1 do

begin

x:=xb+i*h; s:=s+f(x)*h;

end; gotoxy(10,18);

writeln ('Интеграл равен ',s: 12:10);

readkey;

end.

Пример 3. Вычислить по методу правых прямоугольников:

Программа_________________________________________________

program integral; {Метод правых прямоугольников}

uses crt;

var i,n:integer;

a,b,h,x,xb,s:real;

function f(x:real):real;

begin

f:=(l/x)*sin(3.14*x/2);

end;

begin

clrscr; gotoxy(10,10);

textbackground(l); clrscr;

write('Введите нижний предел интегрирования ');

readln(a); gotoxy(10,12);

write('Введите верхний предел интегрирования ');

readln(b); gotoxy(10,14);

write('Введите количество отрезков '); readln(n);

h:=(b-a)/n; s:=0;

xb:=a; for i:=l to n do

begin

x:=xb+i*h; s:=s+f(x)*h;

end;

gotoxy(10,18);

writeln('Интеграл равен ',s: 12:10);

readkey;

end.

Пример 4. Вычислить по методу средних прямоугольников:

Программа_________________________________________________

program integral; {Метод средних прямоугольников}

uses crt;

var i, n: integer;

a, b, dx, x, s, xb : real;

function f(x : real):real;

begin

f:=(l/x)*sin(3.14*x/2);

end;

begin

clrscr; gotoxy(10,10);

textbackground(l); clrscr;

write('Введите нижний предел интегрирования ');

readln(a); gotoxy(10,12);

write('Введите верхний предел интегрирования ');

readln(b); gotoxy(10,14);

write('Введите количество отрезков '); readln(n);

dx:=(b-a)/n; xb:=a+dx/2; s:=0;

for i:=0 to n-1 do

begin

x:=xb+i*dx; s:=s+f(x)*dx;

end;

gotoxy(10,18);

write('Интеграл равен ',s:15:10);

readkey;

end.