Интерполяционный многочлен Ньютона

Интерполяционным многочленом Ньютона называется многочлен

P(x) = y₀+(x-x₀)f(x₀,x_l) + (x-x₀)(x-x₁)f(x₀,x_l,x₂)+... + (x-x₀)(x-x_l)...(x-x_n-1)f(x₀,x_l,...,x_n), (11)

в котором f(x₀,x₁),f(x₀,x₁,x₂),...,f(x₀,x_l,...,x_n) – разделенные разности различных порядков. Этот многочлен удовлетворяет услови­ям y_k =f(x_k) = P_n(x_k) (к = 0,1,2,...,п).

Интерполяционной формулой Ньютона называется формула

f(x) y₀+(x-x₀)f(x₀,x_l)+(x-x₀)(x-x_l)f(x₀,x₁,x₂)+..+(x-x₀)(x-x_l)...(x-x_n-1)f(x_0,x₁,x₂,...,x_n). (12)

Замечание 1. Поскольку любой к-й член многочлена Ньютона зави­сит только от к первых узлов интерполяции и от значений функции в этих уз­лах, добавление новых узлов вызывает в формуле (11) лишь добавление новых членов без изменения первоначальных. Это является существенным преимуществом многочлена Ньютона по сравнению с многочленом Лагранжа.

Замечание 2. В силу единственности интерполяционного многочле­на n-ой степени интерполяционный многочлен Ньютона перегруппировкой членов можно преобразовать в интерполяционный многочлен Лагранжа и об­ратно.

В случае равноотстоящих узлов интерполяции (х₁ = x₀+h, x₂ = х₀ + 2h,...,х_п = х₀ + nh) из формулы (12) с учетом равенств (8) — (10) получается интерполяционная формула Ньютона для «интерполирования вперед»:

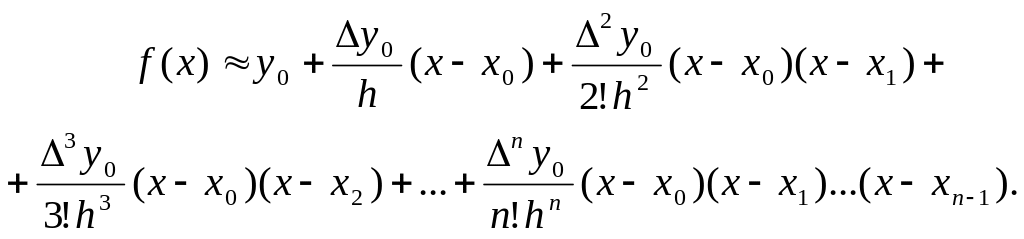(13)

Эта формула удобна при интерполировании функций для значений х, близких к наименьшему узлу х₀.

Интерполяционная формула Ньютона для «интерполирования на­зад» имеет вид:

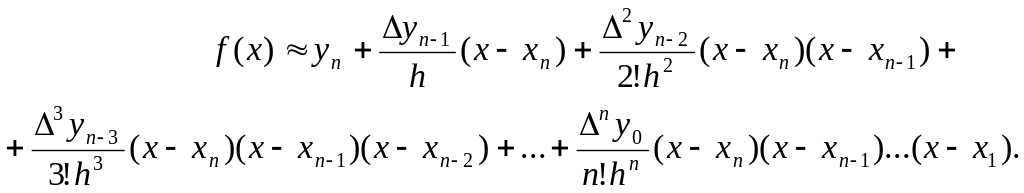(14)

Формула (14) удобна при интерполировании функций для значений х, близких к наибольшему узлу х_п.

Замечание. В формуле (13) коэффициенты многочлена содержат конечные разности различных порядков, принадлежащей верхней (нисходящей) строке таблицы разностей (см. таблицу 1). В формуле (14) коэффициенты многочлена содержат разности различных порядков, принад­лежащие нижней (восходящей) строке этой таблицы.

Пример 9 . Найти интерполяционный многочлен Ньютона для функции y = f(x), если известны ее значения:

f(2) = 1, f(4) = 15, f(5) = 28.

Решение

В данном случае

х₀ = 2, х₁ =4, х₂ = 5, y₀ = 1, y₁ = 15, у₂ = 28.

Отметим, что узлы не являются равноотстоя­щими (так как х₁ – х₀ х₂ – х₁). Интерполяционный многочлен (11) при n = 2 принимает вид

Р2(х) = у₀+(х-х₀)f(х₁,х₀) + (х-х₀)(х-х₁)f(х₂,х₁,х₀). (I)

Вычислим разделенные разности:

Подставив эти значения в формулу (I), найдем искомый интерпо­ляционный многочлен Ньютона:

Р₂(х)=1 + 7(х-2) + 2(х-2)(х-4).

Замечание. Раскрыв скобки и приведя подобные члены, получим Р₂(х) = 2х²-5х + 3.

Пример 10. Найти многочлены Ньютона «интерполирования впе­ред» и «интерполирования назад» для функции, заданной таблицей

x	0	1	2	3
y	5	1	7	29

Вычислить значения функции при х = 0,5 и х = 2,5.

Решение

В данном случае

х₀ =0, х₁ = 1, х₂ = 2, х₃ = 3; у₀ =5, у₁ = 1, у₂ = 7, у₃ = 29; узлы интерполирования являются равноотстоящими

(x₁ – x₀ = x₂ – x₁ =x₃ –x₂ = 1).

Составим таблицу конечных разностей различных порядков (таблица 3).

x	у	у	2у	3у
0 1 2 3	5 1 7	-4 6	10	6

Числа верхней (нисходящей) строки этой таблицы (подчеркнуты одной чертой) входят множителями в коэффициенты многочлена Нью­тона для формулы «интерполирования вперед». Правая часть формулы (13) при п=3 принимает вид

Использовав условие задачи и указанные числа, найдем многочлен Ньютона для «интерполирования вперед»

Р_в(х) = 5 - 4х + 5х (х - 1) + х(х - 1) (х - 2). (II)

Числа нижней (восходящей) строки таблицы 3 (подчеркнуты двумя чертами, включая и число 6) входят в коэффициенты многочле­на Ньютона для «интерполирования назад». Правая часть формулы (14) при n = 3 имеет вид

Использовав условие задачи и числа таблицы 3, подчеркнутые двумя чертами (включая число 6), найдем многочлен Ньютона для «интерполирования назад»

Р_н(х) = 29 + 22(х-3) + 8(х-3)(х-2) + (х-3)(х-2)(х-1). (III)

Значение функции при х = 0,5 найдем с помощью первого много­члена:

f(0,5) = Р_в(0,5)= 5 - 4_; 0,5 + 5- 0,5 (-0,5) + 0,5 (-0,5) (-1,5) = 2,125,

а значение функции при х = 2,5 - с помощью второго многочлена:

f(2,5) = Р_н (2,5) = 29 + 22 (- 0,5) + 8 (- 0,5) (0,5) + (- 0,5) • 0,5 • (1,5) = 15,625.

Замечание. Найденные многочлены отличаются только формой. Рас­крывая скобки и приводя подобные члены, получаем один и тот же многочлен в обычной форме:

Р₃(х) = х³ +2х² -7х + 5.