Разности различных порядков. Разделенные разности

Рассмотрим значения у_i = f(x_i) функции y = f(x) в точках х_i (i = 0,1,2,...): y₀=f(x₀), y₁ = f(x₁) у₂ = f(x₂),... Выделим все­возможные пары соседних значений: (уо,y₁), (y₁,y₂), (y₂, y₃),… и в каждом случае вычтем предыдущее значение из последующего, полу­чим разности: у₁ -у₀, y₂ – y₁, y₃ – y₂,…. Эти разности называются конечными разностями первого порядка или просто первыми разно­стями. Обозначения первых разностей:

(1)

или

Замечание. Иногда употребляются и другие обозначения, например,

Разностями второго порядка, или вторыми разностями, называют разности первых разностей и обозначают через :

(2)

Разности третьего порядка, или третьи разности, определяются и обозначаются так:

³y₀= ²y₁ - ²y₀, ³у₁ = ²у₂- ²у₁, …, ³у_n = ²у_n+1 - ²у_n, ...

Аналогично определяются последующие разности. Разности (к+1) -го порядка получаются из разностей к -го порядка по форму­лам

,... (3)

Таблица разностей различных порядков строится согласно схеме (таблица 1).

Таблица 1

x	y	y	2y	3y	4y	5y
x0 x1 x2 x3 x4 x5	y0 y1 y2 y3 y4 y5	y0 y1 y2 y3 y4	2y0 2 y1 2 y2 2 y3	3y0 3 y1 3 y2	4y0 4 y1	5y0

Каждое число этой таблицы (начиная с третьего столбца) является разностью двух смежных чисел столбца слева (из нижнего числа вычи­тается верхнее; разность записывается в следующем столбце между этими числами). Третий столбец содержит первые разности, четвер­тый - вторые и т. д.

Для контроля вычислений при составлении таблицы разностей пользуются следующим утверждением: сумма чисел в каждом столбце разностей равна разности крайних чисел предыдущего столбца. На­пример, у₀ + у₁ + у₂+...+ y_n-1 + у_n =(y₁ - у₀) + (у₂ – y₁) + (у₃ -у₂)+…+(у_n – у_n-1) + (у_n+1 – у_n) = у_n+1 – y₀.

Все разности в таблице принято записывать целыми числами или в единицах младшего разряда значений функции.

Замечание. Конечные разности п-ro порядка от многочлена степени п постоянны, а конечные разности (n+1)-го порядка равны нулю. Это свой­ство дает простой способ составления таблиц многочленов. Непосредственно вычисляем значения многочлена для п +1 значений аргумента и составляем таблицу, в которую входят разности до п-ro порядка включительно. Далее, пользуясь тем, что разности п-го порядка постоянны, продолжаем столбец разностей (п–1) -го порядка. Для получения новых чисел этого столбца скла­дываем соответствующие разности (n-1)-го порядка с разностями п-го по­рядка. Затем последовательно продолжаем столбцы разностей (п – 2) -го, (п – 3) -го порядков и т. д. пока не получим продолжение столбца у_i = f(x_i), т. е. значений многочлена.

Разделенные разности первого порядка определяются формулами

(4)

Разделенные разности второго порядка получаются из разделенных разностей первого порядка по формулам

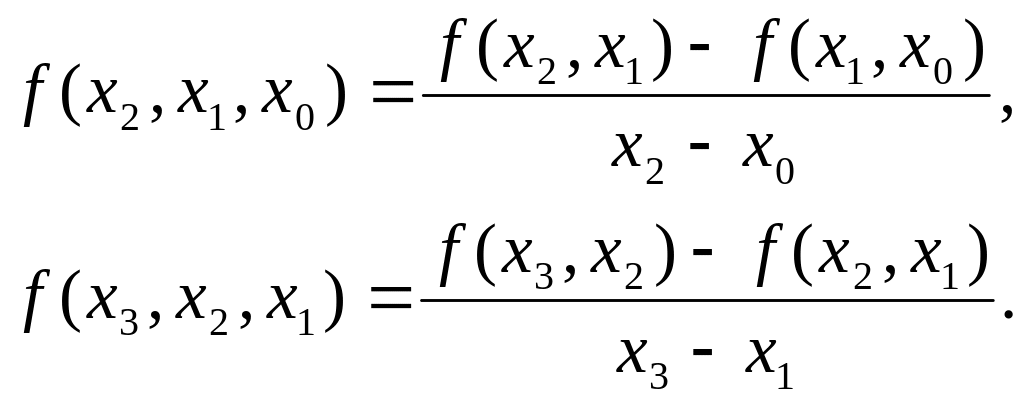(5)

Аналогично определяются разделенные разности третьего порядка:

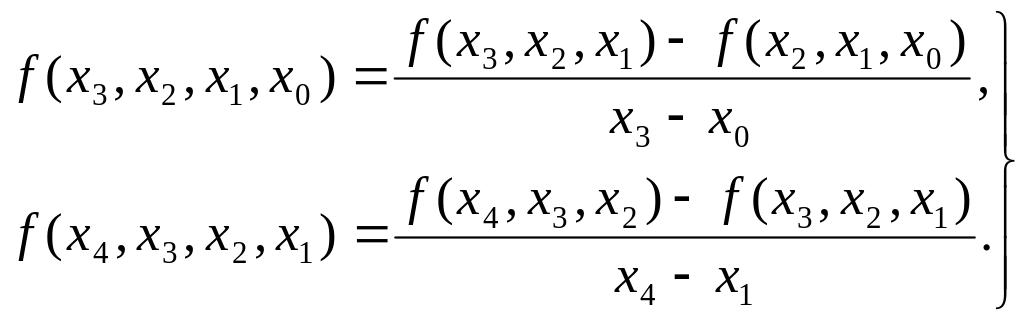(6)

Разделенные разности n-го порядка получаются из разностей (n-1) -го порядка по формулам

(7)

В случае равноотстоящих узлов с шагом h (х_k = х₀ + kh) разде­ленные разности различных порядков имеют вид:

(8)

(9)

(10)

Пример 8. Составить таблицу разностей различных порядков при следующих значениях х и f(х):

x₀ = -1, х₁ = -2, x₂ = 1, х₃ = 2, х₄ = 3;

y₀ = 0, у₁ =1, у₂ =30, у₃ = -16, y₄ = -45.

Решение

По формулам (1) находим первые разности:

y₀ = у₁ - уо = 7 - 0 = 7; y₁ = у₂ - y₁ = 30 -7 = 23;

y₂ = y₃ – y₂ = -16 - 30 = -46; у₃ = у₄ - у₃ = -45 - (-16) = -29.

В соответствии с формулами (2) вычисляем разности второю порядка:

²у₀ = у₁ - у₀ = 23 - 7 = 16; ²у₁ = у₂ - y₁ = -46 - 23 = -69;

²у₂ = у₃ - y₂ = -29 - (-46) = 17.

Пользуясь определениями и соответствующими формулами полу­чаем разности третьего порядка:

³у₀ = ²у₁ - ²у₀ = -69 -16 = -85;

³ у₁ = ²у₂ - ²у₁ =17 -(-69) = 86

и разность четвертого порядка ⁴у₀ = ³y₁ - ³y₀ = 86 - (-85) = 171.

Полученные разности можно представить в виде таблицы 2.

Таблица 2

x	у	у	2у	3у	4у
-1 -2 1 2 3	0 7 30 -16 -45	7 23 -46 -29	16 -69 17	-85 86	171
		-45	-36	1
S	-45	-36	1

Замечание. Последние две строки служат для контроля вычислений: в строке числа равны суммам чисел, стоящих в соответствующем столб­це, в строке S -разности последнего и первого чисел соответствующего столбца. Совпадение этих чисел (по диагонали) означает, что вычисления сде­ланы верно.