Интерполяционный многочлен Лагранжа

Пусть функция y=f(x) задана таблицей. Построим интерполяционный многочлен L_n(x), степень которого не больше n и выполняются условия: L_n(x) =у_i i = 0, 1, ..., п. Будем искать L_n(x) в виде

L_n(x) = р₀(х)у₀ + р₁(х)у₁ + ... + рп(х)у_п = р_i(х)у_i,

где р_i(х) — многочлен степени п;

, т. е. р_i(х) только в одной точке отличен от нуля при i=j, а в остальных точках он обращается в нуль. Сле­довательно, все эти точки являются для него корнями:

p_i(x) = с(х - х₀)(х – х₁)...(х – х_i-1)(х – х_i+1)...(х – х_n);

При x = x_i

p_i(x_i) = с(x_i – x₀)(х_i – x₁)...(х_i – х_i-1)(х_i – х_i+1)...(х_i – х_n);

с = [(x_i - х₀)(х_i – х_i)...(х_i – х_i-1)(х_i – х_i+1)...(х_i – х_n)]^-1;

подставим с в формулу p_i(x), получим:

отсюда

Это и есть интерполяционный многочлен Лагранжа. По не­полной таблице формула позволяет весьма просто составить внешний вид многочлена.

Пример 1. Построить интерполяционный многочлен Лагранжа для функции, заданной таблично

X	1	2	3	5
Y	1	5	14	81

Решение

Степень L_n(x) не выше третьей, так как функция задается четырьмя значениями:

Пример 2. Для функции у = sin( x) построить интерполяционный полином Лагранжа, выбрав узлы х₀ = 0; x₁ = ; х₂ =

Решение

Вычислим соответствующие значения функции:

у₀ = 0;

Применяя формулу, получаем

Пример 3. Построить интерполяционный полином Лагранжа для двух узлов интерполяции:

x	x0	x1
y	y0	y1

x	1	3
y	1	9

Решение

N= 0, 1 (два узла интерполяции).

— уравнение прямой, проходящей через точки (х₀, у₀), (х₁, у₁);

Пример 4. Построить интерполяционный полином Лагранжа для трех узлов интерполяции:

x	1	3	4
y	12	4	6

x	x0	x1	x2
y	y0	y1	y2

Решение

N= 0, 1, 2 (три узла интерполяции).

- уравнение параболы, проходящей через точки (x₀, y₀), (x₁, y₁), (x₂, y₂);

Построим график этой функции (рис. 1) и отметим на нем узловые точки М_i(х_i, у_i).

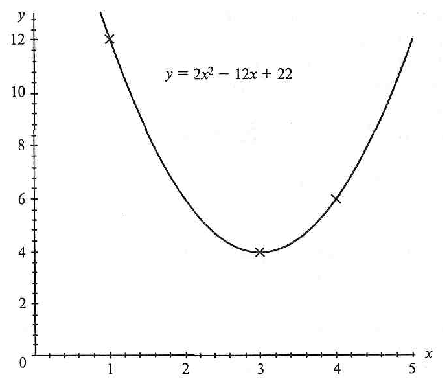
Рис 1. График полученной функции (к примеру 4)

Пример 5. Найти приближенное значение функции f(arg) при данном значении аргумента arg с помощью интерполяционного многочлена Лагранжа, если функция задана таблицей

x	x0	x1	...	xn
y	y0	y1	…	yn
arg=…

Программа________________________________________

program Lagrange;

uses Crt;

var X, Y : array[1.. 100] of Real;

Arg, L, F : Real;

I, J, N integer;

begin

Write('Введите количество узлов интерполяции');

Readln(n);

Writeln ('В ведите таблицу значений xi, yi');

for I:=0 to N do begin

Write('X[',I,']='); ReadLn(X[I]);

Write('Y[',I,']^); ReadLn(Y[I]);

end;

Write('Введите аргумент '); Readln(Arg);

L:=0;

For I:—0 to N do begin

F:=l;

for J:=0 to N do

if IOJ then F:=F*(Arg-X[J])/(X[I]-X[J]);

F:=F*Y[I]; L:=L+F;

end;

Writeln('Значение многочлена Лагранжа в точке ',Arg:0:3);

Writeln('Равно ', L:0:3);

Readln;

end.