Алгоритми переведення чисел з однієї позиційної системи числення в іншу

1. Для переведення чисел із системи числення з основою p в систему числення з основою q, використовуючи арифметику нової системи числення з основою q, потрібно записати коефіцієнти розкладу, основи степенів і показники степенів у системі з основою q і виконати всі дії в цій самій системі. Очевидно, що це правило зручне при переведенні до десяткової системи числення.

Наприклад:

з шістнадцяткової в десяткову:

92C8₁₆=9*10₁₆³+2*10₁₆²+C*10₁₆¹+8*10₁₆⁰= 9*16₁₀³+2*16₁₀²+12*16₁₀¹+8*16₁₀⁰=37576

з вісімкової в десяткову:

735₈=7*10₈²+3*10₈¹+5*10₈⁰= 7*8₁₀²+3*8₁₀¹+5*8₁₀⁰=477₁₀

з двійкової в десяткову:

110100101₂=1*10₂⁸+1*10₂⁷+ 0*10₂⁶+1*10₂⁵+0*10₂⁴+0*10₂³ + 1*10₂²+ 0*10₂¹ + 1*10₂⁰= 1*2₁₀⁸+1*2₁₀⁷ + 0*2₁₀⁶+1*2₁₀⁵+ 0*2₁₀⁴+ 0*2₁₀³+1*2₁₀²+0*2₁₀¹+ 1*2₁₀⁰=421₁₀

2. Для переведення чисел із системи числення з основою p в систему числення з основою q з використанням арифметики старої системи числення з основою p потрібно:

• для переведення цілої частини:

  • послідовно число, записане в системі основою p ділити на основу нової системи числення, виділяючи остачі. Останні записані у зворотному порядку, будуть утворювати число в новій системі числення;

• для переведення дробової частини:

  • послідовно дробову частину множити на основу нової системи числення, виділяючи цілі частини, які й будуть утворювати запис дробової частини числа в новій системі числення.

Цим самим правилом зручно користуватися в разі переведення з десяткової системи числення, тому що її арифметика для нас звичніша.

Приклади: 999,35₁₀=1111100111,01011₂

для цілої частини:

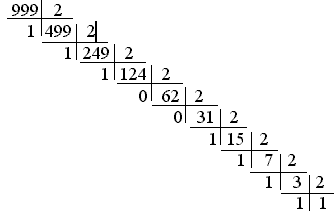
для дробової частини:

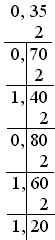
Арифметичні основи цифрових пристроїв. При виконанні різних операцій в сучасних цифрових пристроях і системах числа звичайно представляються в двійковій системі счислення. Це зв'язано з тим, що для представлення значення символів цифр двійкової системи счислення можна використовувати прості електронні схеми з двома електричними станами. Прийнято, що символ “1” представляється деяким стандартним рівнем напруги або струму, а “0” - нульовим або близьким до нуля рівнем напруги або струму.

  Арифметичні операції над двійковими числами можуть проводитися за тими ж правилами, що і над десятковими, проте, з метою спрощення цифрових систем для виконання арифметичних операцій застосовують алгоритми, відмінні від алгоритмів дій десяткової арифметики.

  В двійковій системі счислення для представлення знака числа використовується додатковий знаковий розряд (один або декілька розрядів), який розташовується перед старшим числовим розрядом. Для позитивних чисел значення знакового розряду Зн.р.=0, для негативного числа Зн.р.=1.

        Операція віднімання в цифрових системах реалізується за допомогою операції складання. Від'ємник при цьому представляється в додатковому коді (якщо розрахунок не вимагає високої точності - в зворотному коді).

        Двійковий код із знаком називають також прямим кодом. Як приклад розглянемо позитивне і негативне числа, десятковий еквівалент яких рівний 46_10.

0000000000101110 - код додатного числа

1111111111010010 – код від’ємного числа

Примітка: для запису додатних чисел дозволяється брати не повний запис, а лише значущі дані, тобто у нашому випадку дозволений запис у виді 101110

Зворотний код виходить шляхом заміни всіх “0” на “1” і всіх “1” на “0” прямого коду (двійкового числа із знаком).

                Заміна “0” на одиницю (“1”) називається інвертуванням (також і заміна “1” на “0”).

                Зворотний код, доповнений одиницею в молодшому розряді, називається додатковим кодом. Послідовність дій при отриманні додаткового коду:

 

0000000000101110 - прямий код

проводимо інвертування всіх розрядів

1111111111010001 – обернений код

+ 1 – додання 1 до молодшого розряду

________________

1111111111010010 додатковий код (запис від’ємного числа)

                Складання і віднімання двійкових чисел. Правила складання двох двійкових чисел можна показати на наступному прикладі:

0+0=0

0+1=1

1+0=1

1+1=10

              Приклад складання багаторозрядних чисел. Вимагається скласти два числа 1810 і 2310

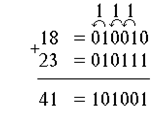
                Віднімання в цифрових пристроях проводиться також як і складання, тільки число, яке віднімаємо, представляється в додатковому коді. Розглянемо два приклади, в першому потрібен з числа 23 відняти число 18, а в другому  з 18 відняти 23. З початку число, яке віднімаємо, представимо в додатковому коді:

1111111111101110 – додатковий код числа -18

1111111111101001 – додатковий код числа -23

1)

23 = 0000000000010111

+

-18 = 1111111111101110

5 = 0000000000000101

 2)

18 = 0000000000010010

+

-23 = 1111111111101001

-5 = 1111111111111011

 

                Прийнято вважати, що додатковий код позитивного числа співпадає з його прямим кодом.

                Операція віднімання з використанням тільки зворотного коду (без додаткових операцій по перекладу його в додатковий код) приводить до помилки, визначуваною одиницею в молодшому розряді, і тому при точних розрахунках не застосовується.