Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Чувашский государственный университет им. И.Н. Ульянова»

Электротехнический факультет

Кафедра систем автоматического управления электроприводами

Реферат на тему:

Метод симметричных составляющих

Выполнил: студент ЭТ-41-11

Соловьев С.

Проверил: Калинин А.Г.

Чебоксары 2013

Содержание

1. Введение…………………………………………………………….. 2

2. Симметричные составляющие трехфазной системы величин..... ..2

3. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений..................................................... .4

4. Сопротивления симметричной трехфазной цепи для токов различных последовательностей...............................................................................5

5. Применение метода симметричных составляющих для симметричных цепей.........................................................................................................6

6.Список использованной литературы.................................................9

Введение

Для анализа и расчетов несимметричных режимов в трехфазных цепях широко применяется метод симметричных составляющих. Он основан на представлении любой трехфазной несимметричной системы величин (токов, напряжений, магнитных потоков) в виде суммы в общем случае трех симметричных систем величин. Эти симметричные системы, которые в совокупности образуют несимметричную систему величин, называются ее симметричными составляющими. Симметричные составляющие отличаются друг от друга порядком следо­вания фаз, т. е. порядком, в котором фазные величины проходят через мак­симум, и называются системами _Прямой, обратной и нулевой последовательностей.

Симметричные составляющие трехфазной системы величин

Обозначим трехфазную систему величин (токов, напряжений, магнитным потоков) для общности буквами А, В^: и С. Величины, относящиеся к системам прямой, обратной и нулевой последова­тельностей, отметим соответственно индексами 1, 2 и 0. На рис. 11.1 показав пример векторных диаграмм симмет­ричных составляющих всех трех последовательностей.

Система прямой последовательности имеет порядок следования фаз А, В, С. Система обратной последовательности имеет порядок следования фаз А, С. В Система нулевой последовательности состоит из трех одинаковых величин, совпадающих по фазе. Для этих трех систем можно записать

В₁= А₁ е^-j2π/3 ; C₁= А₁е^j2π/3 ; (11.1)

B₂= A₂ e ^j2π/3 ; C₂= A₂ e^-j2π/3 ; (11.2)

A₀=B₀=C₀ (11.3)

Комплексное число е^j2π/3 называется фазным множителем и сокра­щенно обозначается буквой а:

а= е^j2π/3= е^-j4π/3= cos(2π/3)+jsin(2π/3) = -1/2+j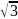 /2 (11.4)

Умножение вектора на a соответ­ствует повороту его против направле­ния движения часовой стрелки (вперед) на 120 или повороту по направлению движения часовой стрелки (назад) на 240°:

a²= е^j2π/3* е^j2π/3= е^j4π/3= e^-j2π/3=-1/2-j /2 (11.5)

Умножение вектора на a² соответ­ствует повороту его вперед на 240° или повороту назад на 120°.

При помощи фазного множителя выражения (11.1) и (11.2) можно записать так:

В₁=a² A₁ ; C₁=a A₁; (11.6)

B₂=a A₂ ; C₂= a²A₂ ; (11.7)

Кроме того а³= е^2jπ = 1 (11.8)

Пользуясь соотношением (11.8), мож­но исключать из формул множитель а в степени выше второй:

а⁴ = а³ а = а; а⁵ = а ³а² = а² и т. д.

Как следует из (11.4) и (11.5), 1, а и а² образуют симметричную систему единичных векторов (рис. 11.2).

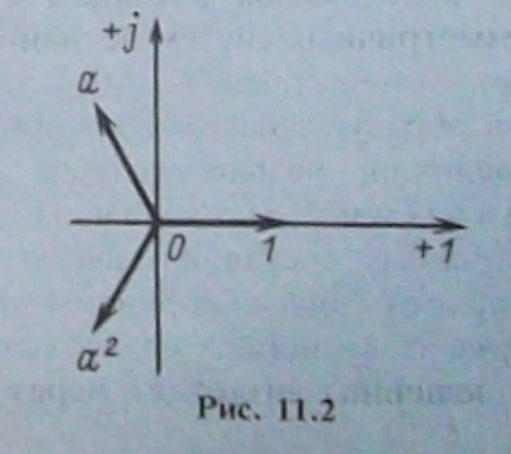
Их сумма 1+а+а²=0 (11.9)

Докажем теперь, что любую несим­метричную систему векторов А, В и С можно разложить на симметричные системы прямой, обратной и нулевой последовательностей. Если это имеет место, то

A = A₁ + A₂ + A₀ ; (11.10)

B = B₁ + B₂+ B₀ ; (11.11)

C = C₁ + C₂ + C₀ ; (11.12)

Выразим в этих предполагаемых ра­венствах все векторы симметричных си­стем через векторы A₁, A₂, и А₀, поль­зуясь соотношениями (11.3), (11.6) и (11.7):

A = A₁ + A₂ + A₀ ; (11.13)

B = а²А₁ + аА₂ + А₀ ; (11.14)

C = a A₁ + а² А₂ + А₀ ; (11.15)

Получены три уравнения, из кото­рых однозначно можно определить век­торы A₁, A₂, и А₀ , что и доказывает возможность разложения заданной не­симметричной системы векторов А, В и С на три симметричные системы.

После сложения уравнений (11.13)— (11.15) получим

А + В + С = (1+ а+а²)А₁ + (1+а+а²) A₂ + 3 A_0. Откуда с учетом (11.9) найдем, что

А₀ = 1/3(A + B + C). (11.16)

Умножая (11.14) на а и (11.15) на а² и затем складывая уравнения (11.13) - (11.15), находим , что

A₁=1/3(A + аB + а² C) (11.17)

Умножая (14.14) на а² и (11.15) на а и затем складывая уравнения (11.13) - (11.15), получаем A₂=1/3(A + а²В + а C) (11.18)