РАЗВЕРТКИ ПОВЕРХНОСТЕЙ.
http://library.uipa.kharkov.ua/library/BD/VidannaKaf/5/5/NGP/5.htm
Развернуть поверхность - это значит, совместить ее с плоскостью без складок и разрывов. При этом длины линий, величины углов и площадей, взятых на поверхности, должны быть равны таким же элементам, взятым на плоскости. Поверхности, допускающие такие преобразования, называют развертывающимися. К ним относятся все гранные поверхности, а также линейчатые поверхности с одной направляющей - торсы, конические и цилиндрические поверхности. Остальные поверхности относятся к неразвертывающимся.
Основным способом построения разверток гранных поверхностей является способ триангуляции или, как еще его называют, способ треугольников. Его суть сводится к следующему. Все грани заданной поверхности с помощью диагоналей разбивают на треугольники. Определяют истинные величины сторон каждого из них, а затем линейными засечками строят на плоскости систему истинных величин сомкнутых треугольников, не нарушая их взаимного положения.
Пример 78. Построить развертку трехгранной усеченной пирамиды (рис.302).
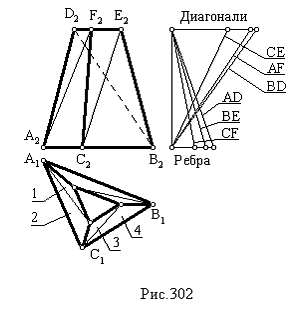
Верхнее и нижнее основания пирамиды параллельны горизонтальной плоскости проекций P1, поэтому истинные величины сторон треугольников, лежащих в этих основаниях, равны их горизонтальным проекциям.
Боковые грани пирамиды представляют собой четырехугольники ADFC, CFEB, BEDA. С помощью диагоналей AF, CE, BD разбиваем каждый из них на два треугольника. В итоге получаем шесть треугольников.
Определяем истинные величины сторон каждого из них. Боковые ребра пирамиды и диагонали граней являются отрезками общего положения. Их истинные величины целесообразно определять способом прямоугольного треугольника. Для этого достаточно построить прямоугольные треугольники, одним катетом которых будет, например, горизонтальная проекция отрезка, а другим - разность высот его концов. Поскольку таких треугольников должно быть шесть, то это приведет к накоплению значительного количества неупорядоченных линий на горизонтальной проекции пирамиды, что будет усложнять дальнейшую работу. Поэтому естественным является стремление вынести построение этих треугольников за границы горизонтальной проекции пирамиды и упорядочить. Это возможно, так как одним из их катетов является одна и та же величина - разность высот концов ребер и диагоналей, равная высоте пирамиды. Поэтому примем этот катет общим для всех треугольников. Отложим его параллельно высоте пирамиды рядом с ее фронтальной проекцией, а перпендикулярно к нему - горизонтальные проекции ребер и диагоналей (для большего удобства работы горизонтальные проекции ребер будем откладывать с одной стороны, а диагоналей – с другой). Полученный чертеж называют диаграммой истинных величин.
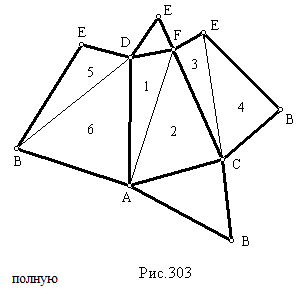
Проведем произвольную прямую (рис.303) и отложим на ней истинную величину какого-либо ребра, например BE. Чтобы получить треугольник BED, необходимо построить точку D. Для этого из точки E проведем дугу окружности радиусом, равным истинной величине стороны ED, а из точки B – радиусом, равным истинной величине диагонали BD. На пересечении этих дуг и будет находиться точка D. Соединив ее с точками B и E, получим истинную величину треугольника BED. Сделав засечки из точек B и D истинными величинами соответственно сторон BA нижнего основания и ребра DA, получим точку A и, следовательно, треугольник BDA. Продолжив построение треугольников, получим полную развертку пирамиды.
Способ триангуляции носит общий характер и может использоваться для построения развертки любой гранной поверхности. Однако развертку призматических поверхностей целесообразней строить способом нормального сечения. Его суть состоит в построении истинной величины граней призмы без их разбиения на треугольники.
Пример 79. Построить развертку трехгранной призмы (рис.304).
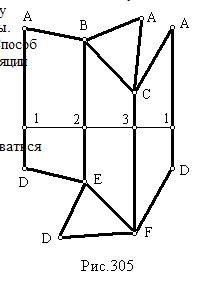
Пересечем призму произвольной горизонтально проецирующей плоскостью S перпендикулярно ребрам и способом замены плоскостей проекций определим истинную величину сечения. Выберем произвольную горизонтальную линию (рис.305) и последовательно от произвольно выбранной точки 1 отложим отрезки 12, 23, 31, равные по величине соответственно сторонам треугольника сечения призмы 1424, 2434, 3414. Через точки 1, 2, 3, 1 проведем прямые, перпендикулярные этой линии, и отложим на них от точек 1, 2, 3, 1 отрезки, равные отрезкам боковых ребер призмы (поскольку ребра призмы являются отрезками уровня, то их горизонтальные проекции равны истинной длине ребер), и полученные точки соединим отрезками прямых. К полученной развертке боковой поверхности призмы способом линейных засечек достраиваем истинные величины треугольников верхнего и нижнего оснований.
Построение разверток кривых развертывающихся поверхностей, как правило, связано со значительными техническими трудностями. Поэтому обычно ограничиваются построением их приближенных разверток. Для этого в заданную кривую поверхность вписывают гранную поверхность и строят ее развертку. Эту развертку и принимают за развертку кривой поверхности. При этом точность приближенной развертки кривой поверхности определяется тем, насколько точно вписанный многогранник аппроксимирует кривую поверхность.