Производится наблюдение за группой, состоящей из четырех однородных объектов. Каждый из них, за время наблюдений, может быть обнаружен или не обнаружен. Рассматриваются события: А – обнаружен ровно один из четырех объектов; В – обнаружен хотя бы один объект: С – обнаружено не менее двух объектов; D – обнаружены все четыре объекта. В чем состоят события: а)
,
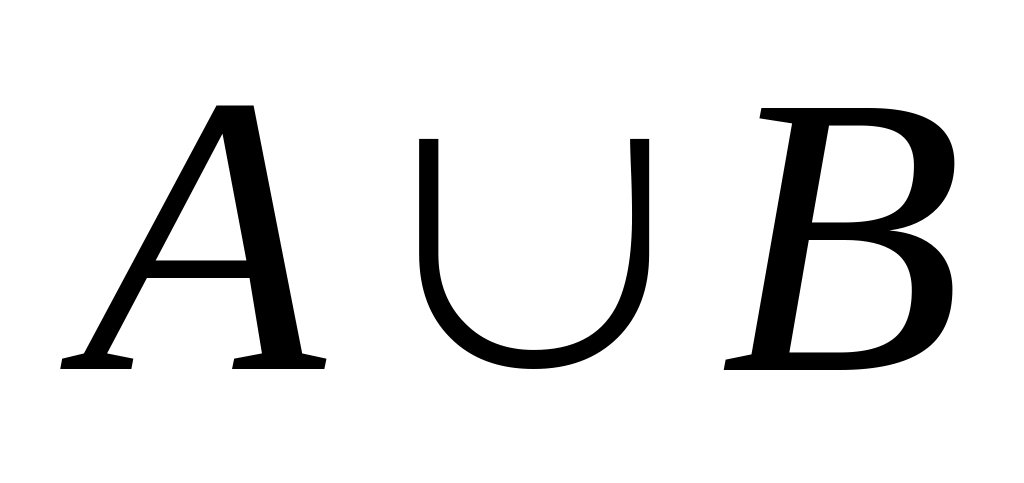б)
,
в) ВС,
г) совпадают ли события BD
и С?Из урны, содержащей три белых, два черных и пять красных шаров, наудачу без возвращения извлекают три шара. Найти вероятность обнаружить среди них один черный и два белых.
Прибор может работать в двух режимах: нормальном и форсированном. Нормальный режим наблюдается в 90% случаев работы приборов. Вероятность выхода прибора из строя при нормальном режиме равна 0,08, а при форсированном - 0,8. Во время работы прибор вышел из строя. В каком режиме это вероятнее всего случилось?
В розыгрыше первенства по футболу участвует 18 команд, из которых случайным образом формируются две группы по 9 команд. Среди участников соревнований имеется 5 команд экстра класса. Найти вероятность того, что все команды экстра класса попадут в одну и ту же группу.
Стрелок ведет стрельбу до первого попадания, имея боезапас 4 патрона. Вероятность попадания при каждом выстреле равна 0,6. Составить закон распределения числа израсходованных патронов. Найти М(Х), D(X), σ(X) и F(X), где Х -число израсходованных патронов.
Дана функция распределения
случайной величины Х.
Найти: а) плотность распределения f(X);
б) построить графики F(X)
и f(X);
в) в) М(Х);
г) D(X);
д) σ(X);
е)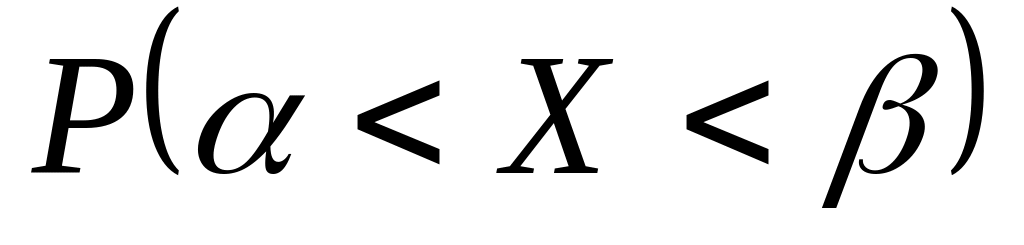
.Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 14
По мишени производится три выстрела. Рассматриваются события Аi – попадание при i-м выстреле (i = 1, 2, 3). В алгебре событий выразить следующие события: А – все три промаха; В – хотя бы одно попадание; С – не меньше двух попаданий; Д – попадание в мишень не раньше, чем в третьем выстреле.
Буквенный замок содержит на общей оси 4 диска, каждый из которых разделен на 5 секторов, отмеченных идущими подряд натуральными числами. Замок открывается только в том случае, когда цифры образуют соответствующую комбинацию. Найти вероятность открыть замок, установив произвольную комбинацию цифр. Какова вероятность открыть замок, если известно, что кодовая комбинация содержит цифры 1, 2, 3, 5 и цифры не повторяются?
Вор знает, что квартира оборудована одним из трех типов сигнализации. Они срабатывают с вероятностью 0,5, 0,8, 0,9. Какова вероятность того, что при взломе сигнализация сработает, если вероятности того, что квартира оборудована i-м типом сигнализации, равны.
В скачках участвуют три лошади. Первая лошадь приходит первой с вероятностью 0,6, вторая – с вероятностью 0,4, а третья – 0,5. 30% зрителей на ипподроме ставят на первую лошадь, 18% - на вторую, остальные – на третью. Ваш случайный знакомый выиграл. На какую лошадь он вероятнее всего делал ставку?
Монета бросается 5 раз. Составить закон распределения числа появлений гербов. Найти М(Х), D(X), σ(X) и F(X) числа появлений гербов.
Дана функция распределения случайной величины Х.
Найти: а) плотность распределения f(X); б) построить графики F(X) и f(X); в) в) М(Х); г) D(X); д) σ(X); е) .
Дана плотность распределения
непрерывной случайной величины Х. Найти: а) параметр а; б) функцию распределения F(X).
Вариант 15
Пусть событие Г – появление герба в i-м бросании монеты, Р – появление решки в i-м бросании монеты. Монету подбрасывают два раза. Постройте множество элементарных исходов и выявите состав подмножеств, соответствующих событиям: А – выпало два герба; В – выпал герб и решка; С – в первом бросании выпал герб, во втором бросании герб не выпал; Д – не разу не выпал герб.
На сортировочном пункте в ожидании подачи на подъездной путь стоят 6 вагонов для различных пунктов. Определить вероятность того, что вагоны стоят в нужном для подачи порядке. Найти вероятность того, что первые два вагона стоят в нужном для подачи порядке.
В группе из 25 студентов есть три человека, которые занимаются боксом, 10 человек – футболом, 5 – спортивной гимнастикой, остальные 7 человек посещают только уроки физкультуры. Какова вероятность того, что среди трех наудачу выбранных студентов есть хотя бы один, занимающийся гимнастикой. Какова вероятность того, что среди наудачу выбранных трех студентов один занимается боксом, другие два футболом?
Патроны у охотников снабжены капсюлями трех типов. Причем 40% патронов снабжены капсюлями первого типа, 50% - второго и 10% - третьего типа. Капсюли первого типа дают осечку с вероятностью 0,1, второго - с вероятностью 0,15, третьего - с вероятностью 0,2. Охотник зарядил ружье патронами взятыми наудачу. Оно дало осечку. Какова вероятность, что в патроне был капсюль первого типа ?
При штамповке математических клемм получается в среднем 99% годных. В выпущена партия из 900 клемм. Найти закон распределения числа негодных клемм. Найти М(Х), D(X), σ(X) и F(X) этой случайной величины.
Дана функция распределения случайной величины Х.
Найти: а) плотность распределения f(X); б) построить графики F(X) и f(X); в) в) М(Х); г) D(X); д) σ(X); е) .