
- •Задания контрольной работы №4 Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Дана функция распределения f(X) случайной величины X. Найти: а) плотность распределения f (X); б) построить графики функций f(X) и f(X); в) м(х); г) d(X); д) σ(X); е) .
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 8
- •Вариант 9
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X).
- •Вариант 10
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 11
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 12
- •Вариант 13
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 14
- •Вариант 15
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 16
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 17
- •Вариант 18
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 19
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 20
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 21
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 22
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 23
- •Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 24
- •Вариант 25
- •Дана функция распределения f(х) случайной величины х.
Эксперимент состоит в бросании игральной кости. Пусть событие А – появление трех очков, событие В – появление нечетного числа очков, событие С – появление не больше пяти очков. Постройте множество элементарных исходов и выявите состав подмножеств, соответствующих событиям: а) ; б)
 ;
в)
.
;
в)
.Жюри состоит из трех судей. Первый и второй судьи принимают правильное решение независимо друг от друга с вероятностью 0,8, а третий судья для принятия решения бросает монету. Окончательное решение принимается по большинству голосов. Какова вероятность того, что жюри примет правильное решение?
На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 0,2% брака, второй – 0,4% и третий – 0,1%. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000 деталей, со второго – 2500 и с третьего – 3000 деталей.
Для сигнализации об аварии используются два вида сигнализаторов А-1 и А-2, каждый из которых срабатывает с вероятностями, равными соответственно 0,8 и 0,9. Вероятность того, что устройство снабжено одним из этих сигнализаторов, равна соответственно 0,6 и 0,4. Получен сигнал об аварии. Вероятнее всего, сигнализатором какого типа было снабжено устройство?
Составить закон распределения числа попаданий в цель, если произведено 5 выстрелов, а вероятность попадания при одном выстреле равна 0,3. Найти М(Х), D(X), σ(X) и F(X), где X – число попаданий в цель.
Дана функция распределения f(X) случайной величины X. Найти: а) плотность распределения f (X); б) построить графики функций f(X) и f(X); в) м(х); г) d(X); д) σ(X); е) .
![]()
Дана плотность распределения f(X) =
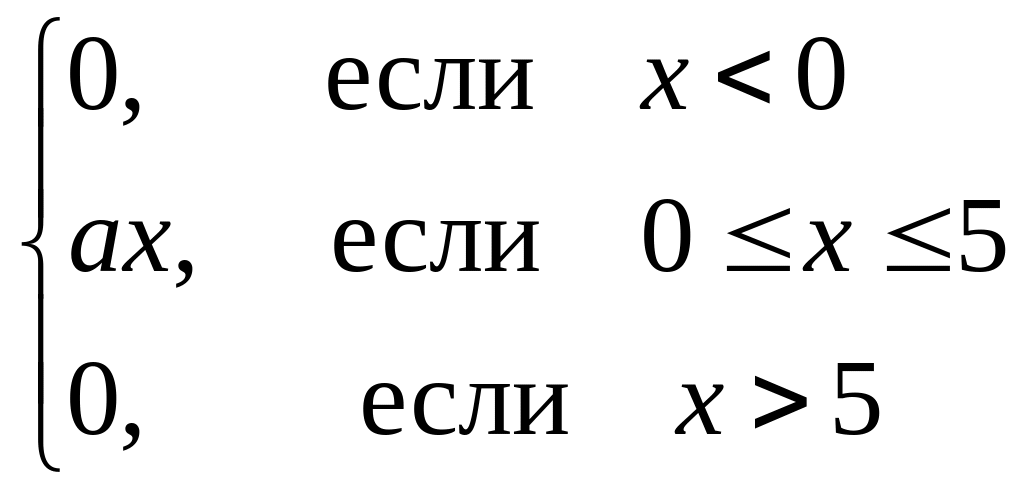 непрерывной случайной величины Х.
Найти: а) параметр а;
б) функцию распределения F(X).
непрерывной случайной величины Х.
Найти: а) параметр а;
б) функцию распределения F(X).
Вариант 5
Эксперимент состоит в бросании игральной кости. Пусть событие А – появление нечетного числа очков, В – не появление трех очков, С – не появление пяти очков. Постройте множество элементарных исходов и выявите состав подмножеств, соответствующих событиям: а) АВС; б) ;
в)
![]() .
.
Три оператора радиолокационной установки производят соответственно 20%, 35%, 45% всех измерений допуская ошибку с вероятностью 0,1, 0,08, 0,15. Найти вероятность того, что случайно выбранное измерение будет ошибочным.
В городе распространяются только билеты лотерей «Лото лимон», «Лото апельсин», «Лото мандарин». Среди горожан, которые приобрели билеты, 25% отдали предпочтение «Лото лимон», 40% - «Лото апельсин», остальные – «Лото мандарин». Билеты «Лимона» выигрывают с вероятностью 0,2, «Апельсина» - с вероятностью 0,15, «Мандарина» - 0,25. По телевидению был показан счастливчик, выигравший в одну из лотерей. Вероятнее всего, билеты какого «Лото» он купил?
Рабочий обслуживает 4 однотипных станка. Вероятность того, что в течение часа станок потребует регулировки, равна 1/3. Какова вероятность того, что в течение часа рабочему придется регулировать не более одного станка?
Вероятность приема сигнала равна 0,8. Сигнал передается 5 раз. Составить закон распределения числа передач, в которых сигнал будет принят. Найти М(Х), D(X), σ(X) и F(X), где X – число передач, в которых сигнал будет принят.
Дана функция распределения случайной величины X.
![]()
Найти: а) плотность распределения f(X); б) построить графики F(X) и f(X); в) М(Х); г) D(X); д) σ(X); е) .
Дана плотность распределения f (X) =
 непрерывной случайной величины Х.
Найти: а) параметр а;
б) функцию распределения F(X).
непрерывной случайной величины Х.
Найти: а) параметр а;
б) функцию распределения F(X).
Вариант 6
Электронная система содержит 3 транзистора, 4 конденсатора и 5 резисторов. Событие
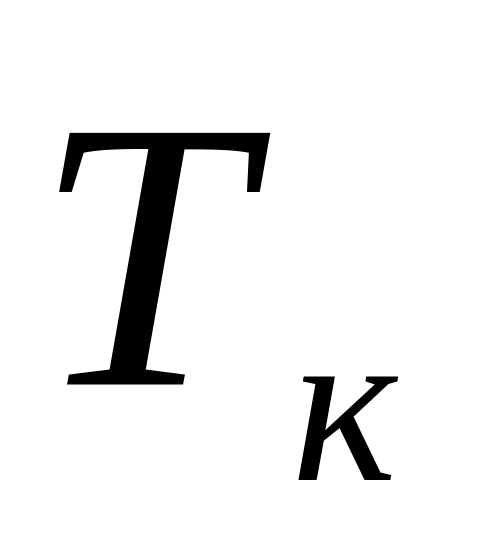 - выход из строя к-го
транзистора (к
= 1, 2, 3), событие
- выход из строя к-го
транзистора (к
= 1, 2, 3), событие
 - выход из строя i-го
конденсатора (i
= 1, 2, 3, 4),
- выход из строя i-го
конденсатора (i
= 1, 2, 3, 4),
 - выход из строя j-го
резистора (j
= 1, 2, 3, 4, 5). Электронная схема считается
исправной, если одновременно исправны
все транзисторы, не менее двух
конденсаторов и хотя бы один резистор.
Записать в алгебре событий: событие А
– схема исправна, и событие
- выход из строя j-го
резистора (j
= 1, 2, 3, 4, 5). Электронная схема считается
исправной, если одновременно исправны
все транзисторы, не менее двух
конденсаторов и хотя бы один резистор.
Записать в алгебре событий: событие А
– схема исправна, и событие
 .
.На книжном стеллаже хранятся 20 томов собрания сочинений Л.Н.Толстого. Библиотекарь наудачу выбирает несколько томов. Какова вероятность того, что первая книга будет том №2, вторая – том №4, третья – том №6, если: а) было взято 3 книги; б) взято 5 книг?
Прием больных проводят три врача – Иванов, Петров, Сидоров. Иванов ставит верный диагноз в 50%, Петров - в 70%, Сидоров - в 60% случаев. Найти вероятность постановки неверного диагноза больному, если он выбирает врача наудачу.
Рабочий обслуживает 3 станка, обрабатывающие однотипные детали. Производительность 1-го станка в три раза больше производительности 2-го и в полтора раза больше производительности 3-го. Процент брака для этих станков соответственно 2%, 4%, 1%. Наудачу взятая деталь, изготовленная этим рабочим, оказалась бракованной. Какова вероятность того, что взятая деталь изготовлена на 1-ом станке?
Вероятность содержания опасной концентрации фенола в каждой пробе речной воды равна 0,3. Исследуется 10 проб. Составить закон распределения числа проб с опасным содержанием фенола. Найти М(Х), D(X), σ(X) и F(X) этой случайной величины.
Дана функция распределения

случайной величины X. Найти: а) плотность распределения f(X); б) построить графики F(X) и f(X); в) М(Х); г) D(X); д) σ(X); е) .
Дана плотность распределения f(X) =
 непрерывной случайной величины Х.
Найти: а) параметр а;
б) функцию распределения F(X).
непрерывной случайной величины Х.
Найти: а) параметр а;
б) функцию распределения F(X).
