1. Пусть А, В, С – случайные события, выраженные подмножествами одного и того же множества элементарных событий. В алгебре событий запишите следующие события: Д - произошло два из данных событий; Е – произошли все три события; К – произошло не более двух из данных событий.

2. Буквальный замок содержит на общей оси 6 дисков, каждый из которых разделен на 8 секторов, отмеченных идущими подряд натуральными числами от 1 до 8. Замок открывается только в том случае, когда цифры образуют определенную комбинацию. Найти вероятность открыть замок, установив произвольную комбинацию цифр. Какова вероятность открыть замок, если известно, что кодовая комбинация не содержит цифр 2, 4 и цифры не повторяются?

3. На склад поступает продукция с трех фабрик. Продукция первой фабрики составляет 25%, второй - 30% и третьей - 45% от общего количества. Средний процент брака для первой фабрики равен 3%, для второй – 5%, для третьей – 2%. Найти вероятность того, что наудачу взятое изделие будет бракованным.

4. В саду растут три яблони. С первой яблони собрали 60% всего урожая яблок, со второй – 30%, с третьей – 10%. Известно, что для яблока с первой яблони вероятность быть червивым равна 0,05, со второй яблони – 0,09, а для третьей яблони – 0,2. Весь урожай был уложен в один контейнер. Наудачу взятое яблоко оказалось червивым. Вероятнее всего, с какой яблони оно было?

5. В партии из 6 деталей 4 стандартных. Наудачу отобраны 3 детали. Составить закон распределения Х – числа стандартных деталей среди отобранных. Найти М(Х), D(X), σ(X) и F(X) числа стандартных деталей среди отобранных.

6. Дана функция распределения 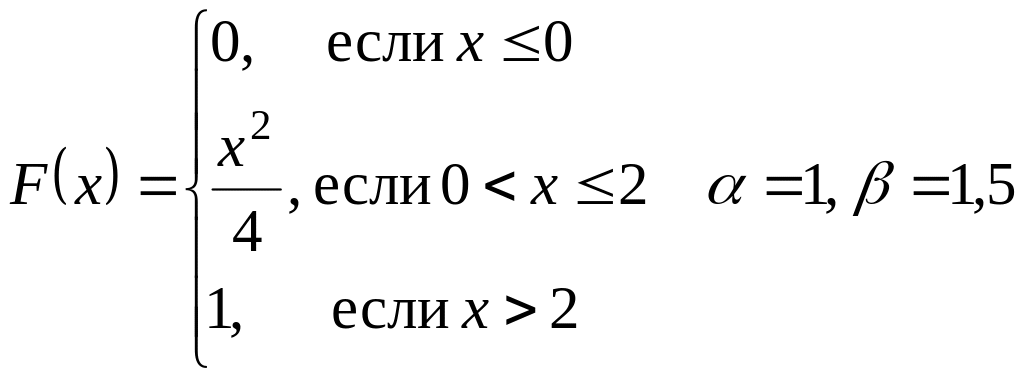случайной величины Х. Найти: а) плотность распределения f(X); б) построить графики F(X) и f(X); в) в) М(Х); г) D(X); д) σ(X); е) .

7. Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 22

1. Эксперимент состоит в бросании игральной кости. Пусть событие - появление четного числа очков; А₂ – появление двух очков; А₃ – появление четырех очков; А₄ – появление шести очков. Докажите на вероятностном языке и на теоретико-множественном языке, что:

а) ; б) Ø; в) А₁А₂=А₂.

2. Телефонный номер состоит из 7 цифр. Найти вероятность того, что все цифры номера различны. Какова вероятность угадать номер телефона, если известно, что среди его цифр нет 9 и 6?

3. Среди квартир, оборудованных сигнализацией, 30% оборудованы сигнализацией типа С-1, 50% - типа С-2, остальные – сигнализацией типа С-3. С-1 дает сбой с вероятностью 0,3, С-2 – с вероятностью 0,15, С-3 – с вероятностью 0,01. При попытке взлома сигнализация сработала. Найти вероятность того, что квартира была оборудована сигнализацией типа С-2.

4. В ящике имеется 5 синих и 50 красных шаров. Какова вероятность того, что при 10 независимых выборах с возвращением 3 раза будет выниматься синий шар?

5. Вероятность поражения цели при одном выстреле равна 0,4. Составить закон распределения числа выстрелов, производимых до первого поражения цели. Найти М(Х), D(X), σ(X) и F(X) этой случайной величины.

6. Дана функция распределения 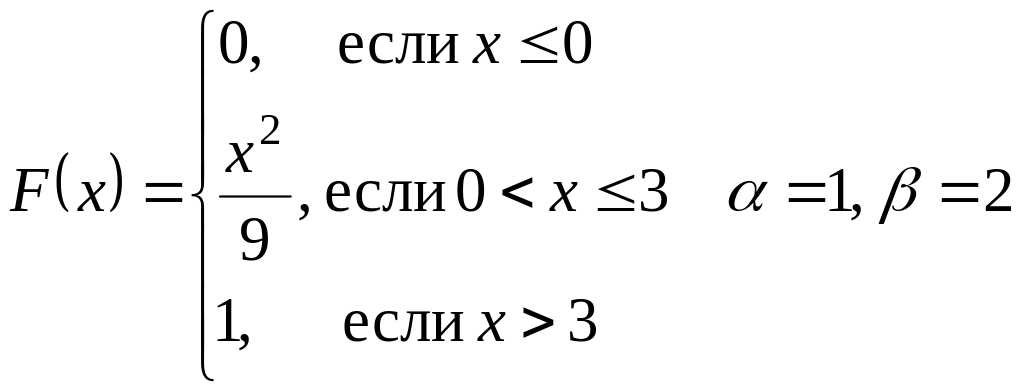случайной величины Х. Найти: а) плотность распределения f(X); б) построить графики F(X) и f(X); в) в) М(Х); г) D(X); д) σ(X); е) .

7. Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 23

1. Пусть А, В, С – три события, наблюдаемые в данном эксперименте. Выразите в алгебре событий А, В, С следующие события: Е₁ – из трех событий произошло хотя бы одно; Е₂ – из трех событий произошло ровно два; Е₃ – из трех событий не произойдет ни одного.

2. Для уменьшения общего количество игр 14 команд спортсменов по жребию разбиваются на две группы. Определить вероятность того, что две наиболее сильные команды окажутся в одной группе.

3. На сборку попадает детали, изготовление 3 станочниками. Первый станочник допускает 0,9 % брака, второй - 0,7%, третий - 0,5%. Найти вероятность попадания на сборку качественной детали, если первый станочник изготовил 400 деталей, второй - 700, третий - 900 деталей.

4. Пара одинаковых игральных костей бросается 7 раз. Какова вероятность того, что сумма очков равная 7 , выпадает дважды?

5. Радиосигнал передан 5 раз. Вероятность приема одного радио сигнала равна 0,7. Составить закон распределения случайной величины Х - числа принятых радиосигналов. Найти М(Х), D(X), σ(X) и F(X) этой случайной величины.

6. Дана функция распределения 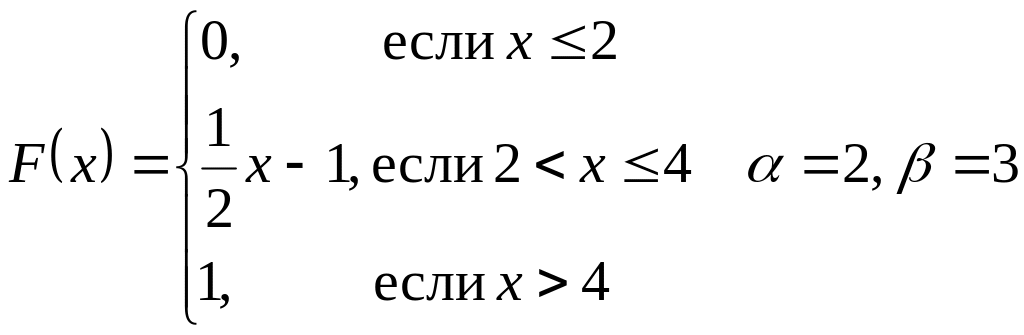случайной величины Х. Найти: а) плотность распределения f(X); б) построить графики F(X) и f(X); в) в) М(Х); г) D(X); д) σ(X); е) .

7. Дана плотность распределения непрерывной случайной величины х. Найти: а) параметр а; б) функцию распределения f(X). Вариант 24

1. Производится наблюдение за группой, состоящей из 4-х однородных объектов. Каждый из них за время наблюдения может быть обнаружен или не обнаружен. Рассматриваются события: А – обнаружен ровно один из 4-х объектов; В – обнаружен хотя бы один объект; С – обнаружено не менее двух объектов; Д - обнаружено ровно два объекта; Н – обнаружены все 4 объекта. В чем состоят события: а) АВ; б) ; в) ВН? Совпадают ли события ВС и Д?

2. Найти вероятность того, что четырехзначный номер случайно встретившейся автомашины: а) не содержит одинаковых цифр; б) не содержит цифру 2.

3. В тире имеются 3 ружья, вероятности попадания из которых соответственно равны 0,7, 0,8, 0,9. Стрелок взял одно из них наудачу и с первого раза поразил мишень. Какова вероятность того, что он стрелял из первого ружья?

4. Известно, что для одной волейбольной команды вероятность выиграть 3 партии из 5, и 2 партии из 4 равны 0,6. Найти вероятность выигрыша в одной партии.

5. Вероятность производства нестандартных деталей равна 0,15. Из партии контролер берет деталь и проверяет ее качество. Если она нестандартная, то испытания прекращаются и партия задерживается. Если деталь стандартная, то контролер берет следующую и т.д. Но всего он проверяет не более 4-х деталей. Составить закон распределения числа проверяемых деталей. Найти М(Х), D(X), σ(X) и F(X) этой случайной величины.

6. Дана функция распределения 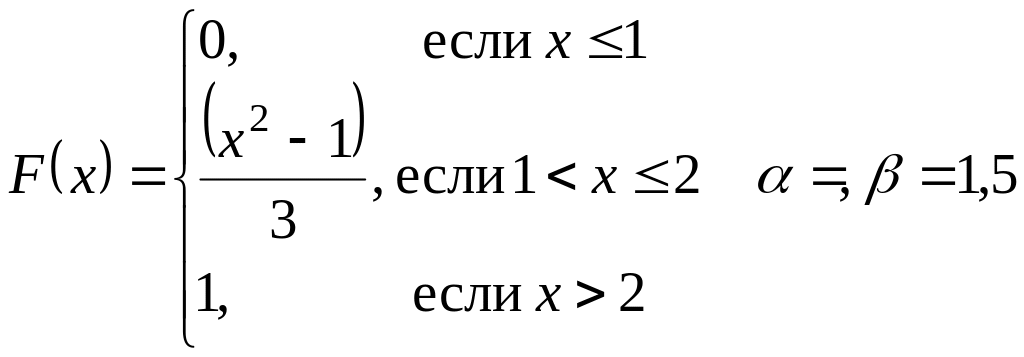случайной величины Х. Найти: а) плотность распределения f(X); б) построить графики F(X) и f(X); в) в) М(Х); г) D(X); д) σ(X); е) .

7. Дана плотность распределения непрерывной случайной величины Х

Найти: а) параметр а; б) функцию распределения F(X).